开锁次数的数学期望和方差

例  有n把看上去样子相同的钥匙，其中只有一把能把大门上的锁打开．用它们去试开门上的锁．设抽取钥匙是相互独立且等可能的．每把钥匙试开后不能放回．求试开次数的数学期望和方差．

分析：求时，由题知前次没打开，恰第k次打开．不过，一般我们应从简单的地方入手，如，发现规律后，推广到一般．

解：的可能取值为1，2，3，…，n．

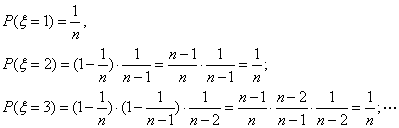
；所以的分布列为：

	1	2	…	k	…	n
			…		…

；

　　　　

　　

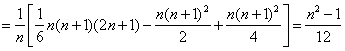
　　说明：复杂问题的简化处理，即从个数较小的看起，找出规律所在，进而推广到一般，方差的公式正确使用后，涉及一个数列求和问题，合理拆项，转化成熟悉的公式，是解决的关键．

次品个数的期望

例 　某批数量较大的商品的次品率是5％，从中任意地连续取出10件，为所含次品的个数，求．

分析：数量较大，意味着每次抽取时出现次品的概率都是0.05，可能取值是：0，1，2，…，10．10次抽取看成10次独立重复试验，所以抽到次品数服从二项分布，由公式可得解．

解：由题，，所以．

说明：随机变量的概率分布，是求其数学期望的关键．因此，入手时，决定取哪些值及其相应的概率，是重要的突破点．此题，应觉察到这是．

根据分布列求期望和方差

例　设是一个离散型随机变量，其分布列如下表，求值，并求．

	－1	0	1
P

分析：根据分布列的两个性质，先确定q的值，当分布列确定时，只须按定义代公式即可．

解： 离散型随机变量的分布满足

（1）

（2）

所以有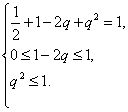解得　

故的分布列为

	－1	0	1
P

小结：解题时不能忽视条件时，，否则取了

的值后，辛辛苦苦计算得到的是两个毫无用处的计算．

产品中次品数分布列与期望值

例 　一批产品共100件，其中有10件是次品，为了检验其质量，从中以随机的方式选取5件，求在抽取的这5件产品中次品数分布列与期望值，并说明5件中有3件以上（包括3件）为次品的概率．（精确到0．001）

分析：根据题意确定随机变量及其取值，对于次品在3件以上的概率是3，4，5三种情况的和．

解：抽取的次品数是一个随机变量，设为，显然可以取从0到5的6个整数．

抽样中，如果恰巧有个（）次品，则其概率为

按照这个公式计算，并要求精确到0．001，则有

故的分布列为

	0	1	2	3	4	5
P	0.583	0.340	0.070	0.007	0	0

由分布列可知，

这就是说，所抽取的5件品中3件以上为次品的可能性很小，只有7％．

评定两保护区的管理水平

例　甲、乙两个野生动物保护区有相同的自然环境，且野生动物的种类和数量也大致相等．而两个保护区内每个季度发现违反保护条例的事件次数的分布列分别为：

甲保护区：

	0	1	2	3
	0.3	0.3	0.2	0.2

乙保护区：

	0	1	2
	0.1	0.5	0.4

试评定这两个保护区的管理水平．

分析：一是要比较一下甲、乙两个保护区内每季度发生的违规事件的次数的均值，即数学期望；二是要看发生违规事件次数的波动情况，即方差值的大小．（当然，亦可计算其标准差，同样说明道理．）

解：甲保护区的违规次数的数学期望和方差为：

乙保护区的违规次数的数学期望和方差为：

；

因为，所以两个保护区内每季度发生的违规平均次数是相同的，但乙保护区内的违规事件次数更集中和稳定，而甲保护区的违规事件次数相对分散和波动．

（标准差这两个值在科学计算器上容易获得，显然，）

说明：数学期望仅体现了随机变量取值的平均大小，但有时仅知道均值大小还是不够的，比如：两个随机变量的均值相等了（即数学期望值相等），这就还需要知道随机变量的取值如何在均值周期变化，即计算其方差（或是标准差）．方差大说明随机变量取值分散性大；方差小说明取值分散性小或者说取值比较集中、稳定．

射击练习中耗用子弹数的分布列、期望及方差

例　某射手进行射击练习，每射击5发子弹算一组，一旦命中就停止射击，并进入下一组的练习，否则一直打完5发子弹后才能进入下一组练习，若该射手在某组练习中射击命中一次，并且已知他射击一次的命中率为0.8，求在这一组练习中耗用子弹数的分布列，并求出的期望与方差（保留两位小数）．

分析：根据随机变量不同的取值确定对应的概率，在利用期望和方差的定义求解．

解： 该组练习耗用的子弹数为随机变量，可以取值为1，2，3，4，5．

＝1，表示一发即中，故概率为

＝2，表示第一发未中，第二发命中，故

＝3，表示第一、二发未中，第三发命中，故

＝4，表示第一、二、三发未中，第四发命中，故

＝5，表示第五发命中，故

因此，的分布列为

	1	2	3	4	5
P	0.8	0.16	0.032	0.0064	0.0016

说明：解决这类问题首先要确定随机变量的所有可能取值，然后再根据概率的知识求解对应的概率．

准备礼品的个数

例　某寻呼台共有客户3000人，若寻呼台准备了100份小礼品，邀请客户在指定时间来领取．假设任一客户去领奖的概率为4％．问：寻呼台能否向每一位顾客都发出奖邀请？若能使每一位领奖人都得到礼品，寻呼台至少应准备多少礼品？

分析：可能来多少人，是一个随机变量．而显然是服从二项分布的，用数学期望来反映平均来领奖人数，即能说明是否可行．

解：设来领奖的人数，所以，可见，所以，（人）（人）．

答：不能，寻呼台至少应准备120份礼品．

　　说明：“能”与“不能”是实际问题转到数学中来，即用数字来说明问题．数字期望反映了随机变量取值的平均水平．用它来刻画、比较和描述取值的平均情况，在一些实际问题中有重要的价值．因此，要想到用期望来解决这一问题．