3.2 简单的三角恒等变换
一、选择题：
1．已知cos（α+β）cos（α－β）=
，则cos2α－sin2β的值为（ ）
A．－
B．－ C． D．
2．在△ABC中，若sinAsinB=cos2
，则△ABC是（ ）
A．等边三角形 B．等腰三角形
C．不等边三角形 D．直角三角形
3．sinα+sinβ=
（cosβ－cosα），且α∈（0，π），β∈（0，π），则α－β等于（ ）
A．－
B．－
C． D．
4．已知sin（α+β）sin（β－α）=m，则cos2α－cos2β等于（ ）
A．－m B．m C．－4m D．4m
二、填空题
5．sin20°cos70°+sin10°sin50°=_________．
6．已知α－β=，且cosα+cosβ=，则cos（α+β）等于_________．
三、解答题
7．求证：4cos（60°－α）cosαcos（60°+α）=cos3α．
8．求值：tan9°+cot117°－tan243°－cot351°．
9．已知tan
，tanαtanβ=
，求cos（α－β）的值．
10．已知sinα+sinβ=
，cosα+cosβ=
，求tan（α+β）的值．
11．已知f（x）=－
+
，x∈（0，π）．
（1）将f（x）表示成cosx的多项式；
（2）求f（x）的最小值．
12．已知△ABC的三个内角A、B、C满足：A+C=2B，
，求cos
的值．
13． 已知sinA+sin3A+sin5A=a，cosA+cos3A+cos5A=b，
求证：（2cos2A+1）2=a2+b2．
14． 求证：cos2x+cos2（x+α）－2cosxcosαcos（x+α）=sin2α．
15． 求函数y=cos3x·cosx的最值．
参考答案
一、选择题
1．C 2． B 3． D 4． B
二、填空题
5．
6．－
三、解答题
7．证明：左边=2cosα［cos120°+cos（－2α）］
=2cosα（－
+cos2α）
=－cosα+2cosα·cos2α
=－cosα+cos3α+cosα
=cos3α=右边．
8．解：tan9°+cot117°－tan243°－cot351°
=tan9°－tan27°－cot27°+cot9°
=
=
=
=4．
9．解：∵tanαtanβ=
，
∴cos（α－β）=－
cos（α+β）．
又tan
，∴cos（α+β）=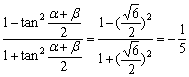
，
从而cos（α－β）=－×（－
）=．
10．解：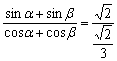
，由和差化积公式得
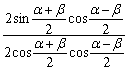=3，
∴tan
=3，从而tan（α+β）=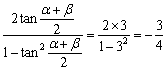
．
11．解：（1）f（x）=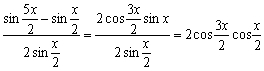
=cos2x+cosx=2cos2x+cosx－1．
（2）∵f（x）=2（cosx+）2－
，且－1≤cosx≤1，
∴当cosx=－时，f（x）取得最小值－．
12．分析：本小题考查三角函数的基础知识，利用三角公式进行恒等变形和运算的能力．
解：由题设条件知B=60°，A+C=120°，
∵－
=－2，
∴
=－2．
将上式化简为cosA+cosC=－2cosAcosC，
利用和差化积及积化和差公式，上式可化为
2cos
cos=－［cos（A+C）+cos（A－C）］，
将cos=cos60°=，cos（A+C）=cos120°=－代入上式得cos=
－cos（A－C），
将cos（A－C）=2cos2（）－1代入上式并整理得4cos2（）+2cos－3=0，
即［2cos－］［2cos+3］=0．
∵2cos+3≠0，∴2cos－=0．
∴cos=．
13．证明：由已知得
∴
两式平方相加得（2cos2A+1）2=a2+b2．
14．证明：左边=（1+cos2x）+［1+cos（2x+2α）］－2cosxcosαcos（x+α）
=1+［cos2x+cos（2x+2α）］－2cosxcosαcos（x+α）
=1+cos（2x+α）cosα－cosα［cos（2x+α）+cosα］
=1+cos（2x+α）cosα－cosαcos（2x+α）－cos2α
=1－cos2α=sin2α
=右边，
∴原不等式成立．
15．解：y=cos3x·cosx
=（cos4x+cos2x）
=（2cos22x－1+cos2x）
=cos22x+cos2x－
=（cos2x+）2－
．
∵cos2x∈［－1，1］，
∴当cos2x=－时，y取得最小值－；
当cos2x=1时，y取得最大值1．