高三数学综合检测题(必修一)
一、选择题
1.已知集合A={x![]() },B={
},B={![]() } C={
} C={![]() },又
},又![]() 则有()
则有()
A.(a+b)![]() A B.(a+b)
A B.(a+b) ![]() B
B
C.(a+b) ![]() C D. (a+b)
C D. (a+b) ![]() A、B、C任一个
A、B、C任一个
2.下列各式中,表示y是x的函数的有()
①y=x-(x-3); ②y=![]() +
+![]() ;
;
③y=![]() ④y=
④y=![]()
A.4个 B.3个 C.2个 D.1个
3.在映射![]() 中,
中,![]() ,且
,且![]() ,则与
,则与![]() 中的元素
中的元素![]() 对应的
对应的![]() 中的元素为()
中的元素为()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.下列结论中正确的个数是( )
①当a<0时,![]() =a3 ②
=a3 ②![]() =a ③函数y=
=a ③函数y=![]() -(3x-7)0的定义域是(2, +∞) ④若
-(3x-7)0的定义域是(2, +∞) ④若![]() ,则2a+b=1
,则2a+b=1
A.0 B.1 C.2 D.3
5.已知函数![]() 的两个零点是2和3,则函数
的两个零点是2和3,则函数![]() 的零点是()
的零点是()
A.![]() 和
和![]() B.
B.![]() 和
和![]() C.
C.![]() 和
和![]() D.
D.![]() 和
和![]()
6.若![]() ,定义
,定义![]() ,如
,如![]() ,则函数
,则函数![]() 的奇偶性为( )
的奇偶性为( )
A是奇函数不是偶函数 B是偶函数不是奇函数
C既是奇函数又是偶函数 D非奇非偶函数
7.已知![]() 为偶函数,且
为偶函数,且![]() ,当
,当![]() 时,
时,![]() ,若
,若![]() ,
,![]() ,则
,则![]()
(A)2006
(B)4
(C)![]() (D)
(D)![]()
8.若函数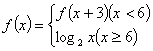 ,则
,则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9、设![]() ,若
,若![]() ,且
,且 ![]() >
>![]() ,则下列结论中必成立的是( )
,则下列结论中必成立的是( )
A.![]() >
>![]() B.
B.![]() >0 C.
>0 C.![]() <
<![]() D.
D.![]() >
>![]()
10.在股票买卖过程中,经常用到两种曲线,一种是即时价格曲线y=f(x),另一种是平均价格曲线y=g(x)(如f(2)=3是指开始买卖后二个小时的即时价格为3元;g(2)=3表示二个小时内的平均价格为3元),下图给出的四个图像,其中实线表示y=f(x),虚线表示y=g(x),其中可能正确的是 ()
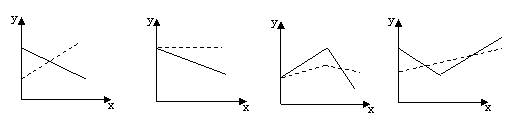 |
A B C D
11.函数![]() 的零点一定位于的区间是( )
的零点一定位于的区间是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.已知函数![]() ,则
,则![]() 与
与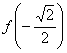 的大小是( )
的大小是( )
A.![]()
![]()
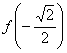 B.
B.![]()
![]()
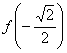
C.![]() =
=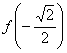 D.不能确定
D.不能确定
二.填空题:
13.函数![]() ,在
,在![]() 上的最大值与最小值之和为
上的最大值与最小值之和为![]() ,则
,则![]() 的值为________________________.
的值为________________________.
14. 已知函数![]() 满足对任意的
满足对任意的![]() 都有
都有![]() 成立,则
成立,则![]() = .
= .
15.若二次函数![]() 和
和![]() 使得
使得![]() 在
在![]() 上是增函数的条件是__________________.
上是增函数的条件是__________________.
16.函数![]() 在
在![]() 上是减函数,则实数
上是减函数,则实数![]() 的取值范围是____________________.
的取值范围是____________________.
三.解答题
17.已知函数![]() 且
且![]() ,
,
(1)求![]() 的值;
的值;
(2)判定![]() 的奇偶性;
的奇偶性;
(3)判断![]() 在
在![]() 上的单调性,并给予证明.
上的单调性,并给予证明.
18.集合![]() 是由适合以下性质的函数组成:对于任意
是由适合以下性质的函数组成:对于任意![]() ,
,![]() ,且
,且![]() 在
在![]() 上是增函数,
上是增函数,
(1)试判断![]() 及
及![]() 是否在集合
是否在集合![]() 中,若不在
中,若不在![]() 中,试说明理由;
中,试说明理由;
(2)对于(1)中你认为集合![]() 中的函数
中的函数![]() ,不等式
,不等式![]()
![]() 是否对任意
是否对任意![]()
![]() 恒成立,试证明你的结论.
恒成立,试证明你的结论.
19.已知![]() 是偶函数.
是偶函数.
(1)求![]() 的值;
的值;
(2)证明:对任意实数![]() ,函数
,函数![]() 的图象与直线
的图象与直线![]() 最多只有一个交点.
最多只有一个交点.
20.已知函数![]() .
.
(1)判断函数![]() 的奇偶性;
的奇偶性;
(2)判断函数![]() 在定义域内是增函数还是减函数?请说明理由;
在定义域内是增函数还是减函数?请说明理由;
(3)已知![]() ,解关于
,解关于![]() 不等式:
不等式: ![]() .
.
21.某租赁公司拥有汽车100辆. 当每辆车的月租金为3000元时,可全部租出. 当每辆车的月租金每增加50元时,未租出的车将会增加一辆. 租出的车每辆每月需要维护费200元.
(Ⅰ)当每辆车的月租金定为3600元时,能租出多少辆车?
(Ⅱ)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少元?
22.如果函数![]() 的定义域为
的定义域为![]() ,对任意实数
,对任意实数![]() 满足
满足![]() .
.
(1)设![]() ,试求
,试求![]() ;(2)设当
;(2)设当![]() 时,
时,![]() ,试解不等式
,试解不等式![]() .
.
高三数学必修一综合参考答案
1.答案:B
2.答案:C 提示: ①③表示y是x的函数;在②中由![]() 知x∈
知x∈![]() ,因为函数定义域不能是空集,所以②不表示y是x的函数;在④中若x=0,则对应的y的值不唯一,所以④不表示y是x的函数.
,因为函数定义域不能是空集,所以②不表示y是x的函数;在④中若x=0,则对应的y的值不唯一,所以④不表示y是x的函数.
3.答案:A
4.答案:B 提示:取a=-2,可验证①不正确;
当n为奇数时,②不正确;
③y=![]() -(3x-7)0的定义域应是[2,
-(3x-7)0的定义域应是[2,![]() ]∪(
]∪(![]() ,+∞);
,+∞);
④由100a=5,得102a=5. (1) 又10b=2, (2)
(1)×(2)得102a+b=10.
∴2a+b=1,此命题正确.
5.答案:D 6.答案: B. 7.答案:C 8.答案:C 9.答案:D
10.答案:C 11.答案:B 12.答案:A 13.答案:![]()
14.答案:7 提示:分别令x=0,![]() ,
,![]() ,
,![]() ,
,
由f(![]() +x)+f(
+x)+f(![]() -x)=2,
-x)=2,
得f(![]() )+f(
)+f(![]() )=2,f(
)=2,f(![]() )+f(
)+f(![]() )=2,f(
)=2,f(![]() )+f(
)+f(![]() )=2,f(
)=2,f(![]() )+f(
)+f(![]() )=2,
)=2,
∴f(![]() )+f(
)+f(![]() )+…+f(
)+…+f(![]() )=7.
)=7.
15.答案:![]() 且
且![]() 提示:
提示:![]() ,欲使
,欲使![]() 在
在![]() 上是增函数,必须使其为一次函数,且一次项系数大于0.
上是增函数,必须使其为一次函数,且一次项系数大于0.
16.答案:![]()
17.解:(1)因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
(2)因为![]() 的定义域为
的定义域为![]() ,又
,又![]() ,所以
,所以![]() 是奇函数.
是奇函数.
(3)设![]() ,则
,则
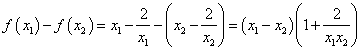 ,因为
,因为![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上为单调增函数.
上为单调增函数.
18.解:(1)当![]() 时,
时,![]()
![]() ,所以
,所以![]() ,又
,又![]() 值域为
值域为![]() ,所以
,所以![]() ;
;
当![]() 时
时![]() 为增函数,所以
为增函数,所以![]() .
.
(2)
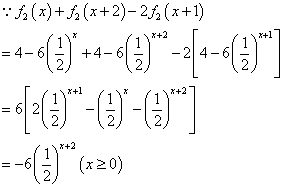
![]() 对任意
对任意![]() 不等式
不等式![]() 总成立,
总成立,
19.(1)解:由![]() ,得
,得![]() .
.
(2)证明:由(1)得![]() ,令
,令![]() ,得
,得![]() ,
,
假设方程有两个不等的实数根,则![]() ①,
①,![]() ②.
②.
两式相减得![]() ,
,
因为![]() ,所以
,所以![]() ,代入①或②不成立,假设错误,命题成立.
,代入①或②不成立,假设错误,命题成立.
20.解: (1)由![]() 得函数
得函数![]() 的定义域是
的定义域是![]() . 又
. 又![]() .
.
所以函数![]() 是奇函数.
是奇函数.
(2)设![]() ,则
,则
![]()
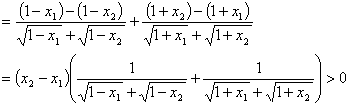
所以函数![]() 在定义域
在定义域![]() 上是单调减函数.
上是单调减函数.
注:也可以用导数知识判断.
(3)因![]() ,所以,不等式等价为
,所以,不等式等价为
![]() ,
,
考虑到![]() 在定义域
在定义域![]() 上是单调减函数,所以又化为
上是单调减函数,所以又化为
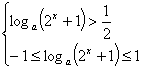 ,即
,即![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,
,
![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ,这与
,这与![]() 矛盾.
矛盾.
故当![]() 时,解集为
时,解集为![]() ;
;
当![]() 时,解集为空集.
时,解集为空集.
21.解:(Ⅰ)当每辆车的月租金定为3600元时,未租出的车辆数为![]() ,
,
所以这时租出了88辆车.
(Ⅱ)设每辆车的月租金定为x元,则租赁公司的月收益为
![]() ,
,
整理得
![]() .
.
所以,当x=4100时,![]() 最大,最大值为
最大,最大值为![]() ,
,
即当每辆车的月租金定为4100元时,租赁公司的月收益最大,最大月收益为304200元.
22. 解: (1)因为![]() ,所以
,所以![]() ,
,
于是![]() .
.
(2)对任意的![]() ,
,![]() .
.
假设存在![]() ,使
,使![]() ,
,
则取![]() ,有
,有![]() ,
,
这与已知矛盾,则![]() .于是对任意
.于是对任意![]() ,必有
,必有![]() .
.
∵![]() ,∴
,∴![]() .
.
设![]() ,则
,则![]() .
.
又∵![]() ,∴
,∴![]() ,
,
∴![]() 为减函数.不等式等价于
为减函数.不等式等价于![]() ,
,
∴![]() .
.