2.3 平面向量的基本定理及坐标表示
一、选择题
1、若向量![]() =
(1,1),
=
(1,1), ![]() = (1,-1),
= (1,-1), ![]() =(-1,2),则
=(-1,2),则 ![]() 等于( )
等于( )
A、![]()
![]() +
+![]()
![]() B、
B、![]()
![]()
![]()
![]() C、
C、![]()
![]()
![]()
![]() D、
D、![]()
![]() +
+ ![]()
![]()
2、已知,A(2,3),B(-4,5),则与![]() 共线的单位向量是 ( )
共线的单位向量是 ( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
3、已知![]() 垂直时k值为 ( )
垂直时k值为 ( )
A、17 B、
4、已知向量![]() =(2,1),
=(2,1),![]() =(1,7),
=(1,7),![]() =(5,1),设X是直线OP上的一点(O为坐标原点),那么
=(5,1),设X是直线OP上的一点(O为坐标原点),那么![]() 的最小值是
( )
的最小值是
( )
A、-16
B、
5、若向量![]() 分别是直线ax+(b-a)y-a=0和ax+4by+b=0的方向向量,则 a, b的值分别可以是
( )
分别是直线ax+(b-a)y-a=0和ax+4by+b=0的方向向量,则 a, b的值分别可以是
( )
A、 -1 ,2 B、 -2 ,
6、若向量a=(cos![]() ,sin
,sin![]() ),b=(cos
),b=(cos![]() ,sin
,sin![]() ),则a与b一定满足
( )
),则a与b一定满足
( )
A、a与b的夹角等于![]() -
-![]() B、(a+b)⊥(a-b)
B、(a+b)⊥(a-b)
C、a∥b D、a⊥b
7、设![]() 分别是
分别是![]() 轴,
轴,![]() 轴正方向上的单位向量,
轴正方向上的单位向量,![]() ,
,![]() 。若用来表示
。若用来表示![]() 与
与![]() 的夹角,则等于 ( )
的夹角,则等于 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
8、设![]() ,已知两个向量
,已知两个向量![]() ,
,![]() ,则向量
,则向量![]() 长度的最大值是( )
长度的最大值是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、
二、填空题
9、已知点A(2,0),B(4,0),动点P在抛物线y2=-4x运动,则使![]() 取得最小值的点P的坐标是
、
取得最小值的点P的坐标是
、
10、把函数![]() 的图象,按向量
的图象,按向量![]() (m>0)平移后所得的图象关于
(m>0)平移后所得的图象关于![]() 轴对称,则m的最小正值为__________________、
轴对称,则m的最小正值为__________________、
11、已知向量![]() 、
、
三、解答题
12、求点A(-3,5)关于点P(-1,2)的对称点![]() 、
、
13、平面直角坐标系有点![]()
(1)求向量![]() 的夹角
的夹角![]() 的余弦用x表示的函数
的余弦用x表示的函数![]() ;
;
(2)求![]() 的最值、
的最值、
14、设![]()
![]() 其中x∈[0,
其中x∈[0,![]() ]、
]、
(1)求f(x)=![]() 的最大值和最小值;
的最大值和最小值;
(2)当 ![]() ⊥
⊥![]() ,求
,求![]() 、
、
15、已知定点![]() 、
、![]() 、
、![]() ,动点
,动点![]() 满足:
满足:
![]() 、
、
(1)求动点![]() 的轨迹方程,并说明方程表示的图形;
的轨迹方程,并说明方程表示的图形;
(2)当![]() 时,求
时,求![]() 的最大值和最小值、
的最大值和最小值、
参考答案
一、选择题
1、B;2、B;3、C;4、B;5、D;6、B;7、D;8、C
二、填空题
9、(0,0)
10、![]()
11、4
三、解答题
12、解:设![]() (x,y),则有
(x,y),则有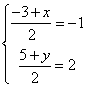 ,解得
,解得![]() 、所以
、所以![]() (1,-1)。
(1,-1)。
13、解:(1)![]() (2)
(2)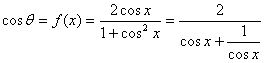 且
且![]() ,
,![]()
![]()
![]()
![]()
![]()
14、解:⑴f(x)=![]() = -2sinxcosx+cos2x=
= -2sinxcosx+cos2x=![]() 、
、
∵0≤x≤![]() , ∴
, ∴![]() ≤2x+
≤2x+![]() ≤
≤![]() 、
、
∴当2x+![]() =
=![]() ,即x=0时,f(x)max=1;
,即x=0时,f(x)max=1;
当2x+![]() =π,即x=
=π,即x=![]() π时,f(x)min= -
π时,f(x)min= -![]() 、
、
⑵![]() 即f(x)=0,2x+
即f(x)=0,2x+![]() =
=![]() ,∴x=
,∴x=![]() 、
、
此时![]()
![]()
=![]()
=![]()
=![]()
=![]() 、
、
15、解:( 1 ) 设动点![]() 的坐标为
的坐标为![]() ,
,
则![]() ,
,![]() ,
,![]() 、
、
∵![]() ,∴
,∴![]() ,
,
即 ![]() 。
。
若![]() ,则方程为
,则方程为![]() ,表示过点
,表示过点![]() 且平行于
且平行于![]() 轴的直线、
轴的直线、
若![]() ,则方程为
,则方程为![]() ,表示以
,表示以![]() 为圆心,以为半径
为圆心,以为半径
![]() 的圆、
的圆、
(
2 ) 当![]() 时,方程化为
时,方程化为![]() 、
、![]()
∴![]() 、
、
又∵![]() ,∴ 令
,∴ 令![]() ,则
,则
![]()
∴当![]() 时,
时,![]() 的最大值为
的最大值为![]() ,当
,当![]() 时,最小值为
时,最小值为![]() 。
。