2.3　直线、平面垂直的判定及其性质

一、选择题

1、P是△ABC所在平面α外一点，且P到△ABC三边的距离相等，PO⊥α于O，O在△ABC内，则O是△ABC的　　　　　　　　　　　　　　　　　　　　　　　　　 （　　　）

A、外心　　　　　　　　 B、内心　　　　　　　　C、重心　　　　　　　 D、垂心

2、正方体ABCD-A₁B­₁C₁D₁中与AD₁垂直的平面是　　　　　　　　　　　　　　 （　 ）

A、平面DD₁C₁CB、平面A₁DB₁　　　 　　　

C、平面A₁B₁C₁D₁　　　 D、平面A₁DB

3、已知平面α外的直线b垂直于α内的二条直线，有以下结论：1b一定不垂直于α；2b可能垂直于平面α；3b一定不平行于平面α，其中正确的结论有

A、0个　　　　　　　　　B、1个　　　　　　　　 C、2个　　　　　　　　D、3个

4、直线l与平面a内的两条直线都垂直，则直线l与平面a的位置关系是　 　　（　 ）

A、平行　 B、垂直　C、在平面a内　　　D、无法确定

5、下面各命题中正确的是　　　　　　　　　　　 　　　　　 （　 ）

A、直线a，b异面，aÌa，bÌb，则a∥b；

B、直线a∥b，aÌa，bÌb，则a∥b；

C、直线a⊥b，a⊥a，b⊥b，则a⊥b；

D、直线aÌa，bÌb，a∥b，则a，b异面.

6、对于已知直线a，如果直线b同时满足下列三个条件：

①与a是异面直线；②与a所成的角为定值θ；③与a距离为定值d.

那么这样的直线b有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　 ）

A、1条　　　　 B、2条 　　　C、3条　　　　　　 D、无数条

7、直线与平面a内的两条直线都垂直，则直线与平面a的位置关系是　 　　　 （　 ）

A、平行　　　 B、垂直　　　　 C、在平面a内　 D、无法确定

8、对于已知直线a，如果直线b同时满足下列三个条件：

①与a是异面直线；②与a所成的角为定值θ；③与a距离为定值d

那么这样的直线b有　　　　　　　　　　　　　　　　　　　  　　　　（　 ）

A、1条　　　　 B、2条　　　　  C、3条　　　　D、无数条

二、填空题

9、从点O出发的不共面的3条射线OA、OB、OC中，如果∠AOB＝∠AOC，则OA在平面BOC上的射影落在∠BOC的________．

10、若∠AOB在平面内，OC是的斜线，∠AOC＝∠BOC＝60°，OC与成45°角，则∠AOB＝________．

11、点A、B∈平面，点P，线段AP、PB在内的射影长分别为3和5，则线段AB的最大值是________，最小值是________．

12、PD垂直于正六边形ABCDEF，若正六边形边长为a，PD＝a，则点P到BC的距离为________．

13、边长为a的正四面体A—BCD，M是棱AB的中点，则CM与底面BCD所成的角的正弦值是________．

三、解答题

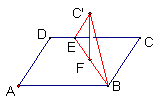14、已知矩形ABCD的边长AB＝6cm，BC＝4cm，在CD上截取CE＝4cm，以BE为棱将矩形折起，使△BC′E的高C′F⊥平面ABED，求：

（1）点C′到平面ABED的距离；

（2）C′到边AB的距离；

（3）C′到AD的距离．

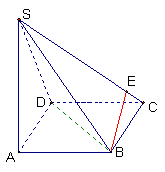
15、如图，已知ABCD是矩形，SA⊥平面ABCD，E是SC上一点．

求证：BE不可能垂直于平面SCD．

参考答案

一、选择题

1、B；2、B；3、B；4、D；5、C；6、D；7、D；8、D

二、填空题

9、平分线上

10、90°

11、8　　 2

12、a

13、

三、解答题

14、解：（1）作FH⊥AB于H，作FG⊥AD于G，

则C′H⊥AB，,可算得BE=4cm，HB=2cm，

∴到平面ABED的距离为cm

_⑵到平面AB的距离为cm

_⑶到平面AD的距离为cm

15、解：用到反证法，假设BE⊥平面SCD，

∵ AB∥CD；∴AB⊥BE．

∴ AB⊥SB，这与Rt△SAB中∠SBA为锐角矛盾．

∴ BE不可能垂直于平面SCD