3.1 两角和与差的正弦、余弦正切公式
一、选择题:
1.sin![]() cos
cos![]() -cos
-cos![]() sin
sin![]() 的值是(
)
的值是(
)
A.-![]() B.
B.![]() C.-sin
C.-sin![]() D.sin
D.sin![]()
2.若sin(α+β)cosβ-cos(α+β)sinβ=0,则sin(α+2β)+sin(α-2β)等于( )
A.1 B.-1 C.0 D.±1
二、解答题
3.已知![]() <α<
<α<![]() ,0<β<
,0<β<![]() ,cos(
,cos(![]() +α)=-
+α)=-![]() ,sin(
,sin(![]() +β)=
+β)=![]() ,求sin(α+β)的值.
,求sin(α+β)的值.
4.已知非零常数a、b满足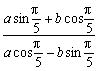 =tan
=tan![]() ,求
,求![]() .
.
5.已知0<α<![]() ,sin(
,sin(![]() -α)=
-α)=![]() ,求
,求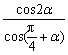 的值.
的值.
6.已知sin(α+β)=![]() ,sin(α-β)=
,sin(α-β)=![]() ,求
,求![]() 的值.
的值.
7.已知A、B、C是△ABC的三个内角且lgsinA-lgsinB-lgcosC=lg2.试判断此三角形的形状特征.
8.化简![]() .
.
9. 求值:(1)sin75°;
(2)sin13°cos17°+cos13°sin17°.
10. 求sin![]() cos
cos![]() -sin
-sin![]() sin
sin![]() 的值.
的值.
11. 在足球比赛中,甲方边锋从乙方半场带球过人沿直线前进(如下图),试问甲方边锋在何处射门命中乙方球门的可能性最大?(设乙方球门两个端点分别为A、B)

12. 已知![]() <α<β<
<α<β<![]() ,cos(α-β)=
,cos(α-β)=![]() ,sin(α+β)=-
,sin(α+β)=-![]() ,求sin2α的值.
,求sin2α的值.
13. 证明sin(α+β)sin(α-β)=sin2α-sin2β,并利用该式计算sin220°+ sin80°·sin40°的值.
14. 化简:[2sin50°+sin10°(1+![]() tan10°)]·
tan10°)]·![]() .
.
15. 已知函数y=sinx+cosx+2sinxcosx+2,
(1)若x∈R,求函数的最大值和最小值;
(2)若x∈[0,![]() ],求函数的最大值和最小值.
],求函数的最大值和最小值.
参考答案
1.B 2. C
3.解:∵![]() <α<
<α<![]() ,
,
∴![]() <
<![]() +α<π.
+α<π.
又cos(![]() +α)=-
+α)=-![]() ,
,
∴sin(![]() +α)=
+α)=![]() .
.
∵0<β<![]() ,
,
∴![]() <
<![]() +β<π.
+β<π.
又sin(![]() +β)=
+β)=![]() ,
,
∴cos(![]() +β)=-
+β)=-![]() ,
,
∴sin(α+β)=-sin[π+(α+β)]=-sin[(![]() +α)+(
+α)+(![]() +β)]
+β)]
=-[sin(![]() +α)cos(
+α)cos(![]() +β)+cos(
+β)+cos(![]() +α)sin(
+α)sin(![]() +β)]
+β)]
=-[![]() ×(-
×(-![]() )-
)-![]() ×
×![]() ]=
]=![]() .
.
4.分析:这道题看起来复杂,但是只要能从式子中整理出![]() ,用
,用![]() 、
、![]() 的三角函数表示出来,再利用两角和与差的正、余弦公式计算即可.
的三角函数表示出来,再利用两角和与差的正、余弦公式计算即可.
解:由于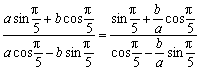 ,则
,则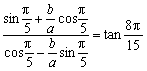 .
.
整理,有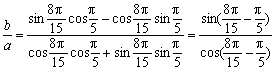 =tan
=tan![]() =
=![]() .
.
5.分析:这道题的选题意图是考查两角和与差的正、余弦公式和诱导公式的综合运用以及变角技巧.解题过程中,需要注意到(![]() +α)+(
+α)+(![]() -α)=
-α)=![]() ,并且(
,并且(![]() +α)-(
+α)-(![]() -α)=2α.
-α)=2α.
解:cos(![]() +α)=cos[
+α)=cos[![]() -(
-(![]() -α)]=sin(
-α)]=sin(![]() -α)=
-α)=![]() ,
,
又由于0<α<![]() ,
,
则0<![]() -α<
-α<![]() ,
,![]() <
<![]() +α<
+α<![]() .
.
所以cos(![]() -α)=
-α)=![]() ,
,
sin![]() .
.
因此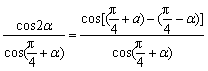
=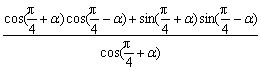
=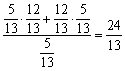 .
.
6.分析:当题中有异角、异名时,常需化角、化名,有时将单角转化为复角(和或差).本题是将复角化成单角,正(余)切和正(余)弦常常互化.
欲求![]() 的值,需化切为弦,即
的值,需化切为弦,即![]() ,可再求sinαcosβ、cosαsinβ的值.
,可再求sinαcosβ、cosαsinβ的值.
解:∵sin(α+β)=![]() ,∴sinαcosβ+cosαsinβ=
,∴sinαcosβ+cosαsinβ=![]() . ①
. ①
∵sin(α-β)=![]() ,∴sinαcosβ-cosαsinβ=
,∴sinαcosβ-cosαsinβ=![]() . ②
. ②
由(①+②)÷(①-②)得![]() =-17.
=-17.
7.分析:从角与角的关系探究三角函数间的关系;反之,利用三角函数间的关系去判断角的大小及关系,这是常用的基本方法.可以先化去对数符号,将对数式转化为有理式,然后再考察A、B、C的关系及大小,据此判明形状特征.
解:由于lgsinA-lgsinB-lgcosC=lg2,
可得lgsinA=lg2+lgsinB+lgcosC,
即lgsinA=lg2sinBcosC,
sinA=2sinBcosC.
根据内角和定理,A+B+C=π,
∴A=π-(B+C).
∴sin(B+C)=2sinBcosC,
即sinBcosC+cosBsinC=2sinBcosC.
移项化为sinCcosB-sinBcosC=0,
即sin(B-C)=0.
∴在△ABC中,C=B.
∴△ABC为等腰三角形.
8.分析:这道题要观察出7°+8°=15°,解题过程中还需要应用两角和与差的正弦、余弦公式.
解:![]()
=![]()
=![]()
=![]()
=2-![]() .
.
9.解:(1)原式=sin(30°+45°)= sin30°cos45°+cos30°sin45°=![]() ·
·![]() +
+![]() ·
·![]() =
=
![]() .
.
(2)原式= sin(13°+17°)=sin30°=![]() .
.
10.解:观察分析这些角的联系,会发现![]() =
=![]() -
-![]() .
.
sin![]() cos
cos![]() -sin
-sin![]() sin
sin![]()
=sin![]() cos
cos![]() -sin(
-sin(![]() -
-![]() )sin
)sin![]()
=sin![]() cos
cos![]() -cos
-cos![]() sin
sin![]()
=sin(![]() -
-![]() )
)
=sin![]()
=![]() .
.
11.解:设边锋为C,C到足球门AB所在的直线的距离为CO=x,OB=b,OA=a(a>b>0,a、b为定值),∠ACO=α,∠BCO=β,∠ACB=α-β=γ(0<γ<![]() ),
),
则tanα=![]() ,tanβ=
,tanβ=![]() (x>0,
(x>0,![]() >0).
>0).
所以tanγ=tan(α-β)=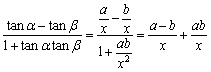 ≤
≤![]() .
.
当且仅当x=![]() ,即x=
,即x=![]() 时,上述等式成立.又0<γ<
时,上述等式成立.又0<γ<![]() ,tanγ为增函数,所以当x=
,tanγ为增函数,所以当x=![]() 时,tanγ达到最大,从而∠ACB达到最大值arctan
时,tanγ达到最大,从而∠ACB达到最大值arctan![]() .
.
所以边锋C距球门AB所在的直线距离为![]() 时,射门可以命中球门的可能性最大.
时,射门可以命中球门的可能性最大.
12.解:此题考查“变角”的技巧.由分析可知2α=(α-β)+(α+β).
由于![]() <α<β<
<α<β<![]() ,可得到π<α+β<
,可得到π<α+β<![]() ,0<α-β<
,0<α-β<![]() .
.
∴cos(α+β)=-![]() ,sin(α-β)=
,sin(α-β)=![]() .
.
∴sin2α=sin[(α+β)+(α-β)]
=sin(α+β)cos(α-β)+cos(α+β)sin(α-β)
=(-![]() )·
)·![]() +(-
+(-![]() )·
)·![]()
=-![]() .
.
13.证明:sin(α+β)sin(α-β)=(sinαcosβ+cosαsinβ)(sinαcosβ-cosαsinβ)
=sin2αcos2β-cos2αsin2β
=sin2α(1-sin2β)-(1-sin2α)sin2β
=sin2α-sin2αsin2β-sin2β+sin2αsin2β
=sin2α-sin2β,
所以左边=右边,原题得证.
计算sin220°+sin80°·sin40°,需要先观察角之间的关系.经观察可知80°=60°+ 20°,40°=60°-20°,
所以sin220°+sin80°·sin40°=sin220°+sin(60°+20°)·sin(60°-20°)
=sin220°+sin260°-sin220°
=sin260°
=![]() .
.
分析:此题目要灵活运用“化切为弦”的方法,再利用两角和与差的三角函数关系式整理化简.
14.解:原式=[2sin50°+sin10°(1+![]() tan10°)]·
tan10°)]·![]()
=[2sin50°+sin10°(1+![]()
![]() )]·
)]·![]()
=[2sin50°+sin10°(![]() )]·
)]·![]()
=(2sin50°+2sin10°·![]() )·
)·![]() cos10°
cos10°
=2![]() (sin50°cos10°+sin10°·cos50°)
(sin50°cos10°+sin10°·cos50°)
=2![]() sin60°=
sin60°=![]() .
.
15.解:(1)设t=sinx+cosx=![]() sin(x+
sin(x+![]() )∈[-
)∈[-![]() ,
,![]() ],
],
则t2=1+2sinxcosx.
∴2sinxcosx=t2-1.
∴y=t2+t+1=(t+![]() )2+
)2+![]() ∈[
∈[![]() ,3+
,3+![]() ]
]
∴ymax=3+![]() ,ymin=
,ymin=![]() .
.
(2)若x∈[0,![]() ],则t∈[1,
],则t∈[1,![]() ].
].
∴y∈[3,3+![]() ],
],
即ymax=3+![]() ymin=3.
ymin=3.
