3.1　两角和与差的正弦余弦正切公式

一、选择题：

1．Sin165º等于　　　（　　 ）

A．　　 B．　 C．　 D．　

2．Sin14ºcos16º+sin76ºcos74º的值是（　　　）

A．　 B．　 C．　D．-

3．sin-cos的值是．　　　　　　　　 （　　 ）

A．0　　　　B． —　　 C． 　　D．　2 sin

4.△ABC中，若2cosBsinA=sinC　则△ABC的形状一定是（　　）

A．等腰直角三角形　　B．直角三角形 C．等腰三角形　　　 D．等边三角形

5．函数y=sinx+cosx+2的最小值是　（　　　）

A．2-　 B．2+　　C．0　　D．1

二、填空题．

6．=__________________________．

7．如果cos= -　，那么 cos=________．

8．已知为锐角，且cos=　 cos = -,  则cos=_________．

9．tan20º+tan40º+tan20ºtan40º的值是____________．

10．函数y=cosx+cos(x+)的最大值是__________．

三、解答题．

11．若是同一三角形的两个内角，cos= -  ,cos(=-.求cot的值．

12．在△ABC中，若cosA=　,cosB= , 试判断三角形的形状．

13．A、B、C是一条直路上的三点，AB与BC各等于1 km.从三点分别遥望塔M，在A处见塔在东北方向，在B处见塔在正东方向，在C处见塔在南偏东60°，求塔与路的最短距离.

14． 求tan15°、tan75°的值.

15．求的值.

参考答案

一、选择题：

1.D　2.B　 3.B　4.C　 5.A

二、填空题：

6：　7：　 8：　 9：　 10：

三、解答题：

11、　解：∵是同一三角形的两个内角　　∴　 0<<

∵cos(=-　　 ∴sin(==

∵cos= - 　　　　　∴sin==

∴sin= sin(=sin(cos- cos(sin=

∴cos==

∴tan==

∴cot=

12、解：∵在△ABC中，若cosA=>0　,cosB=>0　 ∴A，B为锐角

sinA==　　  sinB==

∵ cosC=cos[-(A+B)]=-cos(A+B)=-（cosAcosB-sinAsinB）= < 0

∴< C <　 即C为钝角

∴△ABC为钝角三角形.

13．解：如下图，设塔到路的距离MD为x km，∠BMD=θ，

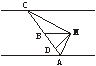
则∠CMD=θ+30°，∠AMD=45°－θ，AB=BD+DA=xtan（45°－θ）+xtanθ，BC=CD－BD=xtan（30°+θ）－xtanθ.

因为AB=BC=1，

所以xtan（45°－θ）+xtanθ=xtan（30°+θ）－xtanθ=1.

解得x=.

所以，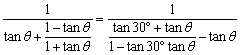

即.

解得tanθ=.

所以x=.

因此塔到路的最短距离为 km.

14．解：tan15°=tan（45°－30°）=.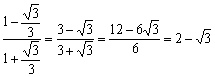

tan75°=tan（45°+30°）=.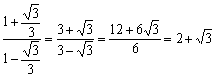

15．解：此题是着重考查学生是否灵活掌握弦与切之间的相互转换原则，即化弦（切）为切（弦），并且要注意到正切三角函数值里的一个特殊数字“1”，即tan45°=1.

把原式分子、分母同除以cos15°，有

=

=

=tan（15°－45°）

=tan（－30°）

=－.