高三理科数学教学质量检测(一)
数 学 试 题(理科)
本试卷分选择题和非选择题两部分,共4页. 满分150分. 考试时间120分钟.
注意事项:
1.答卷前,考生要务必填写答题卷上的有关项目.
2.选择题每小题选出答案后,用黑色字迹的钢笔或签字笔把答案代号填在答题卷对应的表格内.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.
4.考生必须保持答题卷的整洁.考试结束后,将答题卷和答题卡交回.
第一部分 选择题(共40分)
一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. ![]() ( ).
( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知![]() 为实数集,
为实数集,![]() ,则
,则![]() = ( ).
= ( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3. “![]() ” 是“函数
” 是“函数![]() 在区间
在区间![]() 上为增函数”的( ).
上为增函数”的( ).
A.充分条件不必要 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
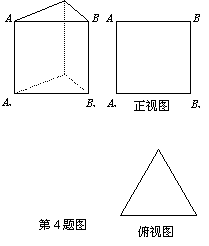
4.如图,矩形长为6,宽为4,在矩形内随机地撒300颗黄豆,数得落在椭圆外的黄豆数为96颗,以此实验数据为依据可以估计出椭圆的面积约为( ).
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 | |||
| |||
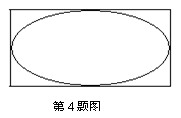
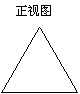
5.如图,水平放置的三棱柱的侧棱长和底边长均为2,
且侧棱![]() ,正视图是边长为2的正方形,
,正视图是边长为2的正方形,
该三棱柱的左视图面积为( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
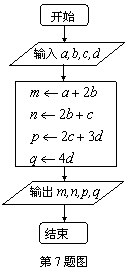 6.设
6.设![]() 为坐标原点,点M坐标为
为坐标原点,点M坐标为![]() ,若点
,若点![]() 满足不等式组:
满足不等式组: 则使
则使![]() 取得最大值的点
取得最大值的点![]() 的个数是( ) .
的个数是( ) .
A.![]() B.
B.![]() C.
C.![]() D.无数个
D.无数个
7.为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则如图所示,例如,明文![]() 对应密文
对应密文![]() . 当接收方收到密文
. 当接收方收到密文![]()
![]() 时,则解密得到的明文为( ).
时,则解密得到的明文为( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.定义运算![]() :
:![]() .设
.设![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的值域为( ).
的值域为( ).
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
第二部分 非选择题(共110分)
二、填空题(本大题共7小题,其中9—12题是必做题,13—15题是选做题.每小题5分,满分30分)
9.已知双曲线![]() ,则其渐近线方程为_________,离心率为________.
,则其渐近线方程为_________,离心率为________.
10.![]() 展开式中,常数项是__________.
展开式中,常数项是__________.
11. 设数列![]() 为公比
为公比![]() 的等比数列,若
的等比数列,若![]() 是方程
是方程![]() 的两根,则
的两根,则![]() _________.
_________.
12.已知函数![]() 的定义域是
的定义域是![]() (
(![]() 为整数),值域是
为整数),值域是![]() ,则满足条件的整数数对
,则满足条件的整数数对![]() 共有_________个.
共有_________个.
▲ 选做题:在下面三道小题中选做两题,三题都选只计算前两题的得分.
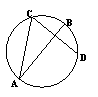 13. (几何证明选讲)如图,
13. (几何证明选讲)如图,![]() 、
、![]() 是圆
是圆![]() 的两条弦,且AB是线段CD的中垂线,已知AB=6,CD=
的两条弦,且AB是线段CD的中垂线,已知AB=6,CD=![]() ,则线段AC的长度为 .
,则线段AC的长度为 .
|
15.(不等式选讲)已知![]() ,则
,则![]() ,
,![]() 的取值范围为 .
的取值范围为 .
三、解答题(本大题共6题,共80分,解答应写出文字说明、证明过程或演算步骤)
 16.(本题满分12分)
16.(本题满分12分)
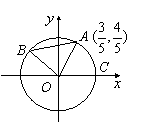
如图![]() 、
、![]() 是单位圆
是单位圆![]() 上的点,
上的点,![]() 是圆与
是圆与![]() 轴正半轴的交点,
轴正半轴的交点,![]() 点的坐标为
点的坐标为![]() ,三角形
,三角形![]() 为正三角形.
为正三角形.
(Ⅰ)求![]() ;
;
|
17.(本题满分12分)
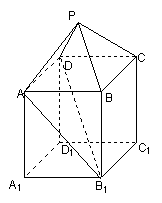
如图,在组合体中,![]() 是一个长方体,
是一个长方体,![]() 是一个四棱锥.
是一个四棱锥.![]() ,
,![]() ,点
,点![]() 且
且![]() .
.
(Ⅰ)证明:![]() ;
;
(Ⅱ)求![]() 与平面
与平面![]() 所成的角的正切值;
所成的角的正切值;
(Ⅲ)若![]() ,当
,当![]() 为何值时,
为何值时,![]() .
.
|
18.(本小题满分14分)
抛物线![]() 的准线的方程为
的准线的方程为![]() ,该抛物线上的每个点到准线
,该抛物线上的每个点到准线![]() 的距离都与到定点N的距离相等,圆N是以N为圆心,同时与直线
的距离都与到定点N的距离相等,圆N是以N为圆心,同时与直线![]() 相切的圆,
相切的圆,
(Ⅰ)求定点N的坐标;
(Ⅱ)是否存在一条直线![]() 同时满足下列条件:
同时满足下列条件:
① ![]() 分别与直线
分别与直线![]() 交于A、B两点,且AB中点为
交于A、B两点,且AB中点为![]() ;
;
② ![]() 被圆N截得的弦长为
被圆N截得的弦长为![]() .
.
19.(本小题满分14分)
佛山某公司生产陶瓷,根据历年的情况可知,生产陶瓷每天的固定成本为14000元,每生产一件产品,成本增加210元.已知该产品的日销售量![]() 与产量
与产量![]() 之间的关系式为
之间的关系式为
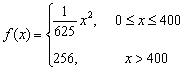 ,每件产品的售价
,每件产品的售价![]() 与产量
与产量![]() 之间的关系式为
之间的关系式为
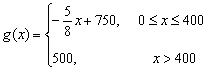 .
.
(Ⅰ)写出该陶瓷厂的日销售利润![]() 与产量
与产量![]() 之间的关系式;
之间的关系式;
(Ⅱ)若要使得日销售利润最大,每天该生产多少件产品,并求出最大利润.
20.(本小题满分14分)
设直线![]() . 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有
. 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有![]() . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”.
(Ⅰ)已知函数![]() .求证:
.求证:![]() 为曲线
为曲线![]() 的“上夹线”.
的“上夹线”.
(Ⅱ)观察下图:
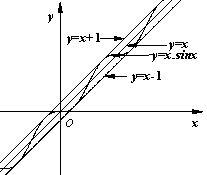
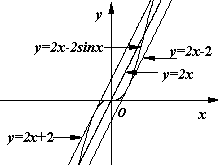
根据上图,试推测曲线![]() 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明.
21.(本小题满分14分)
数列![]() 满足
满足![]()
![]() .
.
(Ⅰ)求数列{![]() }的通项公式;
}的通项公式;
(Ⅱ)设数列{![]() }的前
}的前![]() 项和为
项和为![]() ,证明
,证明![]() .
.