1.6　三角函数模型简单应用

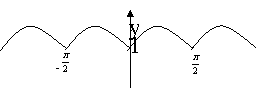1．你能利用函数的奇偶性画出图象吗？它与函数的图象有什么联系？

2．已知：，若(1)； (2)；

(3)α是第三象限角；(4)α∈R．分别求角α。

3．已知, 分别是方程的两个根，求角．

4．设A、B、C、D是圆内接四边形ABCD的四个内角，求证：

（1）sinA＝sinC；

（2）cos（A＋B）＝cos（C＋D）；

（3）tan（A＋B＋C）＝－tanD．

5．某商品一年内出厂价格在6元的基础上按月份随正弦曲线波动，已知3月份达到最高价格8元，7月份价格最低为4元，该商品在商店内的销售价格在8元基础上按月份随正弦曲线波动，5月份销售价格最高为10元，9月份销售价最低为6元，假设商店每月购进这种商品m件，且当月销完，你估计哪个月份盈利最大?

6．把一张纸卷到圆柱形的纸筒面上，卷上几圈．用剪刀斜着将纸筒剪断，再把卷着的纸展开，你就会看到：纸的边缘线是一条波浪形的曲线，试一试动手操作一下.它是正弦曲线吗？

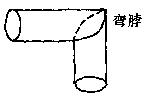
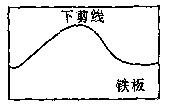7．如图，铁匠师傅在打制烟筒弯脖时，为确保对接成直角，在铁板上的下剪线正好是余弦曲线：的一个周期的图象，问弯脖的直径为12 时，应是多少?

8．已知函数f (x)=，试作出该函数的图象，并讨论它的奇偶性、周期性以及区间[0，]上的单调性。

9、（14分）如图，扇形AOB的半径为，扇形的圆心角为，PQRS是扇形的内接矩形，设∠AOP=θ，

（1） 试用θ表示矩形PQRS的面积y；

（2）利用正、余弦的和（差）与倍角公式化简矩形面积表达式y.

10.某人用绳拉车沿直线方向前进100米,若绳与行进方向的夹角为30°,人的拉力为20牛,则人对车所做的功为多少焦.

11．某港口水的深度y（米）是时间t，记作y=f(x),下面是某日水深的数

(时)	0	3	6	9	12	15	18	21	24
（米）	10	13	9.9	7	10	13	10	7	10

据：

经长期观察，y=f(t)的曲线可以近似地看成函数的图象。

12．已知△ABC的两边a, b ，它们的夹角为C　1°试写出△ABC面积的表达式；

2°当ÐC变化时，求△AABC面积的最大值。

13．已知定义在区间上的函数的图象关于直线对称，当时，函数，

其图象如图所示.

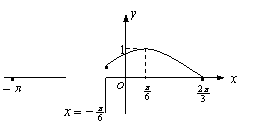求函数在的表达式；

14．绳子绕在半径为50cm的轮圈上，绳子的下端B处悬挂着物体W，如果轮子按逆时针方向每分钟匀速旋转4圈，那么需要多少秒钟才能把物体W的位置向上提升100cm?

15．如图，是正弦函数f(x)=Asin(ωx+φ)(A＞0,ω＞0)的一个周期的图像.

(1)写出f(x)的解析式；

(2)若g(x)与f(x)的图像关于直线x=2对称，写出g(x)的解析式.

（1）试根据以上数据，求出函数y=f(t)的近似表达式；

（2）一般情况下，船舶航行时，船底离海底的距离为5米或5米以上时认为是安全的（船舶停靠时，船底只需不碰海底即可），某船吃水深度（船底离水面的距离）为6.5米，如果该船希望在一天内安全进出港，请问，它至多能在港内停留多长时间？（忽略进出港所需的时间）

参考答案

1． 略

2．(1)(2)或(3)(4)或。

3．由已知得：得

∴k²-2k-3=0即k=3或k=-1.
又则，因此k=3舍去。
　　∴k=-1, 则, , ∴或

4．由已知A＋C＝，A＋B＋C＋D＝2得A＝－C，则sinA＝sin（－C）＝sinC，

又A＋B＝2－（C＋D），

故cos（A＋B）＝cos[2－（C＋D）]＝cos（C＋D）.

tan（A＋B＋C）＝tan（2－D）＝－tanD．

5．设出厂价波动函数为y₁＝6+Asin(ω₁x+φ₁)

易知A＝2　T₁＝8　ω₁＝　 +φ₁＝　φ₁＝-　∴y₁＝6+2sin(x-)

设销售价波动函数为y₂＝8+Bsin(ω₂x+φ₂)

易知B＝2　T₂＝8　ω₂＝　  +φ₂＝φ₂＝-

∴y₂＝8+2sin(x-)

每件盈利  y＝y₂-y₁＝［8+2sin(x-)］-［6+2sin(x-)］

＝2-2sinx

当sinx＝-1 x＝2kπ-x＝8k-2时y取最大值

当k＝1　即x＝6时　y最大　∴估计6月份盈利最大

6．略

7．弯脖的直径为12 cm，则周长为，周长正是函数的一个周期，即，得．

8．解：f (x)=sin2x

-1

f (-x)=sin(-2x)=sin2x=f (x)

∴f (x)为偶函数　　 T=

在[0,]上f (x)单调递增；在[,]上单调递减

9．解：（1）在直角三角形OPS中

SP=sinθ，OS=cosθ

矩形的宽SP=sinθ

因∠ROQ=

所以OR=RQ=SP=sinθ

矩形的长RS=OS－OR=cosθ－sinθ

所以面积：y=(cosθ－sinθ)sinθ　 (0﹤θ<)

10．

11．1）

2）由，即，解得

，在同一天内，取k=0，1得

∴该船希望在一天内安全进出港，可1时进港，17时离港，它至多能在港内停留16小时。

			x

B

12．解：

		a		c
	C　　D　　b　　 A

1°如图：设AC边上的高h=asinC

2°当C=90°时[sinC]_max=1　∴[S_△ABC]_max=

13．（1）当时，，当时

14．设需秒上升100cm .则（秒）

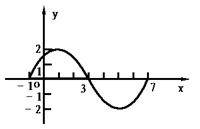
15． (1)f(x)=2sin(x+)　(2)g(x)=2sin(x-)