1.4　三角函数的图像与性质

一、选择题

1．若cosx=0，则角x等于(　)

A．kπ（k∈Z）　　　　　　　　　　　　　　　　　　　　　　　　B．+kπ（k∈Z）

C． +2kπ（k∈Z）　　　　　　　　　　　　　　　　　　　 D．－+2kπ（k∈Z）

2．使cosx=有意义的m的值为(　)

A．m≥0　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　B．m≤0

C．－1＜m＜1　　　　　　　　　　　　　　　　　　　　　　　　　D．m＜－1或m＞1

3．函数y=3cos（x－）的最小正周期是(  )

A．　　　　　　　　　　　　 B．　　　　　　　　　　　 C．2π　　　　　　　　　　　　　D．5π

4．函数y=（x∈R）的最大值是(　)

A．　　　　　　　　　　　　　 B．　　　　　　　　　　　　　　　　 C．3　　　　　　　　　　　　　　　　　 D．5

5．函数y=2sin²x+2cosx－3的最大值是(　)

A．－1　　　　　　　　　　　　　B．　　　　　　　　　　　　　　　　 C．－　　　　　　　　　　　D．－5

6．函数y=tan的最小正周期是(  )

A．aπ　　　　　　　　　　　　　　B．aπ　　　　　　　　　　　　 C．　　　　　　　　　　　　 D．

7．函数y=tan（－x）的定义域是(　)

A．{xx≠，x∈R}　　　　　　　　　　　　　　　　　　　　　B．{xx≠－，x∈R}

C．{xx≠kπ+，k∈Z，x∈R}　　　　　　　　　　　　　D．{xx≠kπ+，k∈Z，x∈R}

8．函数y=tanx（－≤x≤且x≠0）的值域是(　)

A．［－1，1］　　　　　　　　　　　　　　　　　　　　　　　　　B．［－1，0）∪（0，1］

C．（－∞，1］　　　　　　　　　　　　　　　　　　　　　 D．［－1，+∞）

9．下列函数中，同时满足①在（0，）上是增函数，②为奇函数，③以π为最小正周期的函数是(　)

A．y=tanx　　　　　　　　　　　B．y=cosx　　　　　　　　　　　　　 C．y=tan　　　　　　　　　D．y=sinx

10．函数y=2tan（3x－）的一个对称中心是(  )

A．（，0）　　　　　　　 B．（，0）　　　　　　　 C．（－，0）　　　　　 D．（－，0）

二、解答题

11．比较下列各数大小：

（1）tan2与tan9；

（2）tan1与cot4．

12．已知α、β∈（，π），且tanα＜cotβ，求证：α+β＜．

13．求函数y=tan²x+tanx+1（x∈R且x≠+kπ，k∈Z）的值域．

14．求函数y=－2tan（3x+）的定义域、值域，并指出它的周期、奇偶性和单调性．

15求函数y=+lg（36－x²）的定义域．

参考答案

一、选择题

1．B  2． B　　3．D  4． C　 5． C　 6．B　 7． D　 8．B　 9．A　 10． C

二、解答题

11．分析：同名函数比较大小时，应化为同一单调区间上两个角的函数值后，应用函数的单调性解决；而对于不同名函数，则应先化为同名函数再按上面方法求解．

解：（1）tan9=tan（－2π+9），

因为<2<－2π+9<π，

而y=tanx在（，π）内是增函数，

所以tan2<tan（－2π+9），

即tan2<tan9．

（2）cot4=tan（－4）=tan（－4），

0<－4<1<，

而y=tanx在（0，）内是增函数，

所以tan（－4）<tan1，

即cot4<tan1．

点评：比较两个三角函数值的大小，应先将函数名称统一，再利用诱导公式将角转化到同一个单调区间内，通过函数的单调性处理．

12．证明：∵tanα<cotβ，

∴tanα<tan（－β）．

又∵<α<π，<－β<π，

∴α与－β落在同一单调区间．

∴α<－β，即α+β<．

13．解：设t=tanx，由正切函数的值域可得t∈R，

则y=t²+t+1=（t+）²+≥．

∴原函数的值域是［，+∞）．

点评：由于正切函数的值域为R，所以才能在R上求二次函数的值域．

14．解：由3x+≠kπ+，得x≠（k∈Z），

∴所求的函数定义域为{xx≠（k∈Z）}，值域为R，周期为，

它既不是奇函数，也不是偶函数．

kπ－≤3x+≤kπ+（k∈Z），

∴≤x≤（k∈Z）．

在区间［，］（k∈Z）上是单调减函数．

15．解：欲求函数定义域，则由

即

也即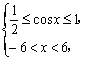

解得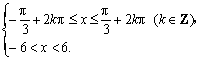

取k=－1、0、1，可分别得到

x∈（－6，－）或x∈［－，］或x∈［，6），

即所求的定义域为（－6，－）∪［－，］∪［，6）