1.3 三角函数的诱导公式
一、选择题:
1.已知sin(![]() +α)=
+α)=![]() ,则sin(
,则sin(![]() -α)值为( )
-α)值为( )
A.
![]() B. —
B. —![]() C.
C. ![]() D. —
D. —![]()
2.cos(![]() +α)= —
+α)= —![]() ,
,![]() <α<
<α<![]() ,sin(
,sin(![]() -α) 值为( )
-α) 值为( )
A.
![]() B.
B. ![]() C.
C. ![]() D. —
D. —![]()
3.化简:![]() 得(
)
得(
)
A.sin2+cos2 B.cos2-sin2 C.sin2-cos2 D.± (cos2-sin2)
4.已知α和β的终边关于x轴对称,则下列各式中正确的是( )
A.sinα=sinβ B. sin(α-![]() ) =sinβ
) =sinβ
C.cosα=cosβ D. cos(![]() -α) =-cosβ
-α) =-cosβ
5.设tanθ=-2, ![]() <θ<
<θ<![]() ,那么sin
,那么sin![]() θ+cos(θ-
θ+cos(θ-![]() )的值等于(
),
)的值等于(
),
A.
![]() (4+
(4+![]() )
B.
)
B. ![]() (4-
(4-![]() )
C.
)
C. ![]() (4±
(4±![]() ) D.
) D. ![]() (
(![]() -4)
-4)
二、填空题:
6.sin(-![]() )= .
)= .
7.cos(![]() -x)=
-x)= ![]() ,x∈(-
,x∈(-![]() ,
,![]() ),则x的值为 .
),则x的值为 .
8.tanα=m,则![]() .
.
9.sinα=sin(-![]() +α),则α的取值范围是 .
+α),则α的取值范围是 .
10.若α为锐角,则2logsecαcos(![]() -α)=
.
-α)=
.
三、解答题:
11.![]() .
.
12.已知:sin(x+![]() )=
)=![]() ,求sin(
,求sin(![]() +cos2(
+cos2(![]() -x)的值.
-x)的值.
13. 求下列三角函数值:
(1)sin![]() ;(2)cos
;(2)cos![]() ;(3)tan(-
;(3)tan(-![]() );(4)sin(-765°).
);(4)sin(-765°).
14. 求下列三角函数值:
(1)sin![]() ·cos
·cos![]() ·tan
·tan![]() ;
;
(2)sin[(2n+1)π-![]() ].
].
15.设f(θ)=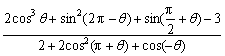 ,求f(
,求f(![]() )的值.
)的值.
参考答案
一、选择题:
1.C 2.A 3.C 4.C 5.A
二、填空题:
6.![]() 7.±
7.±![]() 8.
8.![]() 9.[(2k-1)
9.[(2k-1) ![]() ,2k
,2k![]() ] 10.2
] 10.2
三、解答题:
11.原式=![]() =
=![]() = sinα
= sinα
12.![]()
13.解:(1)sin![]() =sin(2π+
=sin(2π+![]() )=sin
)=sin![]() =
=![]() .
.
(2)cos![]() =cos(4π+
=cos(4π+![]() )=cos
)=cos![]() =
=![]() .
.
(3)tan(-![]() )=cos(-4π+
)=cos(-4π+![]() )=cos
)=cos![]() =
=![]() .
.
(4)sin(-765°)=sin[360°×(-2)-45°]=sin(-45°)=-sin45°=-![]() .
.
注:利用公式(1)、公式(2)可以将任意角的三角函数转化为终边在第一象限和第二象限的角的三角函数,从而求值.
14.解:(1)sin![]() ·cos
·cos![]() ·tan
·tan![]() =sin(π+
=sin(π+![]() )·cos(4π+
)·cos(4π+![]() )·tan(π+
)·tan(π+![]() )
)
=(-sin![]() )·cos
)·cos![]() ·tan
·tan![]() =(-
=(-![]() )·
)·![]() ·1=-
·1=-![]() .
.
(2)sin[(2n+1)π-![]() ]=sin(π-
]=sin(π-![]() )=sin
)=sin![]() =
=![]() .
.
15.解:f(θ)=![]()
=![]()
=![]()
=![]()
=![]()
=![]()
=cosθ-1,
∴f(![]() )=cos
)=cos![]() -1=
-1=![]() -1=-
-1=-![]() .
.
