高三年级数学(文科)第一次调研考试
数学(文科) 2008.3
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个备选项中,有且只有一项是符合题目要求的.
1.
设集合![]() ,则满足条件
,则满足条件![]() 的集合
的集合![]() 的个数是 ( )
的个数是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.
已知命题“若![]() 则
则![]() ”为真,则下列命题中一定为真的是 ( )
”为真,则下列命题中一定为真的是 ( )
A.若![]() 则
则![]() B.若
B.若![]() 则
则![]()
C.若![]() 则
则![]() D.若
D.若![]() 则
则![]()
3.
若![]() ,则点
,则点![]() 位于 ( )
位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.
在等差数列![]() 中,已知
中,已知![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,则
项和,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.
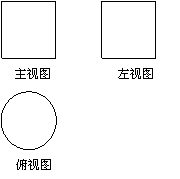 如图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的全面积为 ( )
如图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的全面积为 ( )
A.![]()
B.![]()
C.![]()
D.![]()
6.
函数![]() 的零点个数是 ( )
的零点个数是 ( )
A.![]() 个 B.
个 B.![]() 个 C.
个 C.![]() 个 D.
个 D.![]() 个
个
7.
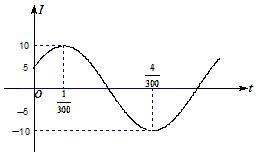 电流强度
电流强度![]() (安)随时间
(安)随时间![]() (秒)变化的函数
(秒)变化的函数![]() (
(![]() ,
,![]() )的图像如图所示,则当
)的图像如图所示,则当![]() 时,电流强度是 ( )
时,电流强度是 ( )
A.![]() 安
安
B.![]() 安
安
C.![]() 安
安
D.![]() 安
安
8.
若函数![]() 在
在![]() 上是增函数,则实数
上是增函数,则实数![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.
甲、乙两人各抛掷一次正方体骰子(它们的六个面分别标有数字![]() ),设甲、乙所抛掷骰子朝上的面的点数分别为
),设甲、乙所抛掷骰子朝上的面的点数分别为![]() 、
、![]() ,则满足复数
,则满足复数![]() 的实部大于虚部的概率是 [www.shulihua.net] ( )
的实部大于虚部的概率是 [www.shulihua.net] ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.
在![]() 平面上,横坐标与纵坐标均为整数的点称为整点.对任意
平面上,横坐标与纵坐标均为整数的点称为整点.对任意![]() ,连接原点
,连接原点![]() 与点
与点![]() ,用
,用![]() 表示线段
表示线段![]() 上除端点外的整点个数,则
上除端点外的整点个数,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:本大题共5小题,每小题5分,共20分.其中第13题前一空2分,后一空3分;第14、15两小题是选做题,考生只能选做一题,若两题都做,则只以第14题的得分为最后得分.
11.
已知![]() ,
,![]() ,以
,以![]() 与
与![]() 同向,则
同向,则![]() .
.
12.
准线方程为![]() 的抛物线的标准方程是 .
的抛物线的标准方程是 .
13.
图(1)、(2)、(3)、(4)分别包含1个、5个、13个、25个第二十九届北京奥运会吉祥物“福娃迎迎”,按同样的方式构造图形,设第![]() 个图形包含
个图形包含![]() 个“福娃迎迎”,则
个“福娃迎迎”,则![]() ;
;![]() .(答案用数字或
.(答案用数字或![]() 的解析式表示)
的解析式表示)

14.
(坐标系与参数方程选做题)在极坐标系中,直线![]() (
(![]() )与圆
)与圆![]()
![]() 交于
交于![]() 、
、![]() 两点,则
两点,则![]() .
.
15.
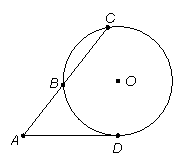
如图,从圆![]() 外一点
外一点![]() 引圆的切线
引圆的切线![]() 和割线
和割线![]() ,已知
,已知![]() ,
,![]() ,圆
,圆![]() 的半径为
的半径为![]() ,则圆心
,则圆心![]() 到
到![]() 的距离为 .
的距离为 .
三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.
16. (本小题满分12分)
在![]() 中,已知
中,已知![]() ,
,![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若![]() 的面积
的面积![]() ,求
,求![]() 的值.[www.shulihua.net]
的值.[www.shulihua.net]
17. (本小题满分12分)
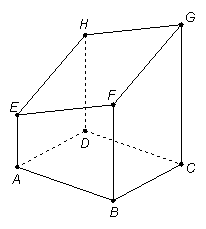
如图是以正方形![]() 为底面的正四棱柱被一平面所截得的几何体,四边形
为底面的正四棱柱被一平面所截得的几何体,四边形![]() 为
为
截面,且![]() ,
,![]() .
.
(Ⅰ)证明:截面四边形![]() 是菱形;
是菱形;
(Ⅱ)求三棱锥![]() 的体积.
的体积.
18. (本小题满分14分)
某旅游商品生产企业,2007年某商品生产的投入成本为1元/件,出厂价为流程图的输
出结果![]() 元/件,年销售量为10000件,因2008年国家长假的调整,此企业为适应市场需求,计划提高产品档次,适度增加投入成本.若每件投入成本增加的比例为
元/件,年销售量为10000件,因2008年国家长假的调整,此企业为适应市场需求,计划提高产品档次,适度增加投入成本.若每件投入成本增加的比例为![]() (
(![]() ),则出厂价相应提高的比例为
),则出厂价相应提高的比例为![]() ,同时预计销售量增加的比例为
,同时预计销售量增加的比例为![]() .已知得利润
.已知得利润![]() (出厂价
(出厂价![]() 投入成本)
投入成本)![]() 年销售量.
年销售量.
(Ⅰ)写出2008年预计的年利润![]() 与投入成本增加的比例
与投入成本增加的比例![]() 的关系式;
的关系式;
(Ⅱ)为使2008年的年利润比2007年有所增加,问:投入成本增加的比例![]() 应在什么范围内?
应在什么范围内?
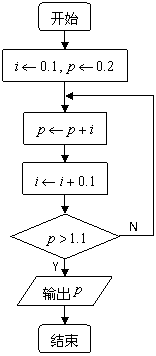 |
19. (本小题满分14分)
已知椭圆![]() 的焦点在
的焦点在![]() 轴上,长轴长为
轴上,长轴长为![]() ,离心率为
,离心率为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)已知点![]() 和直线
和直线![]() :
:![]() ,线段
,线段![]() 是椭圆
是椭圆![]() 的一条弦且直线
的一条弦且直线![]() 垂直平
垂直平
分弦![]() ,求实数
,求实数![]() 的值.
的值.
20. (本小题满分14分)
设数列![]() 的前
的前![]() 项和为
项和为![]() ,其中
,其中![]() ,
,![]() 为常数,且
为常数,且![]() 、
、![]() 、
、![]() 成等差数列.
成等差数列.
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,问:是否存在
,问:是否存在![]() ,使数列
,使数列![]() 为等比数列?若存在,求出
为等比数列?若存在,求出![]() 的值;
的值;
若不存在,请说明理由.[www.shulihua.net]
21. (本小题满分14分)
已知抛物线![]() 与直线
与直线![]() 相切于点
相切于点![]() .
.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
数学(文科)参考答案
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个备选项中,有且只有一项是符合题目要求的.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | B | D | C | A | A | B | A | B | C |
二、填空题:本大题共5小题,每小题5分,共20分.其中第13题前一空2分,后一空3分;第14、15两小题是选做题,考生只能选做一题,若两题都做,则只以第14题的得分为最后得分.
11.![]() 12.
12.![]() 13.
13.![]() ,
,![]()
14.![]() 15.
15.![]()
三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.
16.
解:(Ⅰ)由![]() 得
得![]() ,由此及
,由此及
![]() ,即
,即![]()
得![]() ,故
,故![]() ;
;
(Ⅱ)由![]() 得
得![]() ,由此及余弦定理得
,由此及余弦定理得
![]() ,
,
故![]() .
.
17.
解:(Ⅰ)证明:因为平面![]() ∥平面
∥平面![]() ,且平面
,且平面![]() 分别交平面
分别交平面![]() 、
、
平面![]() 于直线
于直线![]() 、
、![]() ,所以
,所以![]() ∥
∥![]() .
.
同理,![]() ∥
∥![]() .
.
因此,四边形![]() 为平行四边形. ……(1)
为平行四边形. ……(1)
因为![]() ,而
,而![]() 为
为![]() 在底面
在底面![]() 上的射影,所以
上的射影,所以![]() .
.
因为![]() ,所以
,所以![]() ∥
∥![]() .
.
因此,![]() . ……(2)
. ……(2)
由(1)、(2)可知:四边形![]() 是菱形;
是菱形;
(Ⅱ)因为![]() 平面
平面![]() ,
,![]() ∥
∥![]() ,所以
,所以![]() 到平面
到平面![]() 的距离为
的距离为![]() .于是,由等体积法得所求体积
.于是,由等体积法得所求体积
![]() .
.
18.
解:(Ⅰ)由流程图可知:![]() .依题意,得
.依题意,得
![]()
![]() (
(![]() );
);
(Ⅱ)要保证2008年的利润比2007年有所增加,当且仅当
![]() ,即
,即![]() .
.
解之得![]() .
.
19.
解:(Ⅰ)![]() ;
;
(Ⅱ)由条件可得直线![]() 的方程为
的方程为![]() .于是,有
.于是,有
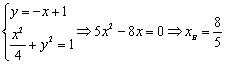 ,
,![]() .
.
设弦![]() 的中点为
的中点为![]() ,则由中点坐标公式得
,则由中点坐标公式得![]() ,
,![]() ,由此及点
,由此及点![]() 在直线
在直线![]() 得
得
![]() .
.
20.
解:(Ⅰ)依题意,得![]() .于是,当
.于是,当![]() 时,有[www.shulihua.net]
时,有[www.shulihua.net] ![]() .
.
两式相减,得![]() (
(![]() ).
).
又因为![]() ,
,![]() ,所以数列
,所以数列![]() 是首项为
是首项为![]() 、公比为3的等比数列.
、公比为3的等比数列.
因此,![]() (
(![]() );
);
(Ⅱ)因为![]() ,所以
,所以
![]() .
.
要使![]() 为等比数列,当且仅当
为等比数列,当且仅当![]() ,即
,即![]() .
.
21. 解:(Ⅰ)依题意,有
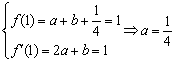 ,
,![]() .
.
因此,![]() 的解析式为
的解析式为![]() ;[www.shulihua.net]
;[www.shulihua.net]
(Ⅱ)由![]() (
(![]() )得
)得![]() (
(![]() ),解之得
),解之得
![]() (
(![]() )
)
由此可得
![]() 且
且![]() ,
,
所以实数![]() 的取值范围是
的取值范围是![]() .
.
