高三年级理科数学第三次月考
理科数学试卷
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设全集![]() ,集合M={1,3,5},
,集合M={1,3,5},![]() ,则集合
,则集合![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.在等差数列![]() 中,
中,![]() ,则
,则![]()
A.24 B.![]()
3.已知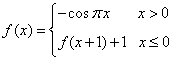 ,则
,则![]() 的值等于
的值等于
A.![]() B.
B.
4.已知定义在![]() 上的奇函数
上的奇函数![]() 满足
满足![]() ,则
,则![]() 的值为
的值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
|
|
| 0 |
|
| 0.592 | 1 |
5.若指数函数![]() 的部分对应值如右表:
的部分对应值如右表:
则不等式![]() 的解集为
的解集为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.设常数![]() ,
,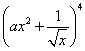 展开式中
展开式中![]() 的系数为
的系数为![]() ,则
,则![]()
A.![]()
![]() B.
B.![]() C.1
D.2
C.1
D.2
7.已知![]() ,把数列
,把数列![]() 的各项排列成如下的三角形状:
的各项排列成如下的三角形状: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
……………………………………
记![]() 表示第
表示第![]() 行的第
行的第![]() 个数,则A(21,12)=
个数,则A(21,12)=
A.411 ![]() B.
B.
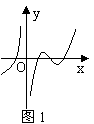
8.设函数![]() ,则
,则![]()
A.在区间![]() 上是增函数 B.在区间
上是增函数 B.在区间![]() 上是减函数
上是减函数
 C.在区间
C.在区间![]() 上是增函数
D.在区间
上是增函数
D.在区间![]() 上是减函数
上是减函数
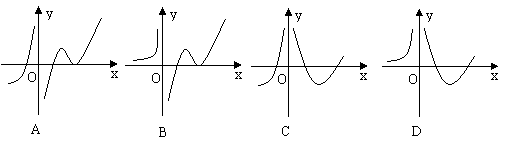
9.设函数f(x)在定义域内可导,y=f(x)的图象如图1所示,
则导函数y=f ¢(x)可能为
 |
10.将5名实习教师分配到高一年级的3个班实习,每班至少1名,最多2名,则不同的分配方案有
(A)30种 (B)90种
(C)180种 (D)270种
二、填空题:本大题共6小题,每小题4分,共24分,把答案填写在题中的横线上。
11.函数![]() 的定义域是_______________
的定义域是_______________
12.已知![]() 、
、![]() 均为锐角,且
均为锐角,且![]() ,则
,则![]() ________
________
13.设数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,则
,则![]() _____
_____
14.将函数![]() 的图象上每一点的纵坐标不变,横坐标变为原来的
的图象上每一点的纵坐标不变,横坐标变为原来的![]() 倍,得到图象C,若将
倍,得到图象C,若将![]() 的图象向上平移2个单位,也得到图象C,则
的图象向上平移2个单位,也得到图象C,则![]() _______
_______
15.设![]() ,
,![]() ,计算
,计算![]() ________,
________,![]() ________,并由此概括出关于函数
________,并由此概括出关于函数![]() 和
和![]() 的一个等式,使上面的两个等式是你写出的等式的特例,这个等式是_______________
的一个等式,使上面的两个等式是你写出的等式的特例,这个等式是_______________
16. 计算:![]() ___________
___________
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二、填空题:
11. ; 12. ; 13. ;14.
15._____;_____;_______________________________; 16.____________
三、解答题:本大题共6个小题,共76分。解答应写出文字说明、证明过程或演算步骤。
17.某地区为下岗人员免费提供财会和计算机培训,以提高下岗人员的再就业能力,每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有60%,参加过计算机培训的有75%,假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.
(I)任选1名下岗人员,求该人参加过培训的概率;
(II)任选3名下岗人员,记![]() 为3人中参加过培训的人数,求
为3人中参加过培训的人数,求![]() 的分布列和期望.
的分布列和期望.
18.将函数![]() 在区间
在区间![]() 内的全部极值点按从小到大的顺序排成数列
内的全部极值点按从小到大的顺序排成数列![]() ,
,![]() .
.
(Ⅰ)求数列![]() 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设![]() ,求证:
,求证:![]() ,
,![]() .
.
19.如图,
在直三棱柱ABC-A1B![]()
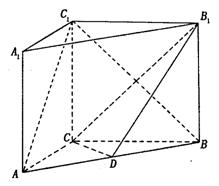 AA1=4,点D是AB的中点,
AA1=4,点D是AB的中点,
(1)求证:AC⊥BC1;
(2)求证:AC 1//平面CDB1;
(3)求二面角B-CD-B1 大小;
20.已知函数![]() 。
。
(Ⅰ)若函数![]() 的图象关于点
的图象关于点![]() 对称,且
对称,且![]() ,求
,求![]() 的值;
的值;
(Ⅱ)设![]() ,若
,若![]() 是
是![]() 的充分条件,求实数
的充分条件,求实数![]() 的取值范围。
的取值范围。
21.已知![]() 在区间
在区间![]() 上是增函数。
上是增函数。
(Ⅰ)求实数![]() 的值所组成的集合
的值所组成的集合![]() ;
;
(Ⅱ)设关于![]() 的方程
的方程![]() 的两个根为
的两个根为![]() 、
、![]() ,若对任意
,若对任意![]() 及
及![]() ,不等式
,不等式
![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
22.已知首项不为零的数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意的
,若对任意的![]() 、
、![]() ,都有
,都有![]() .
.
(Ⅰ)判断![]() 是否为等差数列,并证明你的结论;
是否为等差数列,并证明你的结论;
(Ⅱ)若![]() ,数列
,数列![]() 的第
的第![]() 项
项![]() 是数列
是数列![]() 的第
的第![]() 项
项![]() ,求
,求![]() .
.
(Ⅲ)求和![]() .
.
参考答案
一、选择题:AADBD CBADB
二、填空题:
11. ![]() 12. 1
13. 9
14.
12. 1
13. 9
14. ![]()
15. 0,0 ,![]() 16.
16. ![]()
三、解答题
17. 解:任选1名下岗人员,记“该人参加过财会培训”为事件![]() ,“该人参加过计算机培训”为事件
,“该人参加过计算机培训”为事件![]() ,由题设知,事件
,由题设知,事件![]() 与
与![]() 相互独立,且
相互独立,且![]() ,
,![]() .
.
(I)解法一:任选1名下岗人员,该人没有参加过培训的概率是
![]()
所以该人参加过培训的概率是![]() .
.
解法二:任选1名下岗人员,该人只参加过一项培训的概率是
![]()
该人参加过两项培训的概率是![]() .
.
所以该人参加过培训的概率是![]() .
.
(II)因为每个人的选择是相互独立的,所以3人中参加过培训的人数![]() 服从二项分布
服从二项分布![]() ,
,![]() ,
,![]() ,即
,即![]() 的分布列是
的分布列是
|
| 0 | 1 | 2 | 3 |
|
| 0.001 | 0.027 | 0. 243 | 0.729 |
![]() 的期望是
的期望是![]() .
.
(或![]() 的期望是
的期望是![]() )
)
18. 解:(Ⅰ)∵![]()
![]()
∴![]() 的极值点为
的极值点为![]() ,从而它在区间
,从而它在区间![]() 内的全部极值点按从小到大排列构成以
内的全部极值点按从小到大排列构成以![]() 为首项,
为首项,![]() 为公差的等差数列,∴
为公差的等差数列,∴![]() ,
,![]()
(Ⅱ)由![]() 知对任意正整数
知对任意正整数![]() ,
,![]() 都不是
都不是![]() 的整数倍,
的整数倍,
所以![]() ,从而
,从而![]()
于是![]()
又![]() ,
,
![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列。 ∴
为公比的等比数列。 ∴![]() ,
,![]()
19. (1)直三棱柱ABC-A1B
∴ AC⊥BC,又 AC⊥![]() C,∴ AC⊥平面BCC1;∴ AC⊥BC1
C,∴ AC⊥平面BCC1;∴ AC⊥BC1
(2)设CB1与C1B的交点为E,连结DE,∵ D是AB的中点,E是BC1的中点,∴ DE//AC1,
∵ DE![]() 平面CDB1,AC1
平面CDB1,AC1![]() 平面CDB1,∴ AC1//平面CDB1;
平面CDB1,∴ AC1//平面CDB1;
(3)作BE ![]() CD交CD延长线于F ,则
CD交CD延长线于F ,则![]() 为所求的二面角。
为所求的二面角。
![]() 故可求
故可求![]() ,求出
,求出![]() =
=![]()
20. 解:(Ⅰ)∵ ![]()
![]()
∴
![]() ,
,
∴![]() 的图象的对称中心为
的图象的对称中心为![]()
又已知点![]() 为
为![]() 的图象的一个对称中心,∴
的图象的一个对称中心,∴![]()
而![]() ,∴
,∴![]() 或
或![]() 。
。
(Ⅱ)若![]() 成立,即
成立,即![]() 时,
时,![]() ,
,![]() ,
,
由![]() ,
,
∵ ![]() 是
是![]() 的充分条件,∴
的充分条件,∴![]() ,解得
,解得![]() ,即
,即![]() 的取值范围是
的取值范围是![]() 。
。
21. 解:(Ⅰ) ![]() ,
,
∵![]() 在区间
在区间![]() 上是增函数,∴
上是增函数,∴![]() 对
对![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立
恒成立
设![]() ,则问题等价于
,则问题等价于 ![]() , ∴
, ∴ ![]()
(Ⅱ)由![]() ,得
,得![]() ,
,
∵![]() ∴
∴![]() 是方程
是方程![]() 的两非零实根,
的两非零实根,
∴![]() ,从而
,从而![]() ,
,
∵![]() ,∴
,∴![]() .
.
∴不等式![]() 对任意
对任意![]() 及
及![]() 恒成立
恒成立
![]() 对任意
对任意![]() 恒成立
恒成立![]() 对任意
对任意![]() 恒成立
恒成立
设![]() ,则问题又等价于
,则问题又等价于
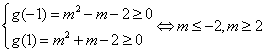 即
即 ![]() 的取值范围是
的取值范围是![]() .
.
22. 解:(Ⅰ)![]() 是等差数列,证明如下:
是等差数列,证明如下:
∵![]() ,令
,令![]() ,由
,由![]() 得
得![]() 即
即![]() .
.
∴![]() 时,
时,![]() ,且
,且![]() 时此式也成立.
时此式也成立.
∴![]() ,即
,即![]() 是以
是以![]() 为首项,2
为首项,2![]() 为公差的等差数列.
为公差的等差数列.
(Ⅱ)![]() 时,由(Ⅰ)知
时,由(Ⅰ)知![]() ,
,
依题意,![]() 时,
时,![]() ,∴
,∴![]() ,又
,又![]() ,
,
∴![]() 是以2为首项,2为公比的等比数列,
是以2为首项,2为公比的等比数列,![]() 即
即![]() .
.
(Ⅲ)∵ ![]()
∴ ![]()
即 ![]()
![]()
两式相减,可以求得![]()