高三数学四校联考模拟最新试题
数学试题
考生注意：
本卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分。考试时间150分钟。考试结束后将第Ⅱ卷和答题卡一并交回。
第Ⅰ卷（选择题，共60分）
注意事项：
1．答第I卷前，考生务必将自己的姓名、准考证号、考试科目、试卷类型用2B铅笔涂写在答题卡上。
2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其它答案标号。不能答在试卷上。
一、选择题：本大题共12小题；每小题5分，共计60分。在每小题列出的四个选项只有一项是最符合题目要求的。
1．复数
的虚部是 （ ）
|
2．已知集合
，R是实数集，则（ B）∩A=
（ ）
A．[0，1] B．
C．
D．以上都不对
3．甲、乙、丙、丁四位同学各自对A、B两变量的线性相关性作试验，并用回归分析方法分
别求得相关系数r与残差平方和m如下表： （ ）
| 甲 | 乙 | 丙 | 丁 | |
| r | 0.82 | 0.78 | 0.69 | 0.85 |
| m | 106 | 115 | 124 | 103 |
则哪位同学的试验结果体现A、B两变量有更强的线性相关性？
A．甲 B．乙 C．丙 D．丁
4．已知条件p:x≤1，条件，q：
<1，则
p是q的 （ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．即非充分也非必要条件
5．若函数f(x)=sinax+cosax(a>0)的最小正周期为1，则它的图像的一个对称中心为 （ ）
| |
，0） B．（0，0） C．（－
，0） D．（，0）
6．若
的展开式各项系数和为64，则展开式中的常数项为 （ ）
A．－540 B．－162 C．162 D．540
7．曲线
与坐标轴所围成的图形的面积是 （ ）
A．2 B．3 C．
D．4
|
A．
≥9 B．≥10
C．≤10 D．≤9
9．已知函数f(x)=2x的反函数f－1(x)满足
f－1(a)+
f－1(b)=4，则
的最小值为（ ）
A．1 B．
C．
D．
10．过抛物线y2=4x的焦点作一条直线与抛物线相交
于A、B两点，它们的横坐标之和等于5，则这样
的直线 （ ）
A．有且仅有一条 B．有且仅有两条
C．有无穷多条 D．不存在
11．设偶函数f(x)=logaax+b在（0，+∞）上单调递增，则f(b－2)与f(a+1)的大小关系是（ ）
A．f(b－2)=f(a+1) B．f(b－2)>f(a+1) C．f(b－2)<f(a+1) D．不能确定
|
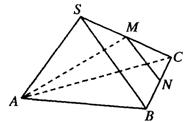
顶点在底面上的射影是底面的中心的棱锥为正棱锥）
M、N分别是棱SC，BC的中点，且MN⊥AM，若
侧棱SA=2
，则此正三棱锥S—ABC外接球的
表面积是（ ）
A．45π B．32π C．12π D．36π
第Ⅱ卷（非选择题 共90分）
注意事项：
1．第Ⅱ卷用钢笔或圆珠笔直接答在试题卷中（除题目有特殊规定外）。
2．答卷前将密封线内项目填写清楚。
二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上.
13．已知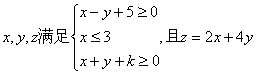
的最小值为－6，则常数k=
.
14．观察下式：1=12，2+3+4=32，3+4+5+6+7=52，4+5+6+7+8+9+10=72，…，则可得出一般结论： .
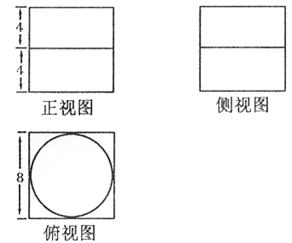
15．下图是一个物体的三视图，根据图中尺寸（单位：cm），它的体积为 cm3.
|
16．已知两个点M（－5，0）和N（5，0），若直线上存在点P，使PM－PN=6，则称该直线为“B型直线”，给出下列直线：①y=x+1，②y=
x, ③y=2，④y=2x+1，其中为“B型直线”的是 .（填上所有正确结论的序号）
三、解答题：本大题共6小题，共计74分.解答应写出文字说明、证明过程或推演步骤.
17．（本小题满分12分）
在△ABC中，角A、B、C的对边分别为a、b、c，且满足（2a－c）cosB=bcosC.
（Ⅰ）求角B的大小；
| |
的最大值是5，求k的值.
18．（本小题满分12分）
|
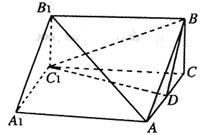
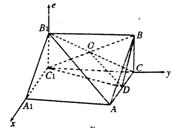
（Ⅰ）求证：AB1//面BDC1；
（Ⅱ）求二面角C1—BD—C的余弦值；
（Ⅲ）在侧棱AA1上是否存在点P，使得
CP⊥面BDC1？并证明你的结论.
19．（本小题满分12分）
有A，B，C，D四个城市，它们都有一个著名的旅游点，依此记为a，b，c，d.把ABCD和a，b，c，d分别写成左、右两列，现在一名旅游爱好者随机用4条线把左右两边的字母全部连接起来，构成“一一对应”，已知每连对一个得2分，连错得0分；
（Ⅰ）求该爱好者得分的分布列；
（Ⅱ）求该爱好者得分的数期望.
20．（本小题满分12分）
已知定义在R上的单调函数y=f(x)，当x<0时，f(x)>1，且对任意的实数x、y∈R，有f(x+y)=f(x)f(y)，
（Ⅰ）求f(0)，并写出适合条件的函数f(x)的一个解析式；
（Ⅱ）数列{an}满足
,
①求通项公式an的表达式；
②令
，
试比较Sn与Tn的大小，并加以证明.
21．（本小题满分12分）
已知动圆P与定圆B：
内切，且动圆P经过一定点A（
，
0），
（Ⅰ）求动圆圆心P的轨迹方程；
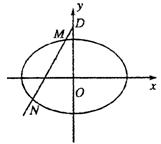
（Ⅱ）若已知点D（0，3），M、N在动点P的轨迹上，且
，求实数
的取
值范围.
22．（本小题满分12分）
已知函数f(x)=ax3+bx2－3x在x=±1处取得极值.
（Ⅰ）求函数f(x)的解析式；
（Ⅱ）求证：对于区间[－1，1]上任意两个自变量的值x1，x2，都有f(x1)－f(x2)≤4；
（Ⅲ）若过点A（1，m）（m≠－2）可作曲线y=f(x)的三条切线，求实数m的取值范围.
参考答案
一、选择题（每小题5分，共12小题）
BADAC ABBCB CD
二、填空题（每小题4分，共4小题）
13．0
14．n+(n+1)+…+(3n－2)=(2n－1)2
15．256+64π
16．①③
三、解答题
（I）∵(2a－c)cosB=bcosC，
∴（2sinA－sinC）cosB=sinBcosC.……………………………………………2分
即2sinAcosB=sinBcosC+sinCcosB
=sin(B+C)
∵A+B+C=π，∴2sinAcosB=sinA.…………………………………………4分
∵0<A<π,∴sinA≠0.
∴cosB=.…………………………………………………………………5分
∵0<B<π，∴B=
.…………………………………………………………6分
（II）
=4ksinA+cos2A.…………………………………………………………7分
=－2sin2A+4ksinA+1，A∈（0，
）……………………………………9分
设sinA=t，则t∈
.
则=－2t2+4kt+1=－2(t－k)2+1+2k2,t∈.…………………………10分
∵k>1，∴t=1时，取最大值.
依题意得，－2+4k+1=5，∴k=
.………………………………………………12分
（18）（I）证明：
连接B1C，与BC1相交于O，连接OD
∵BCC1B1是矩形，
∴O是B1C的中点.
又D是AC的中点，
∴OD//AB1.………………………………………………2分
∵AB1
面BDC1，OD
面BDC1，
∴AB1//面BDC1.…………………………………………4分
（II）解：如力，建立空间直角坐标系，则
C1（0，0，0），B（0，3，2），C（0，3，0），A（2，3，0），
D（1，3，0）……………………5分
|
=（x1，y1，z1）是面BDC1的一个法向量，则
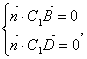
即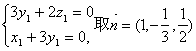
.…………6分
易知
=(0，3，0)是面ABC的一个法向量.
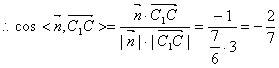.…………………………8分
∴二面角C1—BD—C的余弦值为
.………………………………9分
（III）假设侧棱AA1上存在一点P（2，y，0）（0≤y≤3），使得CP⊥面BDC1.
则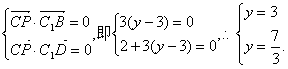
∴方程组无解.
∴假设不成立.……………………………………………………11分
∴侧棱AA1上不存在点P，使CP⊥面BDC1.…………………12分
19．（I）解：设答对题的个数为y，得分为ξ,y=0，1，2，4
∴ξ=0，2，4，8…………………………………………………………1分
……………………………………………………3分
…………………………………………5分
…………………………………………7分
………………………………………………9分
则ξ的分布列为
| ξ | 0 | 2 | 4 | 8 |
| P |
|
|
|
|
（II）Eξ=0×
+2×+4×+8×
=2
答：该人得分的期望为2分………………………………12分
20．解：
（I）由题意，令y=0，x<0，得f(x)[1－f(0)]=0，∵x<0时，f(x)>1.
∴1－f(0)=0. f(0)=1.…………………………………………………………2分
适合题意的f(x)的一个解析式为f(x)=()x.………………………………4分
（II）①由递推关系知f(an+1)·f(－2－an)=1，即f(an+1－2－an)=f(0).
∵f(x)的R上单调，∴an+1－an=2，（n∈N*），…………………………6分
又a1=1，故an=2n－1.……………………………………………………7分
②bn=
,Sn=b1+b2+…+bn=+()3+…+()2n－1
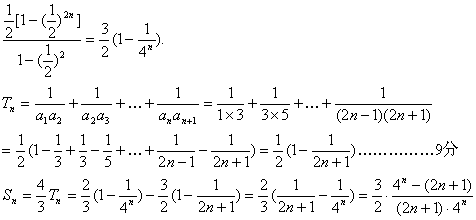
欲比较Sn与
的大小，只需比较4n与2n+1的大小.
由=1，2，3代入可知4n>2n+1，猜想4n>2n+1.……………………10分
下用数学归纳法证明
（i）当n=1时，41>2×1+1成立
（ii）假设当n=k时命题成立，即4k>2k+1
当n=k+1时，4k+1=4×4k>4(2k+1)=8k+4=2(k+1)+1+6k+1>2(k+1)+1，
说明当n=k+1时命题也成立.
由（i）（ii）可知，4n>2n+1 对于n∈N*都成立.
故Sn>.………………………………………………………………12分
注：证明4n>2n+1，除用数学归纳法证明以外，还可用其它方法证明，
如：4n=(1+3)n=1+
21．解：（I）定圆B的圆心坐标B（－，0），半径r=6，
因为动圆P与定圆B内切，所以PA+PB=6.
所以动圆圆心P的轨迹是以B、A为焦点，长轴长为6的椭圆.
|
设椭圆的方程为
则2a=6，a=3，c=
∴b2=a2－c2=4.
∴椭圆的方程为
.……………………4分
（II）设M(x1，y1)，N（x2，y2），
则由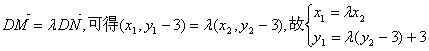
（1）当λ=1时，M与N重合，
，满足条件。
（2）当
.
综合可得λ的取值范围是[
，5].………………………………12分
22．解：
（I）f′(x)=3ax2+2bx－3，依题意，f′(1)=f′(－1)=0，
即
…………………………………………2分
解得a=1，b=0.
∴f(x)=x3－3x.……………………………………………………4分
（II）∵f(x)=x3－3x,∴f′(x)=3x2－3=3(x+1)(x－1)，
当－1<x<1时，f′(x)<0，故f(x)在区间[－1，1]上为减函数，
fmax(x)=f(－1)=2，fmin(x)=f(1)=－2……………………………………6分
∵对于区间[－1，1]上任意两个自变量的值x1，x2，
都有f(x1)－f(x2)≤fmax(x) －fmin(x)
f(x1)－f(x2)≤fmax(x)－fmin(x)=2－(－2)=4………………………………8分
（III）f′(x)=3x2－3=3(x+1)(x－1)，
∵曲线方程为y=x3－3x，∴点A（1，m）不在曲线上.
设切点为M（x0，y0），则点M的坐标满足
因
，故切线的斜率为
，
整理得
.
∵过点A（1，m）可作曲线的三条切线，
∴关于x0方程
=0有三个实根.……………………10分
设g(x0)= ，则g′(x0)=6
，
由g′(x0)=0，得x0=0或x0=1.
∴g(x0)在（－∞，0），（1，+∞）上单调递增，在（0，1）上单调递减.
∴函数g(x0)= 的极值点为x0=0，x0=1………………12分
∴关于x0方程=0有三个实根的充要条件是
，解得－3<m<－2.
故所求的实数a的取值范围是－3<m<－2.……………………14分