高三文科数学综合测试四

数学试题（文科）

本试卷分选择题和非选择题两部分，满分150分，考试用时120分钟。

注意事项：

1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的校名、姓名、考号填写在答题卡的密封线内。

2．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其它答案；不能答在试卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在别发的答题卷各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液，不按以上要求作答的答案无效。

4．考生必须保持答题卡的整洁，考试结束后，将答题卷和答题卡一并收回。

参考公式：

球的表面积公式　， 其中R表示球的半径

球的体积公式　　，其中R表示球的半径

第一部分（选择题，共50分）

一、本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．命题：“若”的逆否命题是　　　　　　　　　　　　　　　　（　　）

　　　 A．若

　　　 B．若

　　　 C．若

　　　 D．若

2．已知的虚部为　　　　　　　（　　）

　　　 A．1　　　　　　　　　　　　B．2　　　　　　　　　　　　C．i　　　　　　　　　　　　 D．2i

3．与函数的图象相同的函数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　　　　　B．

　　　 C．　　　　　　　　　　　　　　D．

4．下列函数中既是区间为周期的偶函数是　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　　　　 D．

5．正四棱锥底面边长为2，高为1，则此正四棱锥的侧面积等于　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　B．　　　　　　　　　C．　　　　　　　　　D．

6．直线的倾斜角为120°，则a的值是　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　 B．－　　　　　　　C．　　　　　　　　　D．－

7．给定两个向量a=(3,4)，b =(2,1)，若(a+xb)⊥(a－b)，则x等于　　　　　　　　　　　　　 （　　）

　　　 A．－3　　　　　　　　　　 B．　　　　　　　　　　　 C．3　　　　　　　　　　　　D．

8．已知有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．最小值　　　　　　　　　　　　　　　　　B．最大值

　　　 C．最小值　　　　　　　　　　　　　　　　　D．最大值

9．已知直线，若直线l₂经过点（0，5），且的方程为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　　　　　　　B．

　　　 C．　　　　　　　　　　　　　　　　　 D．

2,4,6

10．已知（a为常数）在[－2，2]上有最大值3，那么在[－2，2]上的最小值是　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．－5　　　　　　　　　　 B．－11　　　　　　　　　 C．－29　　　　　　　　　 D．－37

2,4,6

第二部分 （非选择题，共100分）

二、填空题：本大题共6小题，每小题5分，共30分。

11．在等比数列　　　　 ；

12．在一个水平放置的底面半径为的圆柱形量杯中装有适量的水，现放入一个半径为R的实心铁球，球完全浸没于水中且无水溢出，若水面高度恰好上升R，则R=　　　　。

13．在坐标平面内，由不等式组所确定的区域的面积为=　　　　 。

14．已知△ABC中，角A、B、C的对边分别为a、b、c，AH为BC边上的高，以下结论：

　　①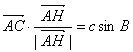　　　　　　　　　　　　　②

　　　 ③　　　　　　　 ④

　　其中正确的是　　　　　 。（写出所有你认为正确的结论的序号）

三、解答题：本大题共6小题，共80分。解答应定出文字说明、证明过程或演算步骤。

15．（本小题满分12分）

　　已知数列

　 （1）求数列的通项公式；

　 （2）求证数列是等比数列；

　 （3）求使得的集合。

16．（本小题满分12分）

　　已知A、B、C三点的坐标分别为、、

　 （1）若的值；

　 （2）若

17．（本小题满分14分）

　　　　一艘轮船在航行过程中的燃料费与它的速度的立方成正比例关系，其他与速度无关的费用每小时96元，已知在速度为每小时10公里时，每小时的燃料费是6元，要使行驶1公里所需的费用总和最小，这艘轮船的速度应确定为每小时多少公里？

18．（本小题满分14分）

　　如图，已知棱柱ABCD—A₁B₁C₁D₁的底面是菱形，且AA₁⊥面ABCD，∠DAB=60°，AD=AA₁，F为棱AA₁的中点，M为线段BD₁的中点。

　 （1）求证：MF∥面ABCD；

　 （2）求证：MF⊥面BDD₁B₁。

19．（本小题满分14分）

　　　　已知与曲线、y轴于、为原点。

　 （1）求证：；

　 （2）求线段AB中点的轨迹方程；

　 （3）求△AOB面积的最小值。

20．（本小题满分14分）

　　已知的定义域为区间[－1，1]。

　 （1）求函数的解析式；

　 （2）判断的单调性；

　 （3）若方程的取值范围。

参考答案

一、选择题

1．D　 2．A　 3．C　 4．B　 5．D　 6．A　 7．A　 8．A　 9．B　 10．D

2,4,6

二、填空题

11．40　　12．　 13．3　　14．①②③④

三、解答题

15．解：（1）设数列

由题意得：

解得：

　 （2）依题

，

为首项为2，公比为4的等比数列

　 （2）由

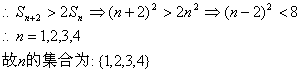
16．解：（1），

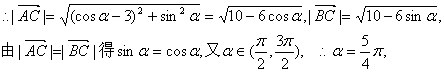
　 （2）由

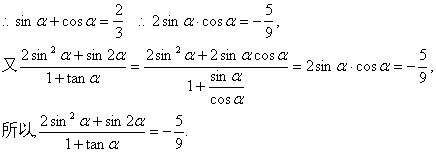
17．解法1：

设轮船的速度为x千米/小时（x>0），

则航行1公里的时间为小时。

依题意，设与速度有关的每小时燃料费用为，

答：轮船的速度应定为每小时20公里，行驶1公里所需的费用总和最小。

解法2：

设轮船的速度为x千米/小时（x>0），

则航行1公里的时间为小时，

依题意，设与速度有关的每小时燃料费用为

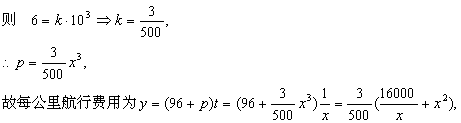
元，

且当时等号成立。

答：轮船的速度应定为每小时20公里，行驶1公里所需的费用总和最小。

18．证明：（1）连结AC、BD交于点O，再连结MO ，

　 （2）

　　

19．解：（1），半径为1依题设直线，

　　由圆C与l相切得：

　 （2）设线段AB中点为

　　代入即为所求的轨迹方程。

　 （3）

　　

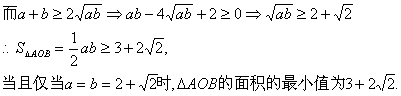
20．解：（1）

　 （2）

　 （3）由（2）知

在[－1，1]内有解