高三文科数学综合测试试题（三）

数学试题（文科）

本试卷分选择题和非选择题两部分，满分150分，考试用时120分钟.

注意事项：

1．答卷前，考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号填写在答题卡上，

　 用2B铅笔将试卷类型（A）填涂在答题卡上.

2．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改

　 动，用橡皮擦干净后，再选涂其它答案标号，不能答在试题卷上.

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区

　 域内的相应位置上；如需改动，先划掉原来的答案，然后写上新的答案；不准使用

　 铅笔和涂改液，不按以上要求作答的答案无效.

4．考生必须保持答题卡的整洁，考试结束后，将本试题卷和答题卡一并交回.

第Ⅰ卷（选择题，共50分）

一、（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的）

1．已知命题p：，则　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A． 　　　　　　　　　　　B．

　　　 C．　　　　　　　　　　　D．

2．函数的零点个数为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．0　　　　　　　　　　　　B．1　　　　　　　　　　　　C．2　　　　　　　　　　　　D．3

3．若的图象　　　　（　　）

　　　 A．关于直线y=x对称　　　　　　　　　　　　　　 B．关于x轴对称

　　　 C．关于y轴对称　　　　　　　　　　　　　　　　　　 D．关于原点对称

4．下列能使成立的所在区间是　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　 B．　　　　　　　C．　　　　　　　D．

5．下列四个函数中，以为最小正周期，且在区间上为减函数的是　　　　　 （　　）

　　　 A．　　　　B．　　　　C．　　　　D．

6．已知数列{a_n}中，a₁=2，前n项和S_n，若，则a_n=　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　B．　　　　　　　　 C．　　　　　　D．

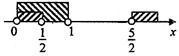
7．不等式的解集是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　　　　　　　 D．

8．已知函数，则a的所有可能值组成的集合为（　　）

　　　 A．　　　　　　 B． {1，}　　　　　C．{－}　　　　　　 D．{1}

9．设函数，则实数a的取值范围是　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　 B．（0，1）　　　　　　　C．　　　　　　　 D．

1,3,5

10．给出下面类比推理命题（其中Q为有理数集，R为实数集，C为复数集）：

　　①“若”类比推出“”

　②“若”类比推出

“”

③“若”类比推出“若”

　④“若”类比推出“若”

　其中类比结论正确的个数有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．1　　　　　　　　　　　　B．2　　　　　　　　　　　　C．3　　　　　　　　　　　　D．4

1,3,5

第Ⅱ卷（非选择题 共110分）

二、填空题：本大题共6小题，每小题5分，共30分）.

11．若复数z满足方程，则z=　　　　 

12．在等比数列{a_n}中，　　　

13．已知的最大值为　　　　　

14．将正整数排成下表：

　　1

　　2　　3　　4

　　5　　6　　7　　8　　9

　　10　 11　 12　 13　 14　 15　 16

　　……

则数表中的300应出现在第　　　　 行.

三、解答题；本大题共6小题，共80分. 解答应写出文字说明、证明过程或演算步骤.

15．（本小题满分12分）

　　已知a>0且

命题P：函数内单调递减；

命题Q：曲线轴交于不同的两点.

如果“P\/Q”为真且“P/\Q”为假，求a的取值范围.

16．（本小题满分12分）

某工厂生产甲、乙两种产品，已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额（量大供应量）如下表所示：

产品 消耗量 资源	甲产品（每吨）	乙产品（每吨）	资源限额（每天）
煤（t）	9	4	360
电力（kw·h）	4	5	200
劳动力（个）	3	10	300
利润（万元）	6	12

问：每天生产甲、乙两种产品各多少吨，获得利润总额最大？

17．（本小题满分14分）

在△ABC中，角A、B、C的对边分别为a、b、c. 已知

a+b=5，c=，

　 （1）求角C的大小；

　 （2）求△ABC的面积.

18．（本小题满分14分）

在公差为d（d≠0）的等差数列{a_n}和公比为q的等比数列{b_n}中，已知a₁=b₁=1，a₂=b₂，a₈=b₃.

　 （1）求数列{a_n}与{b_n}的通项公式；

　 （2）令，求数列{c_n}的前n项和T_n.

19．（本小题满分14分）

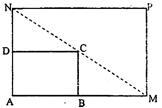
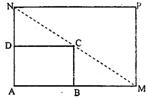
如图所示，将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN，要求B在AM上，D在AN上，且对角线MN过C点，AB=3米，AD=2米.

　 （Ⅰ）要使矩形AMPN的面积大于32平方米，则AM的长应在什么范围内？

　 （Ⅱ）当AM、AN的长度是多少时，矩形AMPN的面积最小？并求出最小面积.

20．（本小题满分14分）

定义域为R的偶函数，方程在R上恰有5个不同的实数解.

　 （Ⅰ）求x<0时，函数的解析式；

　 （Ⅱ）求实数a的取值范围.

　

参考答案

一、选择题

1,3,5

1．C

2．B 利用数形结合求解，令的交点个数.

3．C 解析：取满足可得答案C.

4．B 解析：取答案各区间的特点值代入检验即可.

5．D 解析：B、C的函数周期为2，不合题意，A的函数在区间上为增函数，不合题意

6．D 解析：由a₁=2知答案A不正确，再由a₁+a₂=S₂=4a_2­可得答案B、C不正确

7．A 解析：

　　 ，故选A.

8．A 解析：

　　 =2k+，故选A.

9．D 解析：满足

　　　，故a的取值范围是，故选D.

10．B 解析：①、②正确，③、④错误，因为③、④中对于虚数的情况没有大小关系，故选B.

二、填空题

11．答案：1－i　 解析：

12．答案：81　　 解析：

13．答案：　 解析：∵，当且仅当时取等号.

14．答案：18　　 解析：每行的数字取值从（n－1）²+1到n²，而17²<300<18²，故300在第18行.

三、解答题：

15．解：∵，

　　∴命题P为真时

命题P为假时

命题Q为真时，

命题Q为假时

由“P\/Q”为真且“P/\Q”为假，知P、Q有且只有一个正确.

情形（1）：P正确，且Q不正确

情形（2）：P不正确，且Q正确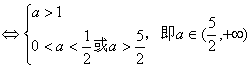

综上，a取值范围是

另解：依题意，命题P为真时，0<a<1

曲线轴交于两点等价于，

得 　故命题Q为真时，

由“P\/Q”为真且“P/\Q”为假，知P、Q有且只有一个正确.

等价于P、Q为真时在数轴表示图形中有且只有一个阴影的部分.

由图形知a取值范围是

（注：如果答案中端点取了开区间，扣2分）

16．解：设此工厂应分别生产甲、乙两种产品x吨、y吨. 获得利润z万元

依题意可得约束条件：　

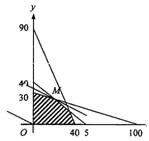
　　作出可行域如右图

利润目标函数z=6x+12y

由几何意义知当直线l：z=6x+12y，经过可行域上的点M时，z=6x+12y取最大值.

解方程组 ，得M（20，24）　

答：生产甲种产品20t，乙种产品24t，才能使此工厂获得最大利润

17．解：（Ⅰ）∵A+B+C=180°

　　由　

　　∴　

　　整理，得　　  解得：　

　　∵　　∴C=60°　

（Ⅱ）由余弦定理得：c²=a²+b²－2abcosC，即7=a²+b²－2ab

∴=25－3ab　

∴　

18．解：（1）由条件得：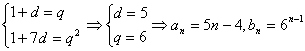　

（2） ①

∴6T_n=6+6×6²+11×6³+…+（5n－4）6ⁿ　②

①－②：

∴　

19．解：设AM的长为x米(x>3)

∵　 ∴

∴　…………3分

（Ⅰ）由S_AMPN>32得，

∵

即AM长的取值范围是（3，4）

（Ⅱ）令

∴当上单调递增，x<6，，函数在（3，6）上单调递减

∴当x=6时，取得最小值即S_AMPN取得最小值24（平方米）

此时AM=6米，AN=4米　

　　答：当AM、AN的长度分别是6米、4米时，矩形AMPN的面积最小，最小面积是24平方米.　　

　　另解：以AM、AN分别为x、y轴建立直角坐标系，

设

由C在直线MN上得

∴

∴AM的长取值范围是（3，4）

（Ⅱ）∵时等号成立.

∴AM=6米，AN=4米时，S_AMPN达到最小值24

答：当AM、AN的长度分别是6米、4米时，矩形AMPN的面积最小，最小面积是24平方米.

20．解：（1）设x<0，则－x>0

∵为偶函数，　∴

（2）∵为偶函数，∴=0的根关于0对称.

由=0恰有5个不同的实数解，知5个实根中有两个正根，二个负根，一个零根.

且两个正根和二个负根互为相反数

∴原命题图像与x轴恰有两个不同的交点

下面研究x>0时的情况

∵

即 为单调增函数，故不可能有两实根

∴a>0　令

当递减，

∴处取到极大值

又当

要使轴有两个交点当且仅当>0

解得，故实数a的取值范围（0，）

方法二：

（2）∵为偶函数， ∴=0的根关于0对称.

由=0恰有5个不同的实数解知5个实根中有两个正根，二个负根，一个零根.

且两个正根和二个负根互为相反数

∴原命题图像与x轴恰有两个不同的交点

下面研究x>0时的情况

与直线交点的个数.

∴当时，递增与直线y=ax下降或是x国，

故交点的个数为1，不合题意　∴a>0

由几何意义知与直线y=ax交点的个数为2时，直线y=ax的变化应是从x轴到与相切之间的情形.

设切点

∴切线方为　

由切线与y=ax重合知

故实数a的取值范围为（0，）