高三文科数学综合测试试题二

数学试题（文科）

选择题：本大题共10小题，每小题5分，共50分.

1．已知曲线的一条切线的斜率为，则切点的横坐标为　　　　　　　　　　　　　 （　　）

　　　 A．1　　　　　　　　　　　　B．2　　　　　　　　　　　　C．3　　　　　　　　　　　　D．4

2．若A　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．2　　　　　　　　　　　　B．±2　　　　　　　　　　 C．2、－2或0　　　　 D．2、－2、0或1

3．函数的最小正周期是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　B．4　　　　　　　　　　 C．　　　　　　　　　　　D．

4．若θ是第二象限的角，则下列四个值中，恒小于零的是　　　　　　　　　　　　　　　　　　 （　　）A．　　 B．　　　　　　　　　　　　　　　　C．　　　　　　　 D．cot

5．在各项都为正数的等比数列{a_n}中，a₁=3，前三项的和为21，则a₃+ a₄+ a₅=　　 （　　）

　　　 A．33　　　　　　　　　　　B．72　　　　　　　　　　　 C．84　　　　　　　　　　　D．189

6．已知上是单调增函数，则a的最大值是　　　　　　　　　　　 （　 ）

　　　 A．0　　　　　　　　　　　　B．1　　　　　　　　　　　　C．2　　　　　　　　　　　　D．3

7．已知定义在R上的函数是偶函数，对时，的值为　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．2　　　　　　　　　　　　B．－2　　　　　　　　　　 C．4　　　　　　　　　　　　D．－4

8．函数的图象是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

9．已知是定义在R上的奇函数，且为偶函数，对于函数有下列几种描述

　　　 ①是周期函数　　　　　　　　　　　　　 ②是它的一条对称轴

　　　 ③是它图象的一个对称中心　　　　 ④当时，它一定取最大值

　　其中描述正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．①②　　　　　　　　　 B．①③　　　　　　　　　 C．②④　　　　　　　　　 D．②③

2,4,6

10．已知上有最大值3，那么此函数在[－2，2]上的最小值为　　　　　　　　　 　　　　　　　　　　　　　　　　（　　）

　　　 A．－37　　　　　　　　　 B．－29　　　　　　　　　 C．－5　　　　　　　　　　 D．－11

二、填空题：本大题共4小题，每小题5分，共20分.

11．已知等差数列{a_n}前17项和S₁₇=51，则a₇+ a₁₁=　　　　　

12．在△ABC中，a²=b²+c²+bc，则角A=　　　　　  .

13．观察下列的图形中小正方形的个数，则第6个图中有　　　　  个小正方形。

14．规定一种运算：，例如：12=1，32=2，则函数的值域为　　　　　　　　 .

三、解答题：本大题共6小题，共80分，解答应写出文字说明、证明过程或演算步骤.

15．（本小题满分12分）

在数列

　 （Ⅰ）证明数列是等比数列；

　 （Ⅱ）求数列{}的前n项和S_n.

16．（本小题满分12分）

　　已知函数

　 （Ⅰ）当时，求的最小值；

　 （Ⅱ）若，求的单调区间。

17．（本小题满分14分）

　　已知函数。

　 （Ⅰ）若为奇函数，求a的值；

　 （Ⅱ）若在上恒大于0，求a的取值范围。

　　

18．（本小题满分14分）

　　如图，四边 形ABCD是一个边长为100米的正方形地皮，其中ATPS是一半径为90米的扇形小山，其余部分都是平地，P是弧TS上一点，现有一位开发商想在平地上建造一个两边落在BC与CD上的长方形停车场PQCR.

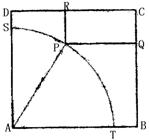
　 （Ⅰ）若∠PAT=θ，试写出四边形RPQC的面积S关于θ

　　　　 的函数表达式，并写出定义域；

　 （Ⅱ）试求停车场的面积最大值。

19．（本小题满分14分）

　　已知b>－1，c>0，函数的图象与函数的图象相切.

　 （Ⅰ）设

　 （Ⅱ）是否存在常数c，使得函数内有极值点？若存在，求出c的取值范围；若不存在，请说明理由.

20．（本小题满分14分）

　　　　已知函数，若存在，则称是函数的一个不动点，设

　 （Ⅰ）求函数的不动点；

　 （Ⅱ）对（Ⅰ）中的二个不动点a、b（假设a>b），求使恒成立的常数k的值；

　 （Ⅲ）对由a₁=1，a_n=定义的数列{a_n}，求其通项公式a_n.

参考答案

一、选择题

2,4,6

2,4,6

1．A　解析：斜率为2，所以x=1，故选A。

2．C　解析：由 不符合集合元素的互异性，故选C。

3．D　解析：

4．A　解析：由题可知，故选A.

5．C　解析：令公比为q，由a₁=3，前三项的和为21可得q²+q－6=0，各项都为正数，所以q=2，所以，故选C.

6．D 解析：上恒成立，即恒成立，故选D.

7．B　解析：因为定义在R上函数是偶函数，所以，故函数以4为周期，所以

8．C 解析：关于y轴的对称图形，可得的

图象，再向右平移一个单位，即可得的图象，即的图

象，故选C.

9．B　解析：可采取特例法，例皆为满足条件的函数，一一验证可知选B.

10．A　解析：故在[－2，2]上最大值为，所以最小值为，故选A.

二、填空题：

11．答案：6　 解析：∵　　 ∴a₇+a­₁₁=6.

12．答案A=120°　解析：

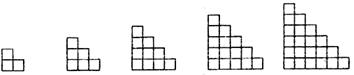
13．答案：28　解析：由前面图形规律知，第6个图中小正方形的数量为1+2+3+…+7=28。

14．答案：解：为a、b的最小值. 故可得为图象的实线曲线. 故当时，

三、解答题：

15．解：（Ⅰ），，　令

3m=1　　∴　　∴

∴{a_n+}是以为首项，4为公比的等比数列

（Ⅱ）　　  

∴

　　

16．解：（Ⅰ）

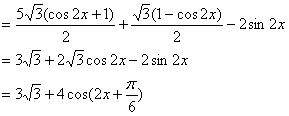
当时，的最小值为3－4

（Ⅱ）∵　　∴

∴

∴时，单调减区间为

17．解：（Ⅰ）的定义域关于原点对称

若为奇函数，则　∴a=0

（Ⅱ）

∴在上

∴在上单调递增

∴在上恒大于0只要大于0即可

∴

若在上恒大于0，a的取值范围为

18．解：（Ⅰ）延长RP交AB于M，设∠PAB=，则

AM =90

∴

　　　 =10000-

　

（Ⅱ）设　 ∵

∴

　　

∴当时，S_PQCR有最大值

答：长方形停车场PQCR面积的最磊值为平方米。

19．解：（Ⅰ）【方法一】由，

依题设可知，△=（b+1）²－4c=0.

∵.

∴

【方法二】依题设可知

∴为切点横坐标，

于是，化简得

同法一得

（Ⅱ）由

可得

令依题设欲使函数内有极值点，

则须满足

亦即 ，

又

故存在常数，使得函数内有极值点.

（注：若，则应扣1分. ）

20．解：（Ⅰ）设函数

　 （Ⅱ）由（Ⅰ）可知

可知使恒成立的常数k=8.

（Ⅲ）由（Ⅱ）知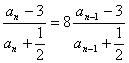　

可知数列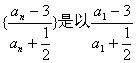为首项，8为公比的等比数列

即以为首项，8为公比的等比数列. 则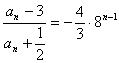　

.
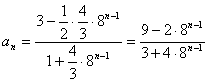