08届高三理科数学第三次阶段考试卷
一、选择题:本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是符合要求的.
1.若集合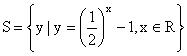 ,
,![]() ,则
,则![]() 等于( )
等于( )
A.{0} B.![]() C.S D.T
C.S D.T
2.等差数列![]() 的前n项和为
的前n项和为![]() ,那么下列S13值的是 ( )
,那么下列S13值的是 ( )
A.130 B.65 C.70 D.以上都不对
3、下列命题正确的是( )
A.函数![]() 在区间
在区间![]() 内单调递增
内单调递增
B.函数![]() 的最小正周期为
的最小正周期为![]()
C.函数![]() 的图像是关于点
的图像是关于点![]() 成中心对称的图形
成中心对称的图形
D.函数![]() 的图像是关于直线
的图像是关于直线![]() 成轴对称的图形
成轴对称的图形
4、在△ABC中,已知向量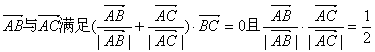 ,则△ABC为( ) ( )
,则△ABC为( ) ( )
A.三边均不相等的三角形 B.直角三角形
C.等腰非等边三角形 D.等边三角形
5、α、β为两个互相垂直的平面,a、b为一对异面直线,下列条件:①a//α、b![]() ;②a⊥α、b
;②a⊥α、b![]() ;③a⊥α、b
;③a⊥α、b![]() ;④a//α、b
;④a//α、b![]() 且a与α的距离等于b与β的距离,
且a与α的距离等于b与β的距离,
其中是a⊥b的充分条件的有 ( )
A.①④ B.① C.③ D.②③
 A、-1
B、1 C、0 D、0或±1
A、-1
B、1 C、0 D、0或±1
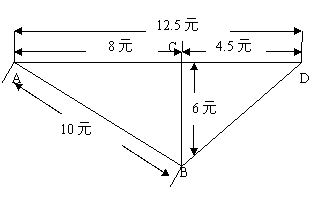 7、A,B,C,D四个城市之间有笔直的公路相连接,客运车行驶于各城市之间,其票价与路程成正比.具体票价如图
7、A,B,C,D四个城市之间有笔直的公路相连接,客运车行驶于各城市之间,其票价与路程成正比.具体票价如图
则BD之间的票价应为________
A、7元 B、7.5元
C、8元 D、8.5元
8、过抛物线y=![]() x2准线上任一点作抛物线的两条切线,若切点分别为M,N,则直线MN过定点( )
x2准线上任一点作抛物线的两条切线,若切点分别为M,N,则直线MN过定点( )
A、 (0,1) B、(1,0) C、(0,-1) D、(-1,0)
二、填空题:本大题共7小题,每小题5分,满分30分.其中13~15题是选做题,考生只能选做二题,三题全答的,只计算前两题得分.
9.若集合![]() ,若
,若![]() ,则实数a的取值范围是 .
,则实数a的取值范围是 .
10、已知△ABC的三个顶点A、B、C及所在平面内一点P满足![]() ,则点△BCP与△ABP的面积分别为s1,s2,则s1:s2=_________
,则点△BCP与△ABP的面积分别为s1,s2,则s1:s2=_________
11、数列![]() 满足
满足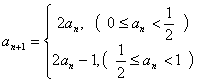 ,若
,若![]() ,则
,则![]() 的值为____
的值为____
12、球面上有3个点,其中任意两点的球面距离都等于大圆周长的![]() ,经过这3个点的小圆的周长为4π,那么这个球的直径为
,经过这3个点的小圆的周长为4π,那么这个球的直径为
13(选做题)、在直角坐标系中将曲线C1:xy=![]() 绕原点按逆时针方向旋转30°后得到曲线C2,则曲线C2截y轴所得的弦长为_______________________.
绕原点按逆时针方向旋转30°后得到曲线C2,则曲线C2截y轴所得的弦长为_______________________.
14(选做题)、已知不等式2x-4+3x+3+2x-1+2a-3<0的解集非空,则实数a的取值范围为_____________
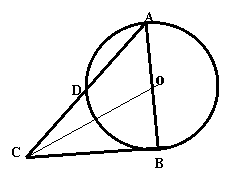
15(选做题)、如图,在⊙O中,AB为直径,AD为弦,过B点的切线与AD的延长线交于点C,且AD=DC,则sin∠ACO=_________
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.

17(13分)、已知{an}为等比数列,{bn}为等差数列,其中a2=b4,a3=b2,a4=b1,且a1=64,公比q≠1
(Ⅰ)求an,bn;
(Ⅱ)设cn=log2an,求数列{cnan}的前n项和Tn
![]()
![]()
|
 18(13分)、已知一几何体的三视图如图1,主视图与左视图为全等的等腰直角三角形,直角边长为6,俯视图为正方形,(1)求点A到面SBC的距离;(2)有一个小正四棱柱内接于这个几何体,棱柱底面在面ABCD内,其余顶点在几何体的棱上,当棱柱的底面边长与高取何值时,棱柱的体积最大,并求出这个最大值。
18(13分)、已知一几何体的三视图如图1,主视图与左视图为全等的等腰直角三角形,直角边长为6,俯视图为正方形,(1)求点A到面SBC的距离;(2)有一个小正四棱柱内接于这个几何体,棱柱底面在面ABCD内,其余顶点在几何体的棱上,当棱柱的底面边长与高取何值时,棱柱的体积最大,并求出这个最大值。
19、(14分)已知函数f(x)=ax3+x2-x (a∈R且a≠0)
(1)若函数f(x)在(2,+∞)上存在单调递增区间,求a的取值范围.
(2)证明:当a>0时,函数在f(x)在区间(![]() )上不存在零点
)上不存在零点
20、(14分)设不等式组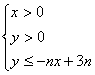 所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)的个数为f(n)(n∈N*).
所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)的个数为f(n)(n∈N*).
(1)求f(1)、f(2)的值及f(n)的表达式;(可以不作证明)
(2)记![]() ,若对于一切正整数n,总有Tn≤m成立,求实数m的取值
,若对于一切正整数n,总有Tn≤m成立,求实数m的取值
范围.
(3)(附加题,做对加4分)求证:当n∈N+时,![]()
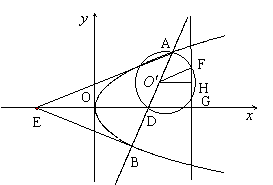
21、(14分)已知点H(-3,0),点P在![]() 轴上,点Q在
轴上,点Q在![]() 轴的正半轴上,点M在直线PQ上,且满足
轴的正半轴上,点M在直线PQ上,且满足![]() ,
, ![]()
![]() .
.
(Ⅰ)当点P在![]() 轴上移动时,求点M的轨迹C;
轴上移动时,求点M的轨迹C;
(Ⅱ)过定点![]() 作直线
作直线![]() 交轨迹C于A、B两点,E是D点关于坐标原点O的对称点,求证:
交轨迹C于A、B两点,E是D点关于坐标原点O的对称点,求证:![]() ;
;
 (Ⅲ)在(Ⅱ)中,是否存在垂直于
(Ⅲ)在(Ⅱ)中,是否存在垂直于![]() 轴的直线
轴的直线![]() 被以AD为直径的圆截得的弦长恒为定值?若存在求出
被以AD为直径的圆截得的弦长恒为定值?若存在求出![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
 答卷
答卷
| 题号 | 一 | 二 | 16 | 17 | 18 | 19 | 20 | 21 |
| 分数 |
二、填空题:本大题共7小题,每小题5分,满分30分.其中13~15题是选做题,考生只能选做二题,三题全答的,只计算前两题得分.
9、_________________________ 10、____________________________
11、_________________________ 12、____________________________
13、(选做题)__________________ 14、(选做题)____________________
15、(选做题)__________________
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤
16、
17、
 |
18、![]()
![]()
 19、
19、
20、
21、
参考答案
CACD CCBA
9、![]() 10、2:1 11、
10、2:1 11、![]() 12、
12、![]() 13、4
13、4
14、a<-1 15、![]()
16、
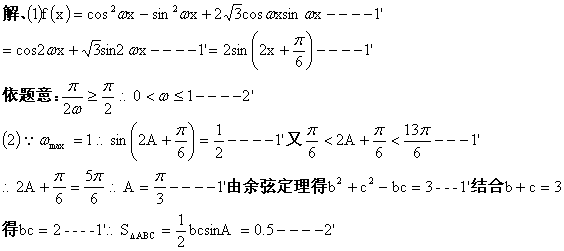 17、解:(I)依题意
17、解:(I)依题意![]()
![]() …………2分
…………2分
![]()
![]() …………4分
…………4分
![]() bn=8+8×(n-1)=8n …………5分
bn=8+8×(n-1)=8n …………5分
(II)![]() …………6分
…………6分

![]() …………12分
…………12分
18、(1)3![]()
(2)底面边长为2,高为4是,体积最大,最大体积为16
19、
略解、(1)因为f′(x)=3ax2+2x-1,依题意存在(2,+∞)的非空子区间使3ax2+2x-1>0成立,即![]() 在x∈(2,+∞)某子区间上恒成立,令h(x)=
在x∈(2,+∞)某子区间上恒成立,令h(x)=![]() ,求得h(x)的最小值为
,求得h(x)的最小值为![]() ,故
,故![]()
(2)由已知a>0
令f′(x)=3ax2+2x-1>0
得![]() 故f(x)在区间(
故f(x)在区间(![]() )上是减函数,
)上是减函数,![]() 即f(x)在区间(
即f(x)在区间(![]() )上恒大于零。故当a>0时,函数在f(x)在区间(
)上恒大于零。故当a>0时,函数在f(x)在区间(![]() )上不存在零点
)上不存在零点
20、(1)f(1)=3………………………………………………………………………………(1分)
f(2)=6………………………………………………………………………………(2分)
当x=1时,y=2n,可取格点2n个;当x=2时,y=n,可取格点n个
∴f(n)=3n…………………………………………………………………………(4分)
(2)![]() ………………………………………………(9分)
………………………………………………(9分)

∴T1<T2=T3>T4>…>Tn
故Tn的最大值是T2=T3=![]()
∴m≥![]() ………………………………………………………………()
………………………………………………………………()

21、解:(Ⅰ)设![]() ,
,
![]()
![]()
![]() 且
且![]() , …………………2分
, …………………2分
![]() …………………3分
…………………3分
![]() .
………………………………………………4分
.
………………………………………………4分
∴动点M的轨迹C是以O(0,0)为顶点,以(1,0)为焦点的抛物线(除去原点).
…………………………………………5分
(Ⅱ)解法一:(1)当直线![]() 垂直于
垂直于![]() 轴时,根据抛物线的对称性,有
轴时,根据抛物线的对称性,有![]() ;
;
……………6分
 (2)当直线
(2)当直线![]() 与
与![]() 轴不垂直时,依题意,可设直线
轴不垂直时,依题意,可设直线![]() 的方程为
的方程为![]() ,
,![]() ,则A,B两点的坐标满足方程组
,则A,B两点的坐标满足方程组
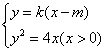
消去![]() 并整理,得
并整理,得
![]() ,
,
![]() . ……………7分
. ……………7分
设直线AE和BE的斜率分别为![]() ,则:
,则:
![]() =
=![]()
![]()
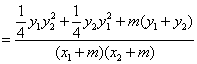
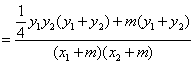
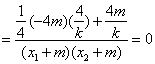 . …………………9分
. …………………9分
![]() ,
,
![]() ,
,
![]() ,
,![]()
![]() .
.
综合(1)、(2)可知![]() . …………………10分
. …………………10分
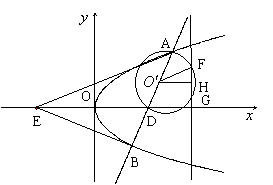 解法二:依题意,设直线
解法二:依题意,设直线![]() 的方程为
的方程为![]() ,
,![]() ,则A,B两点的坐标满足方程组:
,则A,B两点的坐标满足方程组:
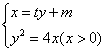
消去![]() 并整理,得
并整理,得
![]() ,
,
![]() . ……………7分
. ……………7分
设直线AE和BE的斜率分别为![]() ,则:
,则:
![]() =
=![]()
![]()
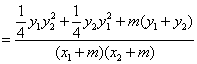
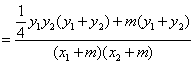
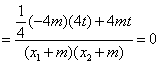 . …………………9分
. …………………9分
![]() ,
,
![]() ,
,
![]() ,
,![]()
![]() . ……………………………………………………10分
. ……………………………………………………10分
(Ⅲ)假设存在满足条件的直线![]() ,其方程为
,其方程为![]() ,AD的中点为
,AD的中点为![]() ,
,![]() 与AD为直径的圆相交于点F、G,FG的中点为H,则
与AD为直径的圆相交于点F、G,FG的中点为H,则![]() ,
,![]() 点的坐标为
点的坐标为![]() .
.
![]()
![]() ,
,
![]() ,
,
![]()
![]()
![]() .
…………………………12分
.
…………………………12分
![]() ,
,
令![]() ,得
,得![]()
此时,![]() .
.
∴当![]() ,即
,即![]() 时,
时,![]() (定值).
(定值).
∴当![]() 时,满足条件的直线
时,满足条件的直线![]() 存在,其方程为
存在,其方程为![]() ;当
;当![]() 时,满足条件的直线
时,满足条件的直线![]() 不存在.
不存在.