08届高三理科数学调研考试试题
本卷分选择题和非选择题两部分,满分150分.考试用时间120分钟.
注意事项:
1. 考生务必将自己的姓名、班级、学校用蓝、黑墨水钢笔签字笔写在答题卷上;
2. 选择题、填空题每小题得出答案后,请将答案填写在答题卷相应指定位置上。答在试题卷上不得分;
3. 考试结束,考生只需将答题案交回。
参考公式:锥体的体积公式![]() ,其中
,其中![]() 是锥体的底面积,
是锥体的底面积,![]() 是锥体的高.
是锥体的高.
如果事件![]() 、
、![]() 互斥,那么
互斥,那么![]() .
.
如果事件![]() 、
、![]() 相互独立,那么
相互独立,那么![]() .
.
第一部分 选择题(共40分)
一、选择题(本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 已知复数![]() ,则
,则![]()
A. ![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
2. 设全集![]() 且
且![]() ,
,![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3. 椭圆![]() 的焦点在
的焦点在![]() 轴上,长轴长是短轴长的两倍,则
轴上,长轴长是短轴长的两倍,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C. 2 D.4
C. 2 D.4
4. ![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]()
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]() 或
或![]()
5. 已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,则过点
,则过点![]() 和
和![]()
![]() N*)的直线的斜率是
N*)的直线的斜率是
A.4 B.3 C.2 D.1
 6.已知函数
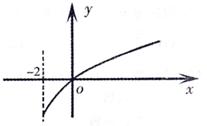
6.已知函数![]() ,且
,且![]() ,
,![]() 的导函数,函数
的导函数,函数![]() 的图象如图所示. 则平面区域
的图象如图所示. 则平面区域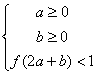 所围成的面积是
所围成的面积是
A.2 B.4 C.5 D.8
7. 一台机床有![]() 的时间加工零件A, 其余时间加工零件B, 加工A时,停机的概率是
的时间加工零件A, 其余时间加工零件B, 加工A时,停机的概率是![]() ,
,
加工B时,停机的概率是![]() , 则这台机床停机的概率为( )
, 则这台机床停机的概率为( )
A.
![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
8.
在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点,如果函数![]() 的图象恰好通过
的图象恰好通过![]() 个整点,则称函数
个整点,则称函数![]() 为
为![]() 阶整点函数。有下列函数:
阶整点函数。有下列函数:
① ![]() ; ②
; ②![]() ③
③![]() ④
④![]() ,
,
其中是一阶整点函数的是( )
A.①②③④ B.①③④ C.①④ D.④
第二部分 非选择题(共110分)
二.填空题(每小题5分,共30分)
 9. 若奇函数
9. 若奇函数![]() 的定义域为
的定义域为![]() ,则
,则![]() =
=
10. 计算![]()
11.已知正三角形内切圆的半径是高的![]() ,把这个结论推广到空间正四面体,类似的结论是____________________.
,把这个结论推广到空间正四面体,类似的结论是____________________.
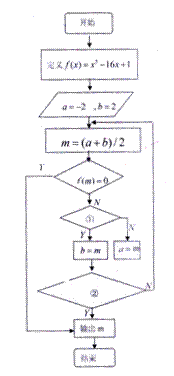
12.右图是用二分法求方程![]() 在
在![]() 的近似解的程序框图,要求解的精确度为
的近似解的程序框图,要求解的精确度为![]() ,①处填的内容是____________, ②处填的内容是______________________.
,①处填的内容是____________, ②处填的内容是______________________.
第13至15题,从3题中选答2题,多选按前2题记分
13. 设M、N分别是曲线![]() 和
和![]() 上的动点,则M、N的最小距离是
上的动点,则M、N的最小距离是
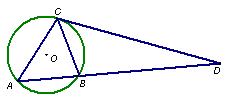
14. 如图,圆![]() 是
是![]() 的外接圆,过点C的切线交
的外接圆,过点C的切线交![]() 的延长线于点
的延长线于点![]() ,
,![]() ,
,![]() 。则
。则![]() 的长______________,
的长______________,![]() 的长______________.
的长______________.
 15. 已知
15. 已知![]() 且
且![]() ,
,
则![]() .
.
16.(本题满分12分)
 某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段![]() ,
,![]() …
…![]() 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求第四小组的频率,并补全这个频率分布直方图;
(Ⅱ)估计这次考试的及格率(60分及以上为及格)和
平均分;
(Ⅲ) 从成绩是70分以上(包括70分)的学生中选两人,
求他们在同一分数段的概率.
17.(本题满分12分)
已知![]()
![]() ,
,
(Ⅰ)求函数![]() 的最小正周期;
的最小正周期;
(Ⅱ) 当![]() ,求函数
,求函数![]() 的零点.
的零点.
18. (本题满分14分)
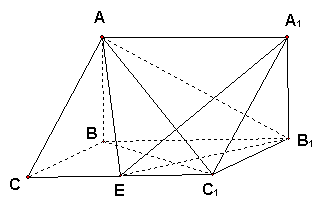
如图,在三棱拄![]() 中,
中,![]() 侧面
侧面![]() ,已知
,已知![]()
![]()
(Ⅰ)求证:![]() ;
;
(Ⅱ)试在棱![]() (不包含端点
(不包含端点![]() 上确定一点
上确定一点![]() 的位置,使得
的位置,使得![]() ;
;
(Ⅲ) 在(Ⅱ)的条件下,求二面角![]() 的平面角的正切值.
的平面角的正切值.
19. (本题满分14分)
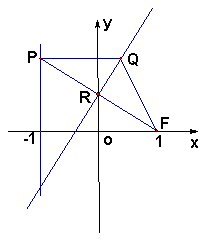 在平面直角坐标系
在平面直角坐标系![]() 中,设点
中,设点![]() (1,0),直线
(1,0),直线![]() :
:![]() ,点
,点![]() 在直线
在直线![]() 上移动,
上移动,![]() 是线段
是线段![]() 与
与![]() 轴的交点,
轴的交点, ![]() .
.
(Ⅰ)求动点![]() 的轨迹的方程;
的轨迹的方程;
(Ⅱ) 记![]() 的轨迹的方程为
的轨迹的方程为![]() ,过点
,过点![]() 作两条互相垂直的曲线
作两条互相垂直的曲线![]() 的弦
的弦![]() 、
、![]() ,设
,设![]() 、
、![]() 的中点分别为
的中点分别为![]() .求证:直线
.求证:直线![]() 必过定点
必过定点![]() .
.
20.(本题满分14分)
已知数列![]() 中,
中,![]() ,且
,且![]()
(Ⅰ)求证:![]()
![]() ;
;
(Ⅱ)设![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,求
项和,求![]() 的解析式;
的解析式;
(Ⅲ)求证:不等式![]() 对
对![]() 恒成立.
恒成立.
21. (本题满分14分)
已知函数![]() (其中
(其中![]() ) ,
) ,
点![]() 从左到右依次是函数
从左到右依次是函数![]() 图象上三点,且
图象上三点,且![]() .
.
(Ⅰ) 证明: 函数![]() 在
在![]() 上是减函数;
上是减函数;
(Ⅱ)
求证:⊿![]() 是钝角三角形;
是钝角三角形;
(Ⅲ) 试问,⊿![]() 能否是等腰三角形?若能,求⊿
能否是等腰三角形?若能,求⊿![]() 面积的最大值;若不能,请说明理由.
面积的最大值;若不能,请说明理由.