08届高三数学（理科）高考模拟题

第一部分 选择题（共40分）

一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的

1、设集合，，那么“”是“”的（　  ）

A．充分而不必要条件 　 　　　　　　　B．必要而不充分条件

C．充分必要条件　  　　　　　　　 　 D．既不充分也不必要条件

2、　　　　　　　　　  (　　)

　　　 A．　　　　　　　　B．　　　　　 C． 　　　　D．

3、若展开式中的所有二项式系数和为512，则该展开式中的常数项为　　 （　　）

A. －84 　　 B. 　　　 C. －36　　　 D.

4、如果复数是实数，则实数　　　　　　　　　　　　　　　  （　　）

A．　　　　　　　 B．　　　　　 C．　　　　　　 D．

5、下列各组命题中，满足“‘p或q’为真、‘p且q’为假、‘非p’为真”的是　　 ( 　　)

A.　p：；　　q：.

B.　p：在△ABC中，若，则；

q：在第一象限是增函数.

C.　p：；

q：不等式的解集是.

D.　p：圆的面积被直线平分；

q：椭圆的一条准线方程是.

6、右图给出的是计算的值的一个程序框图，其中判断框内应填入的条件是（　　 ）

A.i>10　 B.i<10　C.i>20　D.i<20

7、函数的值域是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（ 　 ）

　　A．　　　　　　　　 B．　　　　　　　　C．　　　　　　　　 D．

8、已知椭圆的左焦点为，为椭圆的两个顶点，若到的距离等于，则椭圆的离心率为　　　　　　　　　　　　　　 （　　）

　　A. 　　　　　　　　 B. 　　　　　　　　 C. 　　　　　　　　　　　D.

第二部分 非选择题（共110分）

二、填空题（本大题共6小题，共30分，把答案填写在答题卡相应位置上）

9、若，则； .

10、若 ，则目标函数的取值范围是　　　　　

11、（从以下三题中选做两题，如有多选，按得分最低的两题记分.）

（A）

则___________

（B）若不等式x-2+x+3<的解集为Æ,则的取值范围为_____________.

（C）参数方程(是参数)表示的曲线的普通方程是_________________.

12、设定义在R上的偶函数f(x)满足f(x+1)+f(x)=1,且当x∈［1,2］时，f(x)=2－x,则=_________.

13、观察下列的图形中小正方形的个数，则第6个图中有_______个小正方形，第n个图中有　　　　　　　 ________________个小正方形.

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

三、解答题（有6大道题，共80分，要求写出推理和运算的过程）

14、(本题满分12分)

已知向量，, 定义.

（Ⅰ）求函数的最小正周期；

（Ⅱ）若，当时，求的取值范围.

15、（本小题满分12分）

如图，棱锥P—ABCD的底面ABCD是矩形，PA⊥平面ABCD，PA=AD=2，BD=.

（Ⅰ）求证：BD⊥平面PAC；

（Ⅱ）求二面角P—CD—B的大小；

（Ⅲ）求点C到平面PBD的距离.

16、（本小题满分14分）

甲、乙两人各射击一次，击中目标的概率分别是和.假设两人射击是否击中目标，相互之间没有影响；每次射击是否击中目标，相互之间没有影响.

(Ⅰ)求甲射击4次,至少1次未击中目标的概率;

(Ⅱ)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;

(Ⅲ)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少?

17、（本小题满分14分）

设各项为正数的等比数列的首项，前n项和为，且。

（Ⅰ）求的通项；

（Ⅱ）求的前n项和。

18、（本小题满分14分）

已知函数的图象为曲线E.

(Ⅰ) 若曲线E上存在点P，使曲线E在P点处的切线与x轴平行，求a,b的关系；

(Ⅱ) 说明函数可以在和时取得极值，并求此时a,b的值；

(Ⅲ) 在满足(2)的条件下，在恒成立，求c的取值范围.

19、(本小题满分14分)

已知椭圆的一个焦点，对应的准线方程为，且离心率满足，，成等比数列.

(1)求椭圆的方程；

(2)试问是否存在直线，使与椭圆交于不同的两点、，且线段恰被直线平分？若存在，求出的倾斜角的取值范围；若不存在，请说明理由.

答题卷

题  号	一	二	三						总  分
			15	16	17	18	19	20
得  分

一、选择题（本大题共8小题，每小题5分，共40分；在每小题给出的四个选项中，只有一项是符合题目要求的.）

题号	1	2	3	4	5	6	7	8
答案

二、填空题（本大题6小题，每小题5分，共30分）

9、　 　　；_______ 10、　　　　 ；11、（A）________;（B）　　　　；（C）_____________;　　12、_________________.13、____________;_______________.

三、解答题（本大题共6小题，共80分。解答应写出文字说明、证明过程或演算步骤）

14

15

16

17

18

19

参考答案

第Ⅰ卷

一、选择题

题号	1	2	3	4	5	6	7	8
答案	B	B	B	A	C	A	D	C

第Ⅱ卷

二、填空题

9、3 , ;　　10、;　　 11、（A）; （B）；（C）();　　12、0.5　　　 13、28 ,

三、解答题

14、（本小题满分12分）

解：（Ⅰ）＝

　　　　　　　　　　　 ＝+

　　　　　　　　　　　 ＝+

　　所以，的最小正周期　

(Ⅱ)

　　　

由三角函数图象知:

的取值范围是

15、（本小题满分12分）

方法一：

证：（Ⅰ）在Rt△BAD中，AD=2，BD=，

∴AB=2，ABCD为正方形，

因此BD⊥AC.　　　　　　　　　　

∵PA⊥平面ABCD，BDÌ平面ABCD，

∴BD⊥PA .　　　　　　　　　　　

又∵PA∩AC=A

∴BD⊥平面PAC.　　　　　　　　 

解：（Ⅱ）由PA⊥面ABCD，知AD为PD在平面ABCD的射影，又CD⊥AD，

∴CD⊥PD，知∠PDA为二面角P—CD—B的平面角.　　　　　　　　　　　

又∵PA=AD，

∴∠PDA=45⁰ .　　　　　　　　　　　　　　　　　　　　　　　　　　　 

（Ⅲ）∵PA=AB=AD=2

∴PB=PD=BD=

设C到面PBD的距离为d，由，

有，　　　　　　　　　　　　　　　

即，

得　　　　 

方法二：

证：（Ⅰ）建立如图所示的直角坐标系，

则A（0，0，0）、D（0，2，0）、P（0，0，2）.

在Rt△BAD中，AD=2，BD=，

∴AB=2.

∴B（2，0，0）、C（2，2，0），

∴　

∵

即BD⊥AP，BD⊥AC，又AP∩AC=A，

∴BD⊥平面PAC.　　　　　　　　　　　 

解：（Ⅱ）由（Ⅰ）得.

设平面PCD的法向量为，则，

即，∴

故平面PCD的法向量可取为　　　　　　　　　　　　　　　

∵PA⊥平面ABCD，∴为平面ABCD的法向量.　　　　　　 

设二面角P—CD—B的大小为q，依题意可得，

∴q = 45⁰ .　　　　　　　　　　　　　　　　　　　　　　　　 　　　

（Ⅲ）由（Ⅰ）得

设平面PBD的法向量为，则，

即，∴x=y=z

故平面PBD的法向量可取为.　　　　　　　　　　　　　　 

∵，

∴C到面PBD的距离为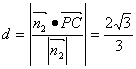　　　　　　　　　　　　　

16、（本小题满分14分）

解：（1）设“甲射击4次，至少1次未击中目标”为事件A，则其对立事件为“4次均击中目标”，则

（2）设“甲恰好击中目标2次且乙恰好击中目标3次”为事件B,则

（3）设“乙恰好射击5次后，被中止射击”为事件C,由于乙恰好射击5次后被中止射击,故必然是最后两次未击中目标，第三次击中目标，第一次及第二次至多有一次未击中目标。

故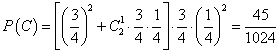

17、（本小题满分14分）

解：（Ⅰ）由  得

即

可得

因为，所以 　解得，因而

 （Ⅱ）因为是首项、公比的等比数列，故

则数列的前n项和

前两式相减，得　

　 即　

18、（本小题满分14分）

解：(1) ,设切点为,则曲线在点P的切线的斜率,由题意知有解，

∴即.

 (2)若函数可以在和时取得极值，

则有两个解和，且满足.

易得.

(3)由(2)，得.

根据题意，()恒成立.

∵函数（）在时有极大值（用求导的方法），

且在端点处的值为.

∴函数（）的最大值为.　

所以.

19、（本小题满分14分）

解：（1）∵成等比数列　∴　

设是椭圆上任意一点，依椭圆的定义得

 

即为所求的椭圆方程.

（2）假设存在，因与直线相交，不可能垂直轴

因此可设的方程为：由

　 ①

方程①有两个不等的实数根

∴　②

设两个交点、的坐标分别为　∴

∵线段恰被直线平分　∴

∵　∴ ③　把③代入②得

∵　 ∴　∴解得或

∴直线的倾斜角范围为