高三数学（理科）第一学期期末五校联考试题

第一部分　选择题（共40分）

一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个是符合题目要求的．

1．若集合，，则=

A．　　 　B．　　　　C．　　　　D．

2．在复平面内，复数 对应的点位于

A．第一象限  　 B．第二象限　　　　　　C．第三象限　 　　D．第四象限

3．已知，则的值等于　　

A．　　　　　 B．1　　　　　　  C．2　　　　　　  D．3

4．已知三条不重合的直线m、n、l，两个不重合的平面，有下列命题

①若；　　　　　  ②若；

③若； ④若；

其中正确的命题个数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

A．1　　　　　　　　　　　　　B．2　　　　　　　　　　　　　C．3　　　　　　　　　　　　D．4

5．已知数列、都是公差为1的等差数列，其首项分别为、，且，，，则数列前10项的和等于

A.55　　　　　　　B.70　　　　　　　　C.85　　　　　　　D.100

6．定义行列式运算=. 将函数的图象向左平移（）个单位,所得图象对应的函数为偶函数，则的最小值为　　

　　A．　　　　　　　　　　 B．　　　　　　　　　　　C．　　　　　　　　　 D．

7．定义在上的函数的图象关于点成中心对称，对任意的实数都有，且，则的值为

　　A．　　　　　　　　　 B．　　　　　　　　　C．0　　　　　　　　　　　　D．1

8．对任意正整数，定义的双阶乘如下：

当为偶数时，

当为奇数时，`

现有四个命题：①，　②，

③个位数为0，　　　　 ④个位数为5

其中正确的个数为

A.1　  　　　　　　B.2 　　　　　　　C.3 　　　　　　　 D.4

第二部分 非选择题（共110分）

二、填空题：本大题共7小题，其中9～12题是必做题,13～15题是选做题. 每小题5分，满分30分.

9．若抛物线的焦点与双曲线的右焦点重合，则的值为　　　　　 ．

10．设＝，则二项式展开式中含项的系数是　　　　　　　　　　　　

11．在Rt△ABC中，CA⊥CB，斜边AB上的高为h₁，

则；类比此性质，如图，在四

面体P—ABC中，若PA，PB，PC两两垂直，底

面ABC上的高为h，则得到的正确结论为　　　　　　　　　　　　　　　　　 ；

12．某医疗研究所为了检验某种血清预防感冒的作用，把名使用血清的人与另外名未用血清的人一年中的感冒记录作比较，提出假设：“这种血清不能起到预防感冒的作用”，利用列联表计算得，经查对临界值表知．

对此，四名同学做出了以下的判断：

p：有的把握认为“这种血清能起到预防感冒的作用”

q：若某人未使用该血清，那么他在一年中有的可能性得感冒

r：这种血清预防感冒的有效率为　　

s：这种血清预防感冒的有效率为　

则下列结论中，正确结论的序号是　　　　　 ．（把你认为正确的命题序号都填上）

（1）　p∧﹁q ；　　　　　　　 （2）﹁p∧q ；　　　　

(3)（﹁p∧﹁q）∧（r∨s）；　 （4）(p∨﹁r)∧(﹁q∨s)

▲选做题:在下面三道小题中选做两题,三题都选的只计算前两题的得分.

13．（坐标系与参数方程选做题） 已知圆的极坐标方程为，则该圆的圆心到直线 的距离是　　　　　　　　  .

14．（不等式选讲选做题） 已知g(x)=x-1-x-2,则g(x)的值域为　　　　　　　　　  ；

若关于的不等式的解集为空集，则实数的取值范围是　　　　　　　　 ．　　　　　　　

15．（几何证明选讲选做题） 如图：PA与圆O相切于A，

PCB为圆O的割线，并且不过圆心O，已知∠BPA=，

PA=，PC=1，则圆O的半径等于　　　　　　　  ．

三、解答题：本大题共6小题，共80分．解答应写出文字说明、演算步骤或推证过程.

16．（本小题满分12分）  在△ABC中，角A、B、C的对边分别为a、b、c.已知a+b=5，c =，且　　(1) 求角C的大小； 　 （2）求△ABC的面积.

17．（本小题满分12分）一个盒子装有六张卡片，上面分别写着如下六个定义域为R的函数：

（1）现从盒子中任取两张卡片，将卡片上的函数相加得一个新函数，求所得函数是奇函数的概率；

（2）现从盒子中进行逐一抽取卡片，且每次取出后均不放回，若取到一张记有偶函数的卡片则停止抽取，否则继续进行，求抽取次数的分布列和数学期望.

18．(本小题满分14分) 已知梯形ABCD中，AD∥BC，∠ABC =∠BAD =，AB=BC=2AD=4，E、F分别是AB、CD上的点，EF∥BC，AE = x，G是BC的中点。沿EF将梯形ABCD翻折，使平面AEFD⊥平面EBCF (如图) .

(1) 当x=2时，求证：BD⊥EG ；

(2) 若以F、B、C、D为顶点的三棱锥的体积记为f(x)，求f(x)的最大值；

(3) 当 f(x)取得最大值时，求二面角D-BF-C的余弦值.

19．(本小题满分14分) 椭圆C的中心为坐标原点O，焦点在y轴上，离心率e = ，椭圆上的点到焦点的最短距离为1-e, 直线l与y轴交于点P（0，m），与椭圆C交于相异两点A、B，且．（1）求椭圆方程；　（2）若，求m的取值范围．

20．(本小题满分14分)已知数列的前n项和满足：（a为常数，且）．　（Ⅰ）求的通项公式；

（Ⅱ）设，若数列为等比数列，求a的值；

（Ⅲ）在满足条件（Ⅱ）的情形下，设，数列的前n项和为T_n .

求证：．

21．(本小题满分14分) 已知函数

（I）若 在其定义域是增函数，求b的取值范围；

（II）在（I）的结论下，设函数的最小值；

（III）设函数的图象C₁与函数的图象C₂交于点P、Q，过线段PQ的中点R作x轴的垂线分别交C₁、C₂于点M、N，问是否存在点R，使C₁在M处的切线与C₂在N处的切线平行？若存在，求出R的横坐标；若不存在，请说明理由.

试题答案

一、选择题：（本大题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。）

题号	1	2	3	4	5	6	7	8
答案	B	B	D	B	C	C	D	C

1、解析： B．本题考查了定义域及交集运算

={-1＜x＜1},　N={0≤x＜1}　

2． 解析：B．本题考查了复数的概念及运算

  原式=

3．解析：D．本题考查了函数概念及分段函数

4．解析：B．本题考查了直线和平面的基本位置关系．

②，④正确；①，③错误

5．解析：C．本题考查了等差数列的通项及前项和计算．

因此，数列 也是等差数列，并且前10项和等于：

6． 解析：C．本题考查了信息的处理、迁移和应用能力以及三角函数的基础知识．

=2cos(x+)　　左移 n　　　 2cos(x+n+)　,  因此，n=

7． 解析：D．本题考查了函数的对称性和周期性．

由，得，因此，是周期函数，并且周期是３

函数的图象关于点成中心对称, 因此，=-，所以，

，＝

8．解析：C．本题考查了信息处理和应用能力．

因为　

所以，有

因此，①，③，④正确；②错误

第二部分 非选择题（共110分）

二、填空题：本大题共7小题，其中9～12题是必做题,13～15题是选做题. 每小题5分，满分30分.

9．　解析：６．本题考查了抛物线和双曲线的有关基本知识．

双曲线的右焦点F（3,0）是抛物线的焦点，所以，，p=6

10．解析：－192．本题考查了简单定积分的计算以及求二项式展开式的指定项的基本方法．

＝=2 ,　T=(-1) ()()=(-1) 2x

令３－r=2,得r=1 , 因此，展开式中含项的系数是－192．

11．解析：．本题考查了合情推理的能力．

连接CO且延长交AB于点D，连PD，

由已知PC⊥PD，在直角三角形PDC中，DC·h＝PD·PC，

即，

容易知道 AB⊥平面PDC，所以AB⊥PD，

在直角三角形APB中，AB·PD＝PA·PB，所以，

，故。

（也可以由等体积法得到）

12．解析：（1）（4）．本题考查了独立性检验的基本思想及常用逻辑用语．由题意，得，，所以，只有第一位同学的判断正确，即：有的把握认为“这种血清能起到预防感冒的作用”．由真值表知（1）（4）为真命题．

▲选做题:在下面三道小题中选做两题,三题都选的只计算前两题的得分.（其中14题第一空3分，第二空2分）

13．解析：．本题考查了简单的直线和圆的极坐标方程以及它们的基本知识．

直线 化为直角坐标方程是2x+y-1=0; 圆的圆心（１，０）

到直线2x+y-1=0的距离是

14． 解析：  [－１，１] ； ．本题考查绝对值的意义，含参绝对值不等式的解法．

当x≤1时，g(x)=x-1-x-2=-1

当１＜x≤２时，g(x)=x-1-x-2=2x-3,所以-１<≤1

当x＞２时，g(x)=x-1-x-2=1

_{综合以上，知-1≤g(x) ≤1。}

（此结果也可以由绝对值的几何意义直接得出）

的解集为空集，就是1= []_max＜

_所以　.

15．解析：7．本题考查了圆和切线的基本知识．

由圆的性质PA=PC·PB，得，PB=12，连接OA并反向延长

交圆于点E，在直角三角形APD中可以求得PD=4,DA=2,故CD=3,

DB=8,J记圆的半径为R,由于ED·DA=CD·DB

因此，(２R－２) ·2=3·8,解得R=7

三、解答题：

16．（本小题满分12分）

(1) 解：∵A+B+C=180°

　　由　…………1分

　　∴　 ………………3分

　　整理，得　 …………4分

解 得：　 ……5分

　　∵　∴C=60°　 ………………6分

（2）解：由余弦定理得：c²=a²+b²－2abcosC，即7=a²+b²－ab　…………7分

∴　 ………………8分　

由条件a+b=5得 7=25－3ab …… 9分　　　

……10分

∴　 …………12分

17．（本小题满分12分）

解：（1）记事件A为“任取两张卡片，将卡片上的函数相加得到的函数是奇函数”，由题意知 ………………………………………………………………4分

　 （2）ξ可取1，2，3，4.

　　，

　　； …………8分

　　故ξ的分布列为

ξ	1	2	3	4
P

　　　　　　　　　　　　　  ……………………………………………………………10分

　　

　　答：ξ的数学期望为 ………………………………………………………………12分

18．（本小题满分14分）

解:（1）（法一）∵平面平面,AE⊥EF,∴AE⊥面平面,AE⊥EF,AE⊥BE,又BE⊥EF,故可如图建立空间坐标系E-xyz。…………………………………………… 1分

则A（0，0，2），B（2，0，0），G（2，2，0），D（0，2，2），E（0，0，0）…………2分

（－2，2，2），（2，2，0）…………………………………………………3分

（－2，2，2）（2，2，0）＝0，∴ ……………………………4分

（法二）作DH⊥EF于H，连BH，GH，……………1分

由平面平面知：DH⊥平面EBCF，

而EG平面EBCF，故EG⊥DH。

又四边形BGHE为正方形，∴EG⊥BH，

BHDH＝H，故EG⊥平面DBH，………………… 3分

而BD平面DBH，∴ EG⊥BD。………………… 4分

（或者直接利用三垂线定理得出结果）

（2）∵AD∥面BFC，

所以 V_A-BFC＝＝4(4-x)x

………………………………………………………………………7分

即时有最大值为。…………………………………………………………8分

（3）（法一）设平面DBF的法向量为，∵AE=2, B（2，0，0），D（0，2，2），

F（0，3，0）,∴（－2，2，2）, ………………………………9分

则 ，

即，

取x＝3，则y＝2，z＝1，∴　

 面BCF的一个法向量为　　　　 ……………………………12分

则cos<>= 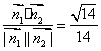 …………………………………………13分

由于所求二面角D-BF-C的平面角为钝角，所以此二面角的余弦值为－ ………………………………………………………………………………14分

（法二）作DH⊥EF于H，作HM⊥BF，连DM。

由三垂线定理知 BF⊥DM，∴∠DMH是二面角D-BF-C的平面角的补角。　　　　　　 ………………………………………………………………9分

由△HMF∽△EBF，知，而HF=1，BE=2，，∴HM＝。

又DH＝2，

∴在Rt△HMD中，tan∠DMH=-，

因∠DMH为锐角，∴cos∠DMH＝，　………………………………13分

而∠DMH是二面角D-BF-C的平面角的补角，

故二面角D-BF-C的余弦值为－。　　 ………………………………14分

19．（本小题满分14分）

 解：（1）设C：＋＝1（a>b>0），设c>0，c²＝a²－b²，由条件知a-c＝，＝，

∴a＝1，b＝c＝，

故C的方程为：y²＋＝1　　　 ………………………………………4分

（2）由＝λ得－＝λ（－），（1＋λ）＝＋λ，

∴λ＋1＝4，λ＝3　　　　　　  ………………………………………………6分

设l与椭圆C交点为A（x₁，y₁），B（x₂，y₂）

得（k²＋2）x²＋2kmx＋（m²－1）＝0

Δ＝（2km）²－4（k²＋2）（m²－1）＝4（k²－2m²＋2）>0 （*）

x₁＋x₂＝， x₁x₂＝　　………………………………………………9分

∵＝3 ∴－x₁＝3x₂ ∴

消去x₂，得3（x₁＋x₂）²＋4x₁x₂＝0，∴3（）²＋4＝0

整理得4k²m²＋2m²－k²－2＝0　　………………………………………………11分

m²＝时，上式不成立；m²≠时，k²＝，

因λ＝3 ∴k≠0 ∴k²＝>0，∴－1<m<－ 或 <m<1

容易验证k²>2m²－2成立，所以（*）成立

即所求m的取值范围为（－1，－）∪（，1）　　 ………………………14分

20．（本小题满分14分）

解：（Ⅰ）∴

当时，

，即是等比数列． ∴；　　　　 ……………………4分

（Ⅱ）由（Ⅰ）知，，若为等比数列，

 则有而

故，解得，　　………………………………7分

再将代入得成立，

所以．　　　 ………………………………………………………………8分

（III）证明：由（Ⅱ）知，所以

，　　 ………………………………………………… 9分

由得

所以，　　　 …………………… 12分

从而

．

即．　　　　　　　　　　　　　　　　 …………………………14分

21．解：（I）依题意：

在（0,+）上是增函数，

对x∈（0,+）恒成立，　　　　　　　　　…………2分

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　…………4分

　 （II）设

当t=1时，y_{m I n}=b+1；　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 …………6分

当t=2时，y_{m I n}=4+2b　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 …………8分

当的最小值为　　　　　　　　　　　　　　　　　　　　　　　　…………9分

　 （III）设点P、Q的坐标是

则点M、N的横坐标为

C₁在点M处的切线斜率为

C₂在点N处的切线斜率为　　　　 …………10分

假设C₁在点M处的切线与C₂在点N处的切线平行，则

 

……………11分

设 ……………… ①　　　　  …………12分

这与①矛盾，假设不成立.

故C₁在点M处的切线与C₂在点N处的切线不平行.　　　　　　　　　　　　　…………14分