高三理科数学第二学期期校联考

　　　　　　  　 数学(理科) 试题 　　　　　　2008.2

一、选择题：本大题共10小题，每小题5分，共50分；在每小题给出的四个选项中，有且只有一项是符合题目要求的。

1．已知复数是实数，则实数b的值为（　　 ）

　（A）　　　　  （B）　　　　　 （C）0　　　　　  （D）

2．已知集合，R是实数集，则（）∩=（　　 ）

　（A）R　　　　 （B）　　　　 （C）　　　　 （D）

3．对于直线和平面，下列命题中，真命题是(　　　 )

(A) 若，则　　　　（B）若则

(C) 若，则　　　　(D) 若，则

4．等差数列{a_n}中，S_n是其前n项和，则的值为(　　 )

　 (A) 2　　　　 (B) 1　　　　  (C) 　　　　　　(D) 3

5．曲线轴右侧的交点按横坐标从小到大依次记为P₁、P₂、P₃，…，则P₂P₄等于（　　　）(A) π　　　　　  (B) 2π　　　　　　　　　　　　  (C) 3π 　　　　　  (D) 4π

6．若点P是曲线y=x²－lnx上任意一点，则点P到直线y=x－2的最小距离为(　　)

(A)　　　　  (B)　　　　　　 (C) 2　　　　　　 (D)

7．在26枚崭新的金币中，有一枚外表与真币完全相同的假币（重量稍轻），现在只有一台天平，则在测试次数最少的一个方案中最多需要称几次就可以发现这枚假币 (　　  )

(A) 3　　　　  　　 (B) 4　　　　　  　　(C) 5　　　　　 　　 (D) 6

8．定义域为R的函数恰有5个不同的实数解等于（　　　）

（A）0　　　　　 （B）　　　　　（C）　　　　 （D）1

（第9题图）

9．如图，过抛物线的焦点F的直线l依次交抛物线及其准线于点A、B、C，若则抛物线的方程为（　　 ）

　（A）　　　 （B）　　  （C）　　　　  （D）

10．有一半径为R的圆柱（如右图），被与轴成45º角平面相截得“三角”圆柱ABC，则此“三角”圆柱的展开图为（　　 ）

二、填空题：本大题共7小题，每小题4分，共28分。

11．已知sinα=，并且a是第二象限的角，那么tanα的值等于　　　 ▲　　  。

12．圆关于直线对称，则ab的取值范围是　　 ▲　　

13．如图为类似课本研究性学习课题《杨辉三角》中的竖直平面内的一些通道，图中线条均表示通道，一钢球从入口处自上而下沿通道自由落入C处的概率是　　 ▲　　

14．同时抛掷4枚均匀的硬币3次，设4枚硬币正好出现2枚正面向上，2枚　　　反面向上的次数为ξ，则ξ的数学期望是　　 ▲　　

15．已知　　 ▲　　

16．球面上有三点A、B、C，任意两点之间的球面距离都等于球大圆周长的四分之一，且过这三点的截面圆的面积为4，则此球的体积为　　 ▲　　

17．如图，在平面斜坐标中，斜坐标定义为（其中分别为斜坐标系的x轴,y轴的单位向量），则点P的坐标为。若且动点满足,则点M在斜坐标系中的轨迹方程为　　 ▲　　

三、解答题：本大题共5小题，共72分，解答应写出文字说明，证明过程或演算步骤.

18．（本小题满分14分）

已知函数

　 （1）求函数的最小正周期；　 （2）若

19．（本题满分14分）如图，平面⊥平面，为正方形，，且分别是线段的中点。

　 （1）求证：//平面；　 （2）求异面直线与所成的角；

（第19题图）

　 （3）在线段上是否存在一点，使得点到平面的距离为.若存在，求出的值；若不存在，请说明理由。

20．（本题满分14分）如图，椭圆的左、右焦点为，过的直线与椭圆相交于、 两点。

（1） 若，且 求椭圆的离心率。

（2）若，求的最大值和最小值。

21．（本小题满分15分）、b为函数的极值点

　 （1）求证:;（2）判断函数上的单调性，并证明你的结论；

　 （3）若曲线处的切线斜率为－4，且方程有两个不等的实根，求实数的取值范围。

22．（本小题满分15分） 已知定义在R上的函数，满足条件：①对任意实数有；②对非零实数，都有

　 （1）求的值；（2）求函数的解析式；

　 （3）设函数，

　　　　、的前n项和，求证：当

答案

一．选择题：(每题5分，共50分)

题号	1	2	3	4	5	6	7	8	9	10
答案	A	C	D	B	A	A	A	C	D	D

二．填空题：(每题4分，共28分)

11._____ _ 12. ________ 13. ___ ______ 14. _ __________.

15.________.16. ___________ 17. ______

三．解答题（本大题共5小题，共72分，解答应写出文字说明，证明过程或演算步骤.）

18．（本小题满分14分）

解: （1）

　　　　　　　　　　　　　　 ………………6分

　（2）时

　………………14分

19.（本小题满分14分）

解法一：（1）证明：取AB中点H，连结GH，HE，

∵E，F，G分别是线段PA、PD、CD的中点，

∴GH//AD//EF，

∴E，F，G，H四点共面。………………1分

又H为AB中点，

∴EH//PB。…………2分

又面EFG，平面EFG，

∴PB//面EFG。…………3分

（2）解：取BC的中点M，连结GM、AM、EM，则GM//BD，

∴∠EGM（或其补角）就是异面直线EG与BD所成的角。… 4分

 在Rt△MAE中，，

同理，又，

∴在Rt△MGE中，……………………7分

故异面直线EG与BD所成的角为。……………………………………8分

（3）假设在线段CD上存在一点Q满足题设条件。过点Q作QR⊥AB于R，连结RE，则QR//AD。

∵ABCD是正方形，△PAD是直角三角形，且PA=AD=2，

∴AD⊥AB，AD⊥PA，

又，

∴AD⊥平面PAB。

又∵E，F分别是PA，PD中点，

∴EF//AD，∴EF⊥平面PAB

又面EFQ，

 ∴面EFQ⊥平面PAB。

过A作AT⊥ER于T，则AT⊥面EFQ，

∴AT就是点A到平面EFQ的距离。……………………12分

设，则，，AE=1，

在Rt△EAR中，

解得。

故存在点Q，当时，点A到平面EFQ的距离为　………………14分

解法二：建立如图所示的空间直角坐标系A－xyz，

则，，，，

，，，。

（1）证明：∵，，，……………………1分

设，即

解得。

∴，又∵与不共线，∴、与共面。……2分

∵平面EFG，∴PB//平面EFG。………………3分

（2）解：∵，，……………………4分

∴。

故异面直线EG与BD所成的角为。………………………8分

（3）假设在线段CD上存在一点Q满足题设条件。令，则，

∴点Q的坐标为，∴。

而，设平面EFQ的法向量为，则

∴。

令，则。…………………………10分

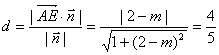又，∴点A到平面EFQ的距离………………13分

即，∴或不合题意，舍去。

故存在点Q，当时，点A到平面EFQ的距离为………………14分

20.（本小题满分14分）

解: （1），

　　　　

　　　　………………………………4分

　　　　　（2），。

　　　　 ①若垂直于轴，则，

　　　　 ，

　　　　 …………………………………………6分

②若与轴不垂直，设直线的斜率为，则直线的方程为

　　

由　　得　

，方程有两个不等的实数根。

设，.

,　 ………………………………9分

　　　　

　　　　

　　　　 =……………………………………12分

…………………………………13分

，所以当直线垂于轴时，取得最大值

当直线与轴重合时，取得最小值……………………14分　　　　　　　　　　　　　　　　　　　　　 　　　　　　　 

21.（本小题满分15分）

（1）依题设方程的两根分别为………………2分

又由题意可知：　 即……………3分

则

即……………5分

（2）由（1）：

 

 （3）由，

　　的变化情况如下：

	(－∞,－3)	－3			－1	（－1，0）	0
	—	0	+	+	0	—
		极小值			极大值 －1

　 又 ………………13分

　　　………………15分

22. （本小题满分15分）

解：（1）由题意：

　　　　又　……………2分

（2）当

　　故两式联立可得，

　　　………………5分

　 （3）由（I）可得，

　　联立，

　　所以 ………………9分

　　

　　

　　　　　　　　　　　　　　　　 ………………15分