04届高三第五次模拟数学试卷
命题人:曹升阳
时间:04年5月10日
一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
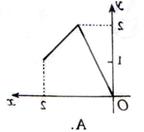
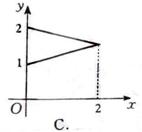
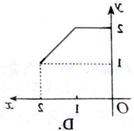
1.设集合![]() ,在图中能表示从集合
,在图中能表示从集合![]() 到集合
到集合![]() 的映射的是(
)
的映射的是(
)

2. 设![]() 是方程
是方程![]() 的两个不等实根,那么过点
的两个不等实根,那么过点![]() 的直线方程为(
)
的直线方程为(
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.已知函数![]() 满足
满足![]() 则
则![]() 的最小值为(
)
的最小值为(
)
A. ![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
4. 已知命题![]() :函数
:函数![]() 的值域为
的值域为![]() ,命题
,命题![]() :函数
:函数![]() 是减函数,若
是减函数,若![]() 或
或![]() 为真命题,
为真命题,![]() 且
且![]() 为假命题,则实数
为假命题,则实数![]() 的取值范围是(
)
的取值范围是(
)
A.![]() B.
B.![]() <2 C.1<
<2 C.1<![]() <2
<2 ![]() D.
D.![]() 或
或![]()
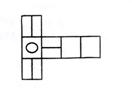
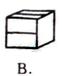
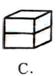
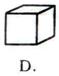
5. 下图代表未折叠正方体的展开图,将其折叠起来,变成正方体后,图形是( )

7. 电流强度![]() (安培)随时间
(安培)随时间![]() 变化的函数
变化的函数![]() 的图像如图所示,则当
的图像如图所示,则当![]() (秒)时的电流强度是 ( )
(秒)时的电流强度是 ( )
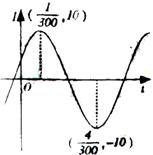
A. 0安培 B. 10安培
C. -10安培 D. 5安培
8. ![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9. 已知![]() ,则
,则![]() 的值( )
的值( )
A. -4 B. 0 C. 8 D. 不存在
12. 定义一种运算![]() ,对自然数n满足以下运算性质:(1)
,对自然数n满足以下运算性质:(1)![]() ;(2)
;(2)![]() ,则
,则![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
二、填空题:(本大题共4小题,每小题4分,共16分.)
13.已知正态总体落在区间(![]() )里的概率是
)里的概率是![]() ,那么相应的正态曲线
,那么相应的正态曲线![]() 在
在![]() =________时,达到最高点.
=________时,达到最高点.
14.已知函数![]() 且
且![]() ,则
,则![]() 从小到大顺序为_____________.
从小到大顺序为_____________.
16.![]() 中,A、B、C为三个内角,
中,A、B、C为三个内角,![]() 、
、![]() 、
、![]() 分别为它的对边,给出命题中:
分别为它的对边,给出命题中:
(1)![]() ,则
,则![]() 为等腰或直角三角形.(2)
为等腰或直角三角形.(2)![]() <0,则
<0,则![]() 钝角三角形.(3)
钝角三角形.(3)![]() ,
,
则![]() 为直角三角形.(4)
为直角三角形.(4)![]() <0,则
<0,则![]() 为钝角三角形.正确命题为__________(写出所有正确命题标号).
为钝角三角形.正确命题为__________(写出所有正确命题标号).
三、解答题:(本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.)
17.(本小题满分12分)
在一次环保知识竞赛中,有6道选择题和2道判断题放在一起供抽取,每支代表队要抽3次,每次只抽一道题回答.
(1) 不放回的抽取试题,求只在第三次抽到判断题的概率;
(2) 有放回的抽取试题,求在三次抽取中抽到判断题的个数![]() 的概率分布及
的概率分布及![]() 的期望.
的期望.
18.(本小题满分12分)
已知函数![]()
(1) 若![]() 在
在![]() 上是增函数,求
上是增函数,求![]() 的取值范围;
的取值范围;
(2)
求![]() 在区间
在区间![]() 上的最大值.
上的最大值.
19. (本小题满分12分)
如右图所示,点![]() 分别是正方体
分别是正方体![]() 上的点.
上的点.
(1)
 若
若![]() ,求证:无论点P在
,求证:无论点P在![]() 上如何移动总有
上如何移动总有![]() 丄
丄![]() ;
;
(2)
若![]() 且
且![]() 丄平面
丄平面![]() ,求二面角
,求二面角![]() 的大小;
的大小;
(3)
棱![]() 上是否存在这样的点P,使得平面
上是否存在这样的点P,使得平面![]() 丄平面
丄平面![]() ?证明你的结论.
?证明你的结论.
20. (本小题满分12分)
设一次函数![]() 的图像关于直线
的图像关于直线![]() 对称的图象为C,且
对称的图象为C,且![]() ,若点
,若点![]()
![]() 在曲线C上,并有
在曲线C上,并有![]()
(1) 求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求
,求![]() 的值.
的值.
 21.(本小题满分12分)
21.(本小题满分12分)
如图所示,平地上有一条水沟,沟沿是两条长100![]() 的平行线段,沟宽
的平行线段,沟宽![]() 为2
为2![]() ,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为
,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为![]() ,对称轴与地面垂直,沟深
,对称轴与地面垂直,沟深![]() ,沟中水深1
,沟中水深1![]() .
.
(1) 求水面宽.
(2) 现要把这条水沟改挖(不准填土)成截面为等腰梯形的沟,使沟的底面与地面平行,问改挖后的沟底宽为多少米时,所挖的土最少?
22.(本小题满分14分)
已知在平面直角坐标系![]() 中,向量
中,向量![]() ,
,![]() 的面积为
的面积为![]() ,且
,且![]() ,
,![]() .
.![]()
(1) 设4<![]() <
<![]() ,求向量
,求向量![]() 与
与![]() 的夹角
的夹角![]() 的取值范围;
的取值范围;
(2)设以原点![]() 为中心,对称轴在坐标轴上,以
为中心,对称轴在坐标轴上,以![]() 为右焦点的椭圆经过点M,且
为右焦点的椭圆经过点M,且![]() ,
,![]() ,当
,当![]() 取最小值时,求椭圆的方程.
取最小值时,求椭圆的方程.
数学试卷参考答案
一、选择题:DDCDB AAACB DB
二、填空题:13. ![]() ; 14.
; 14. ![]() ; 15.
; 15. ![]() ; 16.(1)(2)
; 16.(1)(2)
三、解答题:
17、(1)若不放回抽取三道试题有![]() 种方法,只在第三次抽到判断题有
种方法,只在第三次抽到判断题有![]() 种方法。
种方法。
则只在第三次抽到判断题的概率![]() .
.
(2)若有放回的抽取试题,每次抽取到的判断题概率为![]() ,且相互独立。所以在三次抽取中抽到判断题的个数
,且相互独立。所以在三次抽取中抽到判断题的个数![]() 的概率分布为:
的概率分布为:
![]()
![]()
![]()
![]()
|
| 0 | 1 | 2 | 3 |
|
|
|
|
|
|
![]() ~
~![]()
18.(1)![]() .
.![]()
![]()
(2)当![]() 时,
时,![]()
![]() ;当
;当![]() 时,方程
时,方程![]()
当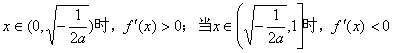 .
.
![]() .
.
19、(1)证![]() 丄平面
丄平面![]() ;(2)所求角的大小为
;(2)所求角的大小为![]() ;(3)存在点P,且P为
;(3)存在点P,且P为![]() 的中点,使得平面
的中点,使得平面![]() 丄平面
丄平面![]() ,先证明
,先证明![]() 丄平面
丄平面![]() ,再取
,再取![]() 中点E,连结
中点E,连结![]() ,有
,有![]() ∥
∥![]() ,从而
,从而![]() 丄平面
丄平面![]() ,故结论成立.
,故结论成立.
20.(1)设![]() .
.
由![]()
![]() . ①
. ①
![]() ,在曲线
,在曲线![]() 上,
上,
![]()
![]() ②
②
由①②得![]() 故曲线
故曲线![]() 的方程为
的方程为![]()
由点![]() .于是
.于是
![]() .即
.即![]()
![]()
(2)![]()
![]()
![]()
![]()
![]()
![]()
21.(1)建立直角坐标系,设抛物线的方程为![]()
![]() .于是抛物线的方程为
.于是抛物线的方程为![]() .
.![]() .
.
(2)设![]()
![]()
![]() ,
,
即![]() .于是,
.于是,![]()
![]()
![]()
令![]() .
.
![]() S最小,此时所挖土最少,这时
S最小,此时所挖土最少,这时![]() 因此,当
因此,当![]() 时,所挖土最少。
时,所挖土最少。
22、
(1)由![]() ,由
,由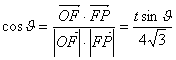 ,得
,得![]() .
.
![]() 4<
4<![]() <
<![]()
![]()
![]()
![]() 夹角
夹角![]() 的取值范围是
的取值范围是![]() .
.
(2)设![]()
![]()
![]()
![]()
![]()
![]()
![]() 又由
又由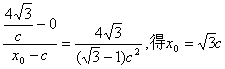
![]()
![]()
![]()
椭圆长轴![]()
![]()
故所求椭圆方程为![]() .
.