北京市西城区2001年抽样测试高三数学试卷(文科)
学校____________ 班级____________ 姓名____________
| 题号 | 一 | 二 | 三 | 总分 | |||||
| (17) | (18) | (19) | (20) | (21) | (22) | ||||
| 分数 | |||||||||
参考公式:三角函数的积化和差公式 正棱台、圆台的侧面积公式
![]()
![]()
![]() 其中
其中![]() 、
、![]() 分别表示上、下底面周长,
分别表示上、下底面周长,![]()
![]() 表示斜高或母线长
表示斜高或母线长
![]()
![]()
其中![]() 、
、![]() 分别表示上、下底面积,
分别表示上、下底面积,![]() 表示高
表示高
一、选择题:本大题共12小题;每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合要求的。每小题选出答案后,用铅笔在下表中将对应答案标号涂黑。
`
| 题号 | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) |
| 答 案 | A B C D | A B C D | A B C D | A B C D | A B C D | A B C D | A B C D | A B C D | A B C D | A B C D | A B C D | A B C D |
1.已知集合![]() ,若M∩N≠
,若M∩N≠![]() ,则
,则![]() 等于()。
等于()。
(A)1 (B)2 (C)1或2 (D)8
2.从4台A型笔记本电脑和5台B型笔记本电脑中任意选取3台,其中至少要有A型和B型笔记本电脑各一台,则不同的选取方法共有( )。
(A)140种 (B)84种 (C)70种 (D)35种
3.复数![]() 满足
满足![]() ,则
,则![]() 的最小值是( )。
的最小值是( )。
(A)1 (B)2 (C)![]() (D)
(D)![]()
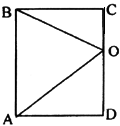
4.设O是矩形ABCD的边CD上一点,以直线CD为轴旋转这个矩形所得的圆柱体的体积为V,其中以OA为母线的圆锥的体积为![]() ,则以OB为母线的圆锥的体积等于( )。
,则以OB为母线的圆锥的体积等于( )。
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5.将曲线C向右平移3个单位,再向下平移1个单位得到曲线![]() ,若曲线
,若曲线![]() 的方程为
的方程为![]() ,则曲线C的焦点坐标为( )。
,则曲线C的焦点坐标为( )。
(A)(6,–1),(0,–1) (B)(–6,1),(0,1)
(C)(–3,2),(–3,–4) (D)(3,2),(3,–4)
6.已知![]() 且
且![]() ,则下列不等式成立的是( )。
,则下列不等式成立的是( )。
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
7.若圆![]() 上恰有相异两点到直线
上恰有相异两点到直线![]() 的距离等于1,则r的取值范围是( )。
的距离等于1,则r的取值范围是( )。
(A)[4,6] (B)![]() (C)
(C)![]() (D)(4,6)
(D)(4,6)
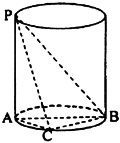
8.如图,PA 为圆柱的母线,AB为底面圆的直径,C为下底面圆周上一点,![]() ,则( )。
,则( )。
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
9.为了使函数![]() 在区间[0,1]上至少出现50次最大值,则
在区间[0,1]上至少出现50次最大值,则![]() 的最小值是( )。
的最小值是( )。
(A)98![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
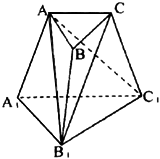
10.如图,三棱台![]() 中,已知
中,已知![]() ,高为
,高为![]() ,则四面体
,则四面体![]() 的体积为( )。
的体积为( )。
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
11.在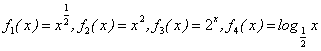 四个函数中,当
四个函数中,当![]() 时,使
时,使![]() 成立的函数是( )。
成立的函数是( )。
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
12.已知双曲线![]() 和椭圆
和椭圆![]() 的离心率互为倒数,那么以a,b,m为边长的三角形是( )
的离心率互为倒数,那么以a,b,m为边长的三角形是( )
(A)锐角三角形 (B)直角三角形 (C)钝角三角形 (D)锐角或钝角三角形
二、填空题:本大题共4小题,每小题4分。共16分,把答案填在题中横线上。
13.数列![]() 满足
满足![]() ,则数列
,则数列![]() 的通项公式
的通项公式![]() =_________。
=_________。
14.设![]() 是椭圆
是椭圆![]() 的两个焦点,P是椭圆上一点,且
的两个焦点,P是椭圆上一点,且![]() ,则
,则![]() =_________。
=_________。
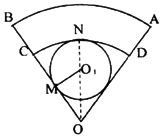
15.一扇形铁皮AOB,半径OA=72cm,圆心角![]() ,现剪下一个扇环ABCD做圆台形容器的侧面,并从剩下的扇形OCD内剪下一个最大的圆刚好做容器的下底(圆台的下底面大于上底面)(如图),则OC的长为______________。
,现剪下一个扇环ABCD做圆台形容器的侧面,并从剩下的扇形OCD内剪下一个最大的圆刚好做容器的下底(圆台的下底面大于上底面)(如图),则OC的长为______________。
16.设函数![]()
给出以下四个论断:
①它的图象关于直线![]() 对称;
对称;
②它的图象关于点(![]() )对称;
)对称;
③它的周期是![]() ;
;
④在区间![]() 上是增函数
上是增函数
以其中两个论断作为条件,余下论断作为结论,写出你认为正确的两个命题:
(1)________________________________________;
(2)________________________________________。
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤。
17.(本题满分12分)
解不等式![]() 。
。
18.(本题满分12分)
在![]() 中,已知角
中,已知角![]() 的对应边分别为
的对应边分别为![]() ,且
,且![]() 成等差数列。
成等差数列。
(1)求证:![]() ;
;
(2)求![]() 的值。
的值。
19.(本题满分12分)
如图,![]() 平面ABCD,四边形ABCD是矩形,PA=AD=a,M,N分别是AB,PC的中点,
平面ABCD,四边形ABCD是矩形,PA=AD=a,M,N分别是AB,PC的中点,
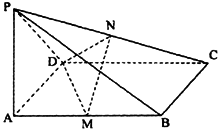
(1)求平面PCD与平面ABCD所成二面角的大小;
(2)求证:![]() 平面PCD;
平面PCD;
(3)当AB的长度变化时,求异面直线PC与AD所成角的可能范围。
20.(本题满分13分)
已知双曲线![]() 和椭圆
和椭圆![]() :
:![]() 有公共的焦点,它们的离心率分别是
有公共的焦点,它们的离心率分别是![]() 和
和![]() ,且
,且![]()
(1)求双曲线![]() 的方程;
的方程;
(2)圆D经过双曲线![]() 的两焦点,且与x轴有两个交点,这两个交点间的距离等于8,求圆D的方程。
的两焦点,且与x轴有两个交点,这两个交点间的距离等于8,求圆D的方程。
21.(本题满分12分)
市场营销人员对过去几年某商品的价格及销售数量的关系作数据分析发现有如下规律:该商品的价格每上涨x%(x>0),销售数量就减少kx%(其中k为正常数)。目前,该商品定价为a元,统计其销售数量为b个。
(1) 当![]() 时,该商品的价格上涨多少,就能使销售的总金额达到最大?
时,该商品的价格上涨多少,就能使销售的总金额达到最大?
(2) 在适当的涨价过程中,求使销售总额不断增加时k的取值范围。
22.(本题满分13分)
![]() 都是各项为正的数列,对任意的自然数
都是各项为正的数列,对任意的自然数![]() ,都有
,都有![]() 成等差数列
成等差数列![]() ,
,![]() 成等比数列。
成等比数列。
(Ⅰ)求证:![]() 是等差数列;
是等差数列;
(Ⅱ)如果![]() ,求
,求![]() 。
。
