61．棱柱、棱锥、棱台（2）

一、典型例题

1．  在一张硬纸上挖去一个半径为的圆洞，然后把此洞套在一个底面边长为4，高为6的正三棱锥上，并使纸面与锥底面平行，则能穿过这张纸面的棱锥的高的最大值是多少？[9/2]

2．  在三棱台A₁B₁C₁－ABC中，侧棱B₁B⊥底面ABC，∠ABC＝∠AA₁C＝90°，①求证：AA₁⊥A₁B₁；②若A₁B₁＝B₁C₁＝1，AB＝2，求该棱台的侧面积。[3+]

3．  如图，斜三棱柱ABC－A₁B₁C₁的底面是边长为2的正三角形，顶点A₁在底面ABC上射影O是⊿ABC的中心，AA₁与AB的夹角是45°，①求证：AA₁⊥平面A₁BC；②求此棱柱的侧面积。[4+2]

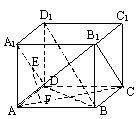
4．  如图，正方体ABCD－A₁B₁C₁D₁中，EF是异面直线AC和A₁D的公垂线，求EF和BD₁的关系。[∥]

5．  直平行六面体的底面是菱形，过不相邻的两对侧棱的截面的面积是Q₁和Q₂，求它的侧面积。[2]

6．  在三棱柱ABC－A₁B₁C₁中，AB＝，BC＝CA＝AA₁＝a，A₁底面ABC上的射影O在AC上，①求AB与侧面AC₁所成的角；②若O恰为AC的中点，求此三棱柱的侧面积。[45°、]

7．  正四棱锥侧棱和底面所成的角为a，相邻两侧面所成的二面角为b，求证：cosb=。