60．棱柱、棱锥、棱台（1）

一、典型例题

1．  已知正三棱柱的高为3 cm，一个侧面三角形的面积为 cm²，求这个正三棱锥的侧面和底面所成的二面角的大小。[60°]

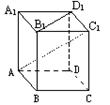
2．  如图，四棱柱ABCD－A₁B₁C₁D₁中给出三个论断：①四棱柱ABCD－A₁B₁C₁D₁是直四棱柱；②底面ABCD是菱形；③AC₁⊥B₁D₁，以其中两个论断作条件，余下一个作为结论，可以得到三个命题，其中有几个真命题？为什么？

3．  已知三棱台ABC－A₁B₁C₁的侧面A₁ACC₁是底角为45°的等腰梯形，且该侧面与底面垂直，∠ACB＝90°，①求证：二面角A－BB₁－C为直二面角；②若AB＝5，BC＝3，求二面角A₁－AB－C的大小。[arctg]

4．  在长方体中，AB＝BC＝a,=b,(b>a)，连结，过作交于E，①求证：⊥平面；②求三棱锥的体积。[a⁴/6b]

5．  已知三棱锥各侧面与底面成60°角，底面三角形各角成等差数列，且最大边与最小边是方程3x²-21x+13=0的两根，求此三棱锥的侧面积和体积。[]

6．  正三棱锥S－ABC的底面边长是2a，E、F、G、H分别是SA、SB、BC、CA的中点，求EFGH面积的取值范围。[()]

7．　 已知直四棱柱ABCD－A₁B₁C₁D₁的底面ABCD是矩形，又AA₁＝AB，E、F分别是BD₁和AD的中点，①求异面直线EF和CD₁所成的角；②证明：EF是异面直线的公垂线；③又若G是B₁C₁的中点，求证：平面A₁FCG⊥平面BCD₁。[90°]