蕲春一中高三(9)测试题四

一、　　　　　　 选择题：1. 设sin(α＋β)＝，sin(α－β)＝，则log(tgαctgβ)=

 A．- 2　　　　B.2　　　　　　　  C. 　　　　　　　　  D.-

2. 四棱锥P-ABCD的底面ABCD是一个正方形， PD是垂直于底面ABCD，则这个四棱锥的五个面中互相垂直的平面共有

A.3对　　　　B.4对　　　　　　　 C.5对　　　　　　　  D.6对

3. 已知圆的方程为(x- 3)²+y²= 4 和直线y=mx的交点分别为P、Q，O为原点，则OP·OQ的值等于

　 A．　　　　B.1+m²　　　　　　　  C.5　　　　　　　　  D.10

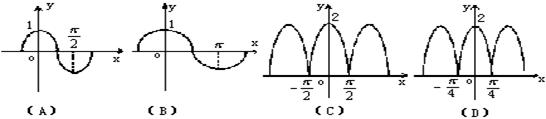
4. 设复数z＝cosx＋isinx，那么函数f(x)＝z³＋的图象是

5. 一个正三棱锥与一个正四棱锥，他们的所有棱长都相等，把这个正三棱锥的一个侧面重合在正四棱锥的一个侧面上，这个组合体可能是

A.正五棱锥　　　B.斜三棱柱　　　　 C.正三棱台　 　　　 D.正三棱柱

6. 圆锥的毋线长为1cm，侧面展开图的圆心角为，该圆锥的体积为

（A）πcm³　　 （B）πcm³　　 （c）πcm³　　 （D）πcm³

7. 函数y=f（x）有反函数y=f^-－1（x）把y=f（x）的图象在直角坐标平面内绕原点顺时针方向转动90⁰后得到另一个函数的图象，这另一个函数是

（A）y=f^－1（－x）　 （B）y=f^－1（x）　 （C）y=－f^－1（－x）　　（D）y=－f^－1（x）

8. 台体（棱台或圆台）中一个平行于底面的截面把台体分成上、下两部分，如果台体的上底面积、截面面积、下底面积的比为1:4:9，则截面把该台体分成的上、下两部分的体积之比为

（A）8:27　　　　（B）7:19　　　 （C）5:12　　  （D）3:5

9. 过点M（－2， 0）的直线 l与椭圆 x²+2y²=2交于 P_1， P₂两点，线段 P₁P₂的中点为 P，设直线 l的斜率为 k₁（ k₁0），直线 OP的钭率为k ₂，则 k₁k₂的值等于

（ A） 2　　　（ B） －2 　　 （ C） 　　　　 （ D）－ 翰林汇

10. 在三棱柱ABC－A₁B₁C₁的侧棱A₁A和B₁B上各有一动点P、Q，满足A₁P=QB，过P、Q、C三点的截面把棱柱分成两部份，则上、下部份的体积之比为（　　）。

A、3 ：1　　 B、2 ：1　　  C、4 ：1　　　 D、：1

11. 计算机是将信息转换成二进制数进行处理的，二进制即“逢二进一”，如（1101）₂表示二进制数，将它转换成十进制数的形式是1×3³+1×2²+0×2¹+1×2⁰=13， 转换成十进制数的形式是（　　）。

A、　　B、　　 C、　　　 D、

12. 已知直线l₁：y=xsinα和直线l₂：y=2x+c，则直线l₁与l₂

　　　 A．通过平移可以重合 　　  　　　　 B．不可能垂直

　　　 C．可能与x轴围成等腰直角三角形　　 D．通过绕l₁某一点旋转可以重合

一大题答题卡：

题号	1	2	3	4	5		6	7	8	9	10		11	12
答案

二、填空题：13. 直线y- kx- 1=0与椭圆 + = 1恒有公共点，则m的取值范围为　　

14. 已知数列{a_n}满足条件a₁=2，a_n+1= a_n+4n+2(n∈N)，则数列{ a_n }的通项公式为　　 　　 

15. 如图，有一座六角亭，相邻两根柱子之间的距离为1.6米，柱高2.7米，不算葫芦顶，亭顶最高处高3.9米，则亭顶相邻两面的所成二面角为　　　　　　　　　　　　　   

16. 已知x、y为正实数，且x，a₁，a₂，y成等差数列，x，b₁，b₂，y成等比数列，则的取值范围是　　　　　　　　　　　　　  .

三、解答题： 17. 复数z₁和z₂满足z₁+ z₂=i， z₁· z₂=1，设u=，若argu=θ，求cosθ的取值范围。

18. 在四棱柱ABCD—A₁B₁C₁D₁中，ABCD为菱形，AB=2，AA₁=1，∠A₁AD=∠A₁AB=∠DAB=60⁰.（1）求直线AA₁与平面B₁CD₁所成角的大小；（2）求二面角C₁—B₁D₁--C的大小；（3）求四棱柱ABCD—A₁B₁C₁D₁的体积。

19. 设抛物线y=2px (p>0)上有两动点A、B，F为焦点，且AF+BF=8，又线段AB的垂直平分线恒过定点Q(6，0).　 （1）求抛物线方程；　 （2）求△AQB面积的最大值。

20. 某企业在“减员增效” 中，对部分人员实行分流。规定分流人员第一年可以在原单位领取工资100%，从第二年起，以后每年都能在原单位按上一年的 领取工资。该企业根据分流人员的技术特长，计划创办新的经济实体，该实体预计第一年属投资阶段，员工没有收入，第二年每人可获b元收入，从第三年起每人每年的收入可在上一年基础上递增50%。如果某人分流前工资收入每年a元，求：（1）分流到新的经济实体后第n年的总收入；（2）当b= a时，这个人哪一年的收入最少？最少收入是多少？

21. 设f（x）是定义域在（－，0）∪（0，+）的奇函数，且在（0，+）上是增函数.

（1）判断f（x）在（－，0）上的单调性，并用单调函数的定义加以证明；（2）若f（1）=0，解关于x的不等式f[log_a（1—x²）+1]>0，其中a>1；（3）若m>0，n>0时f（mn）=f（m）+f（n），且f（－2）=－1. 求logf（t）+1>0时t的取值范围。

22. 已知函数f(x)在（－1，1）上有定义，f()= - 1且满足x、y∈（- 1，1） 有f(x) + f(y) = f() ．

（1）证明：f(x)在（- 1，1）上为奇函数；（2）对数列x₁=，x_n+1= ，求f(x_n)；（3）比较++…+与- 的大小.