高三年级第一学期期中考试数学试题(1)
一、选择题(每题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1.已知集合![]() ,
,![]() 要使
要使![]() ,则
,则![]() 满足的条件是
满足的条件是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.设![]() ,
,![]() ,给出下列四个图象,其中能表示从集合
,给出下列四个图象,其中能表示从集合![]() 到集合
到集合![]() 的函数关系的有
的函数关系的有
A.0个 B.1个 C.2个 D.3个
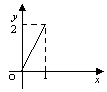

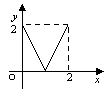

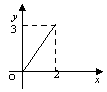

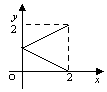

3.函数![]()
![]() 的最小正周期为1,则
的最小正周期为1,则
A.![]() ,
,![]() 在
在![]() 上是增函数,
上是增函数, ![]() 为偶函数
为偶函数
B.![]() ,
,![]() 在
在![]() 上是减函数,
上是减函数,![]() 为偶函数
为偶函数
C. ![]() ,
,![]() 在
在![]() 上是减函数,
上是减函数,![]() 为奇函数
为奇函数
D.![]() ,
,![]() 在
在![]() 上是增函数,
上是增函数,![]() 为奇函数
为奇函数
4.若函数![]() 的定义域是
的定义域是![]() ,则函数
,则函数![]() 的定义域是
的定义域是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.在区间![]() 上为减函数的是
上为减函数的是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知![]() ,且
,且![]() ,则
,则![]() 的值
的值
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() 的大小关系为
的大小关系为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.把一个函数的图象按![]() 平移后得到的图象解析式为
平移后得到的图象解析式为![]() ,那么原来的函数解析式为
,那么原来的函数解析式为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.已知![]() 是互相垂直的单位向量
是互相垂直的单位向量![]() ,
,![]() ,若
,若![]() ,
,![]() 的夹角为锐角,则
的夹角为锐角,则![]() 的范围是
的范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.某城市加强环境保护,绿地面积每年都比上一年增长![]() ,经过
,经过![]() 年后,绿地面积可以增长为原来的
年后,绿地面积可以增长为原来的![]() 倍,则函数
倍,则函数![]() 的图象大致是
的图象大致是
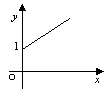

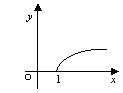

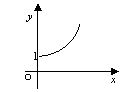

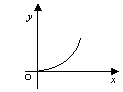

A B C D
11.公差不为零的等差数列的第二,第三,第七项恰好构成等比数列,则它的公比为
A.![]() B.
B.![]() C.
C.![]() D.4
D.4
12.已知数列![]() 的通项公式
的通项公式![]()
![]() ,则数列
,则数列![]() 前30项的最大项和最小项分别是
前30项的最大项和最小项分别是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
13.函数![]() 的定义域是
的定义域是
14.等差数列![]() 中,
中,![]() ,则
,则![]()
15.如果不等式![]() 有解,则实数
有解,则实数![]() 的取值范围是
的取值范围是
16.已知定义域为![]() 的函数
的函数![]() 满足当
满足当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,则
,则![]() 的值等于
的值等于
三、解答题(共74分)
17.(本小题12分)在![]() 中,已知
中,已知![]() ,
,![]() ,求
,求![]()
18.求证:![]()
(本小题12分)
19.(本小题12分)已知![]() ,
,![]() ,
,![]()
(1)求![]() 与
与![]() 的夹角;
的夹角;
(2)求![]() 与
与![]() ;
;
(3)若![]() ,
,![]() ,作
,作![]() ,求
,求![]()
20.(本小题12分)已知数列![]() 中,前
中,前![]() 项和
项和![]() ,数列
,数列![]() 中
中![]() ,
,![]() ,且存在常数
,且存在常数![]() ,使得对一切正整数
,使得对一切正整数![]() ,
,![]() 恒为常数
恒为常数![]() ,试求出
,试求出![]() 和
和![]() 之值
之值
21.(本小题12分)已知函数![]() ,
,![]() 是奇函数当
是奇函数当![]() 时,
时,![]() 有最小为2,设当点
有最小为2,设当点![]() 是函数图象上的点时,点
是函数图象上的点时,点![]() 是函数
是函数![]() 图象上的点
图象上的点
(1)求证:![]()
(2)求函数![]() 的表达式
的表达式
22.已知定义在![]() 上的函数
上的函数![]() ,对任意的
,对任意的![]() ,恒有
,恒有![]() 成立
成立
(1)求![]() 的值;
的值;
(2)求证:当![]() 时,
时,![]()
(3)若![]() 时,恒有
时,恒有![]() ,试判断
,试判断![]() 在
在![]() 上的单调性并说明理由。
上的单调性并说明理由。
(本小题14分)
参考答案
一、选择题(每题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | B | B | B | C | B | A | B | A | C | D | C |
二、填空题(每小题4分,共16分)
13、![]() 14、105
15、
14、105
15、![]()
16、48
三、解答题(共74分)
17、解:![]() ,
,![]() …………3分
…………3分
当![]() 时,
时,![]()
由![]()
可以得出![]() ,又
,又![]()
得出![]() ,由此可知
,由此可知![]() ,矛盾
…………8分
,矛盾
…………8分
故必有![]()
![]() ,
,
![]() ………12分
………12分
18、解:![]()
![]() ……4分
……4分
![]() ……6分
……6分
![]() 在
在![]() 上为减函数
上为减函数
![]()
……9分
![]()
……11分
当且仅当![]() 时取等号
……12分
时取等号
……12分
19、解:(1)![]()
![]() ……1分
……1分
![]() ,
,![]()
![]()
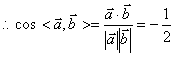 ……3分
……3分
![]()
![]() 与
与![]() 的夹角为
的夹角为![]() ……4分
……4分
(2)![]()
![]() ……6分
……6分
![]()
![]() ……8分
……8分
(3)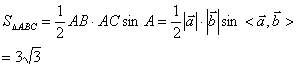 ……12分
……12分
20、解:当![]() 时,
时, ![]()
![]() ……2分
……2分
当![]() 时,
时, ![]()
![]()
![]()
![]() ……4分
……4分
![]() 存在常数
存在常数![]() ,使得对一切正整数
,使得对一切正整数![]() ,
,![]() 恒为常数
恒为常数![]()
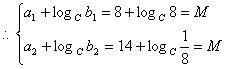 ……9分
……9分
![]() ……12分
……12分
21、解:![]() 为奇函数
为奇函数
![]()
即![]()
![]() ……3分
……3分
![]()
![]()
![]()
又![]() 有最小值为2
有最小值为2
![]()
![]() ……6分
……6分
(2)![]() 在
在![]() 图象上时,点
图象上时,点![]() 在
在![]() 图象上
图象上
![]() 设
设![]() 在
在![]() 图象上,则
图象上,则![]() 在
在![]() 图象上
图象上
![]() ……10分
……10分
![]()
![]() ……12分
……12分
22、解:(1)![]()
![]() ……3分
……3分
(2)![]()
![]() ……6分
……6分
(3)![]() 在
在![]() 上为减函数
上为减函数
设![]() ,则
,则![]() ……7分
……7分
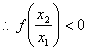 ……8分
……8分
又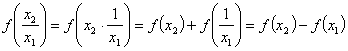
……11分
![]()
![]() ……12分
……12分
![]() 在
在![]() 上为减函数 ……14分
上为减函数 ……14分