数学文科:模拟试卷二
一、选择题
1. 已知复数z=(m![]() -m-2)+(m
-m-2)+(m![]() -3m+2)i,对应点z位于复平面的虚轴上,
-3m+2)i,对应点z位于复平面的虚轴上,
则实数m等于( )
(A) 1 (B)-1
(C) 2 (D)-1和2
2. 已知N={x|x≤5},![]() ,则下列关系中正确的是( )
,则下列关系中正确的是( )
(A) a包含于N (B) a不属于N
(C) {a}∈N (D) {a}真包含于N
3. 若函数
f(x)=log2x+3 (x≥1) ,则![]() 为( )
为( )
(A) ![]() (x∈R)
(B)
(x∈R)
(B)![]() (x∈[3,+∞))
(x∈[3,+∞))
(C) ![]() (x∈R)
(D)
(x∈R)
(D) ![]() (x∈[3,+∞))
(x∈[3,+∞))
4. 直线 ![]() 在 y 轴上的截距是( )
在 y 轴上的截距是( )
(A) |b| (B) ±b
(C) b![]() (D) -b
(D) -b![]()
5. 公比是 ![]() 的数列是( )
的数列是( )
(A)递增数列 (B)递减数列
(C)摆动数列 (D)以上结论都不对
6. 已知a、b、c、d∈R,且a>b,c>d,下列不等式中一定成立的是( )
(A)a-c>b-d
(B)![]() >
>![]()
(C)ac>bd (D)a+c-b-d>0
7. 函数 y=sinx-2cosx 的最小正周期是( )
(A) 2π
(B) ![]()
(C) π
(D) ![]()
8. sin20°cos70°+cos80°cos40°的值是( )
(A)![]() (B)
(B) ![]() (C)
(C)![]() (D)
(D)![]()
9. 下列四个命题
(1) 若直线m∥平面α,平面α⊥平面β,则m⊥β。
(2) 若平面α⊥平面β,平面β⊥平面γ,则α⊥γ。
(3) 若平面m⊥平面α,平面α⊥平面β,则m∥β。
(4) 若平面α∥平面β,直线m在平面α内,则m∥β。
其中正确命题的个数是( )
(A) 1个 (B) 2个
(C) 3个 (D) 4个
10. 从6个男同学和4个女同学中选出3人参加数学竞赛,其中男生甲必须参加,
且选出3人中至少有一个女同学,共有选法的种数有( )
(A) ![]() (B)
(B)![]() ·
·![]()
(C) ![]() (D)
(D)
![]() ·
·![]() ·
·![]()
11. 如果函数
y=sin2x+acos2x 的图象关于直线 ![]() 对称,则a等于( )
对称,则a等于( )
(A) ![]() (B)
(B)
![]() (C) 1
(D) -1
(C) 1
(D) -1
12. 抛物线 ![]() 的焦点坐标是( )
的焦点坐标是( )
(A)![]() (B)(0,
(B)(0,![]() )
)
(C)(![]() ,0)
(D)(0,
,0)
(D)(0,![]() )
)
13. (a+b+c+d+e)![]() 的展开式中,ab
的展开式中,ab![]() c的系数是( )
c的系数是( )
(A) 10 (B) 20
(C) 24 (D) 28
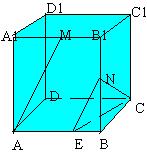
14. 在棱长为1的正方体 ABCD-A1B1C1D1 中,M和N分别为A1B1 和BB1 的中点,
则直线AM和CN所成角的余弦是( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
15. 要制造一个底面半径为4cm,母线长为6cm的圆锥,用一块长方形铁皮剪出它的侧面,
这样的长方形铁皮的最小长、宽尺寸为( )
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
二、填空题
16. 数列 ![]() (n=1,2,3…) 的各项和为 ( )。
(n=1,2,3…) 的各项和为 ( )。
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
[解答]
17. 已知圆柱轴截面周长为 1,则圆柱的体积 V 的最大值为( )。
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
[解答]
18. 已知tgx=-2,则
![]() 的值为( )
的值为( )
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
[解答]
19. 中心在原点,准线方程为y=±4,离心率为 ![]() 的椭圆方程为( )。
的椭圆方程为( )。
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
[解答]
三、解答题
20. 求函数![]() 的最小值。( )
的最小值。( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
[解答]
21. 满足![]() 实数,且z+3的辐角主值是
实数,且z+3的辐角主值是 ![]() 的虚数z是否存在?
的虚数z是否存在?
若存在,求出虚数z;若不存在,请说明理由。
[解答]
|
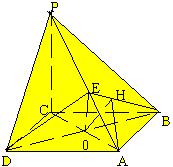
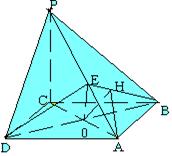
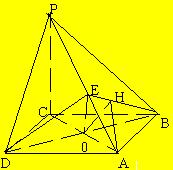
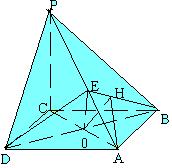
22. 如右图:四棱锥P—ABCD的底面是边长为a的菱形, ∠ABC等于60°, PC⊥平面AC,PC=a,E是PA中点。 |
(1) 求证:平面EDB⊥平面AC。
[解答]
(2) 求点E到平面PBC的距离( $S*C$ )。
|
(A) (C) |
[解答]
(3) 求二面角A—EB—D的正切值。( $S*D$ )
|
(A) (C) |
[解答]
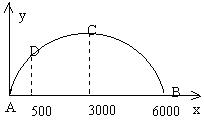
23. 炮弹的运行轨道若不计空气阻力是抛物线,现测得我炮位A与目标B的水平距离为
6000m,而当射程是6000m时,炮弹的运行轨道的最大高度是1200m,在A、B间距离
A点500m处有一高达350m的障碍物,试计算炮弹能否越过障碍物。
[解答]
24. 已知数列 {an} 中,Sn 是它的前 n 项和,并且Sn+1=4an+2 (n=1, 2,…),a1=1
(1) 设bn=an+1-2an。 (n=1,2,…)。求证数列 {bn} 是等比数列;
[解答]
(2) 设 ![]() (n=1,2,…) 求证数列 {cn} 是等差数列;
(n=1,2,…) 求证数列 {cn} 是等差数列;
[解答]
(3) 求数列 {an} 的通项公式及前n项和公式。
[解答]
25. 已知l1、l2 是过点 P(![]() ,0) 的两条互相垂直的直线,且l1、l2与双曲
,0) 的两条互相垂直的直线,且l1、l2与双曲
线 y![]() -x
-x![]() =1# 各自有两个交点,分别为A1、B1 和A2、B2。
=1# 各自有两个交点,分别为A1、B1 和A2、B2。
(1) 求l1 的斜率K1 的取值范围;( $J*1$ )
![]() ∪
∪![]() ∪
∪![]() ∪(
∪(![]() )
)
[解答]
(2) 若A1 恰是双曲线的一个顶点,求 |A2B2|的值。( $S*D$ )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
[解答]
参 考 答 案
一、
1. B
[分析解题]
m![]() -m-2=0
-m-2=0
由条件知z是纯虚数,则m应满足 得m=-1 ∴选(B)
m![]() -3m+2≠0
-3m+2≠0
2. D
3. B
[分析解题]
由 y-3=log2x 得 ![]() ,又由原函数 x≥1 得 y≥3 。
,又由原函数 x≥1 得 y≥3 。
∴选(B)
4. D
[分析解答]
化为截距式:![]() . ∴选(D)
. ∴选(D)
5. D
6. D
7. A
[分析解题]
∵ ![]() ).∴T=2π.选(A)
).∴T=2π.选(A)
8. A
[分析解题]
原式 =![]() (sin90°-sin50°+cos120°+cos40°)
(sin90°-sin50°+cos120°+cos40°)
![]() 选(A)
选(A)
9. A
10. D
[分析解答] ∵男生甲必须参加,∴只须再选出2人,由条件至少有一个女生,因此只有一个女生参加的方法种数为
![]() ·
·![]() ,有两个女生参加的方法种数 有
,有两个女生参加的方法种数 有![]() ·
·![]()
∴![]() 选(D)
选(D)
11. D
[分析解答]
代值检验。把 a=-1 代入得 y=sin2x-cos2x=![]() ,由函数周期及图象可得
,由函数周期及图象可得 ![]() 为其一条对称轴。其它值不符。∴选(D)
为其一条对称轴。其它值不符。∴选(D)
12. C
[分析解答]
抛物线方程为 ![]() 。开口向左,顶点
。开口向左,顶点![]() .
.
∴焦点 (![]() ,0) 。选(C)
,0) 。选(C)
13. B
[分析解答]
![]() 的系数为
的系数为![]() 选(B)
选(B)
14. D
|
[分析解答] 如右图, 作NE∥AM交AB于E,连CE,则∠ENC即为所求,在△NEC中, |
∴ ![]() ∴
∴ ![]()
![]() .
. ![]()
∴ ![]() . 选(D)
. 选(D)
15. D
[分析解答]
|
如右图,铁皮长为扇形所在圆的直径12cm, ∵扇形圆心角 |
∵![]() ∴宽为9cm。选(D)
∴宽为9cm。选(D)
二、
16. A
[分析解答] ∵ ![]()
∴ ![]()
![]()
![]()
![]()
![]() ......
......![]()
=![]()
![]()
17. D
[分析解答] 设圆柱底面半径为r,高为h。则有4r+2h=1.
又 V=πr![]() ·h=πr
·h=πr![]() ·
·![]()
![]() ·
·![]() ·2r·2r·(1-4r)≤
·2r·2r·(1-4r)≤![]()
![]() 。
。
∴最大体积为 ![]() π。
π。
18. C
[分析解答] 原式![]() 。
。
19. B
[分析解答] 由条件知,椭圆焦点在y轴上
![]()
依题意:
=> a=2,c=1,![]()
![]()
∴椭圆方程为![]()
三、
20. B
[分析解答]原式= 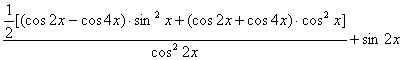
![]()
![]()
![]()
当![]() 时,y取最小值
时,y取最小值![]() 。
。![]()
21. [分析解答] 设z=a+bi(a,b∈R),则z+3 = a+bi+3
依题意![]() (1)又
(1)又![]() 其虚部
其虚部 ![]() (2)
(2)
a=-1 a=-2
由(1)、(2)求得 或 即z=-1-2i
b=-2 b=-1
或-2-i代入 z+3辐角主值不是 ![]() 。 ∴ 这样的虚数z不存在。
。 ∴ 这样的虚数z不存在。
|
22. |
(1)
[分析解答]
证:如图,设AC与BD交于点O,连接EO,则EO∥PC,
∵PC⊥平面AC。
∴平面EDB⊥平面AC。
| (2) |
[分析解答]
|
∵EO∥PC。∴EO∥平面PBC。∴点E到平面PBC的距离等于点O到平面PBC的距离。 作OH⊥BC于H。∵PC⊥平面AC。∴PC⊥OH。∴OH⊥平面PBC。 由∠ABC=60°,AB=BC ∴∠OCB=60° ∴OH=OC·sin60°= 即点E到平面PBC的距离为= (3)
[分析解答] ∵平面EDB⊥平面AC,AO⊥BD,∴AO⊥平面EDB。 作OH⊥EB于H,连结AH。则EB⊥AH。∴AHO即为 二面角A—EB—D的平面角。 ∵ |
在△EOB中,由面积公式得:![]()
![]() ,且AO⊥OH,∴
,且AO⊥OH,∴![]() .
.
∴二面角A—EB—D的正切值为![]() 。
。
23.
|
[分析解答] 如图建立坐标系。设抛物线方程为 则C点坐标为(3000,1200)代入方程 ∴(x-3000) 代入得p=3750. ∴弹道抛物线方程为(x-3000) |
当x=500时,代入方程得y≈367(m)>350(m).
∴离炮位500米处的炮弹高度大于障碍物的高度。所以能越过障碍物。
24. (1)
[分析解答]
∵Sn+1=4an+2 Sn+2=4an+1+2 两式相减得:an+2=4an+1-4an 即:an+2-2an+1=2(an+1-2an)
∴ ![]() ∵ bn=an+1-2an ∴{bn}是以2为公比的等比数列。
∵ bn=an+1-2an ∴{bn}是以2为公比的等比数列。
又由Sn=4a1+2, a1=1, a2=5得b1=a2-2a1=3 ∴bn=3·2![]()
(2) [分析解答]
∵![]() ,∴
,∴![]()
![]() 。
。
将![]() ·
·![]() 代入得
代入得![]() 。
。
(n=1, 2…) ∴ {cn}是以![]() 为公差的等差数列且
为公差的等差数列且![]() .
.
∴ ![]() 。
。
(3) [分析解答]
∵![]()
∴an=2![]() ·cn=(3n-1)·2
·cn=(3n-1)·2![]() . (n=1,2,…)
. (n=1,2,…)
又Sn=4an-1+2=4(3n-4)·2![]() +2=(3n-4)·2
+2=(3n-4)·2![]() +2
+2
当n=1时S1=a1=1适合此式
∴Sn=(3n-4)·2![]() +2(n∈N)
+2(n∈N)
25.
(1) 对
[分析解答]
依题设,l1, l2的斜率都存在,因为l1过![]() 且与双曲线有两个交点。
且与双曲线有两个交点。
故方程组 ![]() y
y![]() -x
-x![]() =1 (1)有两个不同的解
=1 (1)有两个不同的解
消去y整理得:![]() (2)
(2)
若![]() 则方程组(1)只有一个解,与题设矛盾∴
则方程组(1)只有一个解,与题设矛盾∴![]()
又![]() 时方程(2)的判别式为△1=4(3k
时方程(2)的判别式为△1=4(3k![]() -1)
-1)
同理可设l2的斜率为k2,可用同法得到
△2=4(3![]() -1) (
-1) (![]() ≠1)#。又k1·k2=-1
≠1)#。又k1·k2=-1
于是l1,l2与双曲线各有两个交点,等价于 3![]() -1>0
-1>0
![]() -1>0
-1>0
![]() <|k1|<
<|k1|<![]()
解得
k1·k2=-1 |k1|≠1
|k1|≠1 ∴k1∈(![]() ,-1)∪(-1,
,-1)∪(-1,![]() )∪(
)∪(![]() ,1)∪(1,
,1)∪(1,![]() )
)
(2) D
[分析解答]
双曲线 y![]() -x
-x![]() =1的顶点为(0,1),(0,-1)
=1的顶点为(0,1),(0,-1)
取A1(0,1)时,有![]() ,解得
,解得![]()
从而![]() .
.
记12与双曲线两交点为A2(x1,y1),B2(x2,y2)。
则由韦达定理可得|A2B2|![]() .
.
当取A1(0,-1)时,由双曲线y![]() -x
-x![]() =1的关于x轴的对称性,
=1的关于x轴的对称性,
知|A2B2|![]() . ∴ L1过双曲线的一个顶点时,|A2B2|
. ∴ L1过双曲线的一个顶点时,|A2B2|![]() .
.