二次函数综合问题例谈
北京中国人民大学附中 梁丽平
陕西省咸阳市永寿中学 安振平
二次函数是中学代数的基本内容之一,它既简单又具有丰富的内涵和外延. 作为最基本的初等函数,可以以它为素材来研究函数的单调性、奇偶性、最值等性质,还可建立起函数、方程、不等式之间的有机联系;作为抛物线,可以联系其它平面曲线讨论相互之间关系. 这些纵横联系,使得围绕二次函数可以编制出层出不穷、灵活多变的数学问题. 同时,有关二次函数的内容又与近、现代数学发展紧密联系,是学生进入高校继续深造的重要知识基础. 因此,从这个意义上说,有关二次函数的问题在高考中频繁出现,也就不足为奇了.
学习二次函数,可以从两个方面入手:一是解析式,二是图像特征. 从解析式出发,可以进行纯粹的代数推理,这种代数推理、论证的能力反映出一个人的基本数学素养;从图像特征出发,可以实现数与形的自然结合,这正是中学数学中一种非常重要的思想方法. 本文将从这两个方面研究涉及二次函数的一些综合问题.
1. 代数推理
由于二次函数的解析式简捷明了,易于变形(一般式、顶点式、零点式等),所以,在解决二次函数的问题时,常常借助其解析式,通过纯代数推理,进而导出二次函数的有关性质.
1.1
二次函数的一般式![]()
![]() 中有三个参数
中有三个参数![]() . 解题的关键在于:通过三个独立条件“确定”这三个参数.
. 解题的关键在于:通过三个独立条件“确定”这三个参数.
例1 已知![]() ,满足1
,满足1![]() 且
且![]() ,求
,求![]() 的取值范围.
的取值范围.
分析:本题中,所给条件并不足以确定参数![]() 的值,但应该注意到:所要求的结论不是
的值,但应该注意到:所要求的结论不是![]() 的确定值,而是与条件相对应的“取值范围”,因此,我们可以把1
的确定值,而是与条件相对应的“取值范围”,因此,我们可以把1![]() 和
和![]() 当成两个独立条件,先用
当成两个独立条件,先用![]() 和
和![]() 来表示
来表示![]() .
.
解:由![]() ,
,![]() 可解得:
可解得:
![]() (*)
(*)
将以上二式代入![]() ,并整理得
,并整理得
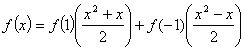 ,
,
∴ ![]() .
.
又∵![]()
![]() ,
,![]() ,
,
∴ ![]() .
.
例2 设![]() ,若
,若![]() ,
,![]() ,
,![]() , 试证明:对于任意
, 试证明:对于任意![]() ,有
,有![]() .
.
分析:同上题,可以用![]() 来表示
来表示![]() .
.
解:∵ ![]() ,
,
∴ ![]() ,
,
∴ 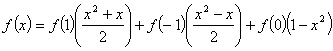 .
.
∴ 当![]() 时,
时,

当![]() 时,
时,
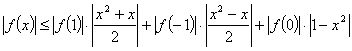
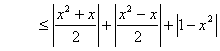
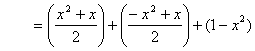
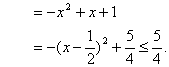
综上,问题获证.
1.2 利用函数与方程根的关系,写出二次函数的零点式![]()
例3 设二次函数![]() ,方程
,方程![]() 的两个根
的两个根![]() 满足
满足![]() . 当
. 当![]() 时,证明
时,证明![]() .
.
分析:在已知方程![]() 两根的情况下,根据函数与方程根的关系,可以写出函数
两根的情况下,根据函数与方程根的关系,可以写出函数![]() 的表达式,从而得到函数
的表达式,从而得到函数![]() 的表达式.
的表达式.
证明:由题意可知![]() .
.
![]() ,
,
∴ ![]() ,
,
∴ 当![]() 时,
时,![]() .
.
又![]() ,
,
![]()
∴ ![]() ,
,
综上可知,所给问题获证.
1.3 紧扣二次函数的顶点式![]() 对称轴、最值、判别式显合力
对称轴、最值、判别式显合力
例4 已知函数![]() 。
。
(1)将![]() 的图象向右平移两个单位,得到函数
的图象向右平移两个单位,得到函数![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)函数![]() 与函数
与函数![]() 的图象关于直线
的图象关于直线![]() 对称,求函数
对称,求函数![]() 的解析式;
的解析式;
(3)设![]() ,已知
,已知![]() 的最小值是
的最小值是![]() 且
且![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
解:(1)![]()
(2)设![]() 的图像上一点
的图像上一点![]() ,点
,点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,由点Q在
,由点Q在![]() 的图像上,所以
的图像上,所以
![]() ,
,
于是 ![]()
即 ![]()
(3)![]() .
.
设![]() ,则
,则![]() .
.
问题转化为:![]() 对
对![]() 恒成立. 即
恒成立. 即
![]() 对
对![]() 恒成立. (*)
恒成立. (*)
故必有![]() .(否则,若
.(否则,若![]() ,则关于
,则关于![]() 的二次函数
的二次函数![]() 开口向下,当
开口向下,当![]() 充分大时,必有
充分大时,必有![]() ;而当
;而当![]() 时,显然不能保证(*)成立.),此时,由于二次函数
时,显然不能保证(*)成立.),此时,由于二次函数![]() 的对称轴
的对称轴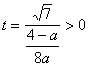 ,所以,问题等价于
,所以,问题等价于![]() ,即
,即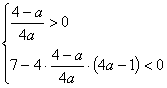 ,
,
解之得:![]() .
.
此时,![]() ,故
,故![]() 在
在![]() 取得最小值
取得最小值![]() 满足条件.
满足条件.
2. 数形结合
二次函数![]() 的图像为抛物线,具有许多优美的性质,如对称性、单调性、凹凸性等. 结合这些图像特征解决有关二次函数的问题,可以化难为易.,形象直观.
的图像为抛物线,具有许多优美的性质,如对称性、单调性、凹凸性等. 结合这些图像特征解决有关二次函数的问题,可以化难为易.,形象直观.
2.1 二次函数的图像关于直线![]() 对称, 特别关系
对称, 特别关系![]() 也反映了二次函数的一种对称性.
也反映了二次函数的一种对称性.
例5 设二次函数![]() ,方程
,方程![]() 的两个根
的两个根![]() 满足
满足![]() . 且函数
. 且函数![]() 的图像关于直线
的图像关于直线![]() 对称,证明:
对称,证明:![]() .
.
解:由题意
![]() .
.
由方程![]() 的两个根
的两个根![]() 满足
满足![]() , 可得
, 可得
![]() 且
且![]() ,
,
∴ ![]() ,
,
即 ![]() ,故
,故 ![]() .
.
2.2 二次函数![]() 的图像具有连续性,且由于二次方程至多有两个实数根. 所以存在实数
的图像具有连续性,且由于二次方程至多有两个实数根. 所以存在实数![]() 使得
使得![]() 且
且![]()
![]() 在区间
在区间![]() 上,必存在
上,必存在![]() 的唯一的实数根.
的唯一的实数根.
例6 已知二次函数![]() ,设方程
,设方程![]() 的两个实数根为
的两个实数根为![]() 和
和![]() .
.
(1)如果![]() ,设函数
,设函数![]() 的对称轴为
的对称轴为![]() ,求证:
,求证:![]() ;
;
(2)如果![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
分析:条件![]() 实际上给出了
实际上给出了![]() 的两个实数根所在的区间,因此可以考虑利用上述图像特征去等价转化.
的两个实数根所在的区间,因此可以考虑利用上述图像特征去等价转化.
解:设![]() ,则
,则![]() 的二根为
的二根为![]() 和
和![]() .
.
(1)由![]() 及
及![]() ,可得
,可得 ![]() ,即
,即![]() ,即
,即
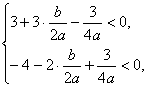
两式相加得![]() ,所以,
,所以,![]() ;
;
(2)由![]() , 可得
, 可得 ![]() .
.
又![]() ,所以
,所以![]() 同号.
同号.
∴ ![]() ,
,![]() 等价于
等价于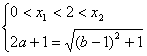 或
或 ,
,
即 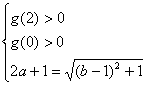 或
或
解之得 ![]() 或
或![]() .
.
2.3 因为二次函数![]() 在区间
在区间![]() 和区间
和区间![]() 上分别单调,所以函数
上分别单调,所以函数![]() 在闭区间上的最大值、最小值必在区间端点或顶点处取得;函数
在闭区间上的最大值、最小值必在区间端点或顶点处取得;函数![]() 在闭区间上的最大值必在区间端点或顶点处取得.
在闭区间上的最大值必在区间端点或顶点处取得.
例7 已知二次函数![]() ,当
,当![]() 时,有
时,有![]() ,求证:当
,求证:当![]() 时,有
时,有![]() .
.
分析:研究![]() 的性质,最好能够得出其解析式,从这个意义上说,应该尽量用已知条件来表达参数
的性质,最好能够得出其解析式,从这个意义上说,应该尽量用已知条件来表达参数![]() . 确定三个参数,只需三个独立条件,本题可以考虑
. 确定三个参数,只需三个独立条件,本题可以考虑![]() ,
,![]() ,
,![]() ,这样做的好处有两个:一是
,这样做的好处有两个:一是![]() 的表达较为简洁,二是由于
的表达较为简洁,二是由于![]() 正好是所给条件的区间端点和中点,这样做能够较好地利用条件来达到控制二次函数范围的目的.
正好是所给条件的区间端点和中点,这样做能够较好地利用条件来达到控制二次函数范围的目的.
要考虑![]() 在区间
在区间![]() 上函数值的取值范围,只需考虑其最大值,也即考虑
上函数值的取值范围,只需考虑其最大值,也即考虑![]() 在区间端点和顶点处的函数值.
在区间端点和顶点处的函数值.
解:由题意知:![]() ,
,
∴ ![]() ,
,
∴ ![]()
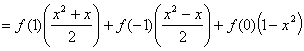 .
.
由![]() 时,有
时,有![]() ,可得
,可得 ![]()
![]()
![]() .
.
∴ ![]() ,
,
![]() .
.
(1)若![]() ,则
,则![]() 在
在![]() 上单调,故当
上单调,故当![]() 时,
时,
![]()
∴ 此时问题获证.
(2)若![]() ,则当
,则当![]() 时,
时,
![]()
又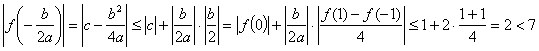 ,
,
∴ 此时问题获证.
综上可知:当![]() 时,有
时,有![]() .
.