高三数学专题复习-----函数(三)

一 基础知识

(1)基本函数性质(一次函数,二次函数,幂函数,指数函数,对数函数,),(2)函数图象变换.

二 例题

1、已知0<x<y<1,a=log_x(x+1),b=log_y(y+1),则a,b的大小关系是（　）

（A）a>b　　　　 (B)a=b　　　　　 (C)a<b　　　　 (D) 不能确定

2、若集合A＝为单元集,则实数a等于（　）

（A）2　　　　(B)－2　　　　  (C)0或2　　　　(D) －2或2

3、设二次函数f(x)=ax²+bx+c,如果f(x₁)=f(x₂)(x₁≠x₂),则f(x₁+x₂)等于（　）

（A）　　　　(B)－　　　　  (C)c　　　 (D)

4、已知抛物线f(x)=ax²+bx+c　(a<0) 的顶点坐标为（0,k），P= f()

Q= f()(m∈R),则（　）

（A）P≥ Q　　　　(B)P ≤Q　　　　　 (C)P≠Q　　　　(D) 不能确定

5、函数f(x)=的值域是(－∞，+∞)，则实数k的取值范围是(　)

（A (B) 　 (C) 　　　　　 (D)

6、已知定义在R上的函数y=f(x),对任意x∈R都有f(x－1)＝f(1－x)，那么f(x)的图象有对称轴(　)

（A）x=0　　　　  (B)x=1　　　　　 (C)y=0　　　　  (D) y=1

7、把函数f(x),的图象向左、向下分别平移2个单位，得到函数y=2^x的图象，则（　）

（A）f(x)=2^x+2+2　　(B) f(x)= 2^x+2－2　　　 (C) f(x)＝2^x－2+2　　　(D) f(x)＝2^x－2－2　

8、函数f(x)定义在实数集R上，f(x+y)=f(x)+f(y),且当x>0时，f(x)<0则f(x)  (　　)

　(A)是奇数且在R上是单调增函数　　　(B)是奇数且在R上是单调减函数

　(C)是偶函数且在R上是单调减函数　　(D)是偶函数且在R上不是单调函数

9、设函数，若函数的图象与的图象关于直线对称，则等于(　)

（A）　　　（B）　　　　（C）　　　　（D）

10、已知函数y＝f (2x)的图象，作y＝f (1－2x)的图象时，应将y＝f (2x)的图象（　）

  （A）先向右平移1个单位，再作y轴的对称图形　

  （B）先向左平移1个单位，再作y轴的对称图形

  （C）先向右平移个单位，再作y轴的对称图形

  （D）先向左平移个单位，再作y轴的对称图形

11、如果函数y＝的图象关于点A(1, 2)对称，那么（　）。

　（A）p＝－2, n＝4　 （B）p＝2, n＝－4　（C）p＝－2, n＝－4 （D）p＝2, n＝4

12、已知a>0且a≠1, 函数y＝a^－x与y＝log _a(－x)的图象只能是（ ）

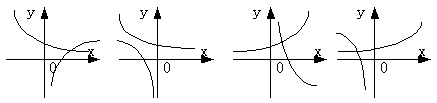　　（A）　　　　  （B）　　　　　 （C）　　　　 （D）

13、已知函数f(x)= ，若f(a) >f(2.5),则a的取值范围是　　　　　　　

14、若f(2^2x+1)=1－x,则f(8)=　　　　　　 

15、已知A＝，B＝，若A∩B=φ,则实数k的取值范围是　　　　　　　  

16、已知函数f(x)＝x²+bx+c满足f (-1+x)＝f (-1-x),且f(0)=3当x≠0时,试比较f(b^x)与f(c^x)的大小.

17、设函数f(x)=  g(x)= (a>0且a≠1)，在f(x) 和g(x)的公共定义域内比较与的大小