高三数学专题复习-----函数(二)
一 基础知识
(1)函数单调性(2)函数奇偶性(3)函数周期性
二 例题
1、若函数f(x)= ![]() 是奇函数,则m的值是( )
是奇函数,则m的值是( )
(A)0 (B)1 (C)2 (D)4
2、若函数f(x)= ![]() 上有f(x)>0,则f(x)的递增区间是( )
上有f(x)>0,则f(x)的递增区间是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3、已知y=f(2x+1)为偶函数,则函数y=f(2x)的图像的对称轴是( )
(A)x=-1 (B)x=1 (C)x=![]() (D)x=-
(D)x=-![]()
4、如果奇函数f(x)在区间![]() 上是增函数,且最小值是5,那么f(x)在区间
上是增函数,且最小值是5,那么f(x)在区间![]() 上是( )
上是( )
(A) 增函数且最小值为-5 (B)增函数且最大值为-5
(C)减函数且最小值为-5 (D)减函数且最大值为-5
5、设f(x)为定义在R上的偶函数,且f(x)在![]() 上为增函数,则f(-π) ,f(-2) ,f(3)的大小顺序是( )
上为增函数,则f(-π) ,f(-2) ,f(3)的大小顺序是( )
(A)f(3)< f(-2) <f(-π) (B)f(-π)< f(-2)< f(3)
(C)f(-2)< f(3) <f(-π) (D)f(-π)< f(3)< f(-2)
6、已知![]() 在区间
在区间![]() 上是x的减函数,则a的取值范围是( )
上是x的减函数,则a的取值范围是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
7、已知函数f(x)在![]() 上是增函数,函数f(x+2)是偶函数,则下列结论中正确的是( )
上是增函数,函数f(x+2)是偶函数,则下列结论中正确的是( )
(A)f(1)< f(![]() ) <f(
) <f(![]() )
(B)f(
)
(B)f(![]() )< f(1)< f(
)< f(1)< f(![]() )
)
(C)f(![]() )< f(
)< f(![]() ) <f(1)
(D)f(
) <f(1)
(D)f(![]() )< f(1)< f(
)< f(1)< f(![]() )
)
8、已知f(x)是定义在R上的偶函数,且是周期为2的周期函数,当x∈![]() 时,f(x)=x则f(
时,f(x)=x则f(![]() )的值为( )
)的值为( )
(A)![]() (B)
(B)![]() (C)-
(C)-![]() (D)-
(D)-![]()
9、已知定义在R上的奇函数f(x)在![]() 上是增函数,且f(
上是增函数,且f(![]() )=0,则不等式f(
)=0,则不等式f(![]() )>0的解集是( )
)>0的解集是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10、已知y=f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2-2x,则在R上
f(x)的表达式为( )
(A)-x(x-2) (B)![]() (C)
(C)![]() (D)
(D)![]()
11、设![]() 若f(
若f(![]() )=5,则f(lg3)=
)=5,则f(lg3)=
12、已知y=f(x)是定义在R上的偶函数,且![]() 若当x∈
若当x∈![]() 时,f(x)=x则f(5.5)=
时,f(x)=x则f(5.5)=
13、已知y=f(x)是定义在R上的奇函数,且f(x-2)=-f(x),给出下列四个结论:
①f(2)=0; ② f(x)是以4为周期的函数; ③f(x)的图象关于直线x=0对称; ⑷f(x+2)=f(-x) .其中所有正确结论的序号是
14、关于函数![]() 有下列命题:
有下列命题:
①其图像关于y轴对称 ② 当x>0时,f(x)是增函数;当x<0时,f(x)是减函数 ③f(x)的最小值是lg2; ⑷当-1<x<0或x>2时,f(x)是增函数 ⑤ f(x)无最大值,也无最小值。 其中所有正确结论的序号是
15、已知函数f(x)=6x2-mx+5在区间[-2,+∞)上是增函数,则f(1)的取值范围是
16、已知![]()
(I)求f(x)的定义域;
(II)判断f(x)的奇偶性并予以证明;
(III)求使f(x)>0的x的取值范围。
17、设函数![]() 求f(x)的单调区间,并证明f(x)在其单调区间上的单调性
求f(x)的单调区间,并证明f(x)在其单调区间上的单调性
18、函数![]() 在(-∞,1]上有意义,求实数a的取值范围。
在(-∞,1]上有意义,求实数a的取值范围。
19、设函数![]() 求a的取值范围使函数f(x)在区间[0,+∞)上是单调函数
求a的取值范围使函数f(x)在区间[0,+∞)上是单调函数
20、定义在[-2,2]上的偶函数g(x),当![]() 时g(x)单调递减,若g(1-m)< g(m),求m的取值范围。
时g(x)单调递减,若g(1-m)< g(m),求m的取值范围。
21、已知函数![]() 是R上的增函数,求a的取值范围。
是R上的增函数,求a的取值范围。
22、若函数![]() (a,b,c∈Z+)是奇函数,又f(1)=3,f(3)<7.
(a,b,c∈Z+)是奇函数,又f(1)=3,f(3)<7.
(I)求a,b,c的值;
(II)用函数单调性定义判定x<0时,f(x)的增减性;并写出x>0时的增减区间.
23、已知f (x)=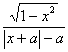 (a∈R), (I) 求函数y=f (x)的定义域;(II) 判断函数y=f (x) 的奇偶性;(III) 当a为何值时,f (x)为奇函数?当y= f (x)为奇函数时,确定其单调性。
(a∈R), (I) 求函数y=f (x)的定义域;(II) 判断函数y=f (x) 的奇偶性;(III) 当a为何值时,f (x)为奇函数?当y= f (x)为奇函数时,确定其单调性。