数学能力训练之六（探索问题）

要点：需要灵活与综合地运用基础知识、基本技能和数学思想方法去探索条件、结论及其内联系，有利于形成良好的思维品质和培养创造性分析问题和解决问题的能力。

1、　末给出结论的探索问题：归纳型。

2、　对结论不确定的探索性：存在型。

一、　　　　　　　　　　　　　　　　　　 填空题：

1、　若两条异面直线a , b成80⁰角，过空间一点P的直线a , b与成¶角，这样直线不少两条， 则¶的取值范围是　　　　　　　　　　　　　　

 

2、　使函数f(x)=log_a(ax²-x)在区间[2，4]上是增函数的实数a值的集合为 　　　　 

 

 

3、　凸n棱柱有f(n)个对角面，则F(n+1)=f(n)+　　　　　　　 

4、　设f(x)=,若êf(a)f(b)ê<1,则êa+bê与ê1+abê的大小关系是　　　　　

5、　　　　　　　

6、　已知xÎ(-1,1),f_n(x)=1+2x+3x²++nx^n-1且f(x)=f_n(x)则f(x)=　　　 （最简形式）

7、　如果，则m=　　 ,n=　　　　

8、　已知数列1，2，2，3，3，3，4，4，4，4，¼，则a₁₀₀=　　　　

9、　若关于x的方程x²+ax+1=0和x²⁺+bx+1=0(a¹b)的四个根可以排成一个以2为公比的等比数列，则ab=　　　

10、　　　  如右图，ab=CD，A，B是直线L上两点，A，B在内的射影分别为A₁，B₁两点，当直线L满足条件　　　 时， CD^A₁B₁（注填上一种可以）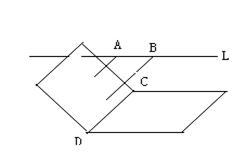

 

11、　　　  设f(x)=，若f(a)f(b)<1, 则a+b与1+ab的大小关系是　　　

（1）　　　 写出数列{b_n}的前四项；

（2）　　　 求数列{b_n}的通项公式；

（3）　　　 是否存在非零常数p,q,使得数列{}成等差数列? 若存在，求的关系式；若不存在，说明理由。

12、　　　  在RtDABC中，ÐACB=90⁰，顶点A，B，C在平面a上的射影依次为A^‘，B^’C^‘，A^‘，B^’，C^‘三点不共线。

（1）　　　 试给出一个使A^‘B^‘C^’是以C^‘为直角顶点的直角三角形的充要条件，并给出证明；

（2）　　　 判断命题的直假：DA^‘B^‘C^’不可能是锐角三角形。

13、　　　  已知OC过定点A（a,0）（a>0），圆心C在抛物线P：y²=2ax上运动，MN为OC在y轴上截得的弦，其中a为定值。

（1）　　　 试判断弦MN的长是否随圆心C运动变化？证明你的结论；

（2）　　　 当OA是OM和ON的等差中项时，试判断OC与抛物线P的准线的位置关系。

14、　　　  设a,bÎR⁺且a+b=2k (k为常数),若(a+²恒成立

　　　(1)求证：k²ab³4k²+1

　(2)求k的取值范围。

15、　　　  设f(x)=--x²+x+a (a为实常数，且a£)，是否存在实数m,n(m<n)当f(x)的定义域为[m,n]时，f(x)的值域恰为[3m,3n]?说明理由。

16、过点A（4，-2）任作一直线L与抛物线y²=2x相交于两个不同的点P，Q，抛物线y²=2x上是否存在定点B，使ÐPBQ总等于90⁰？证明你的结论。