数学能力专题训练一（选择题解法）

要点：①充分利用题干和选择支两方面提供的信息，快速、准确地作出判断，是解选择题的基本策略。

②解选择题的基本思想是：既要看到通常各类常规题的解题思想，原则上都可以指导选择题的解答；更应看到。根据选择题的特殊性，必定存在着若干异于常规题的特殊解法。我们需把这两方面有机地结合起来，对具体问题具体分析。

一、直接求解法：由因导果，对照结论。

1．已知f(x)=x(sinx+1)+ax²,f(3)=5,则f(－3)=(　 )

　(A)－5　　　 (B)－1　　 (C)1　　　　(D)无法确定

2．若定义在实数集R上的函数y=f(x+1)的反函数是y=f^－1(x－1),且f(0)=1,则f(2001)　　的值为(　)

　(A)1　　　　 (B)2000　  (C)2001　　 (D)2002

3.已知奇函数f(x)满足：f(x)=f(x+2)，且当x∈(0,1)时，f(x)=2^x－1,则的值为

　 （A）　　（B）　　　　（C）　　  （D）

　　

4．已知两点M(1,),给出下列曲线方程：①4x+2y－1=0;②x²+y²=3;③;　 ④.在曲线上存在点P满足MP=NP的所有曲线方程是（　）

（A）①③　　（B）②④　　　　  （C）①②③ 　　　 （D）②③④

5．设a>b>c,n∈N,且恒成立，则n的最大值是（　）

(A)2　　　　  (B)3　　　　　  (C)4　　　　　　 (D)5

6.如果把y=f(x)在x=a及x=b之间的一段图象近似地看作直线的一段，设a≤c≤b，那么f(c)的近似值可表示为（　）

(A)　　　　　　 (B)

(C)　 (D)  

二、逆推验证法：执果索因，逆推检验。

7．若不等式0≤x²－ax+a≤1的解集是单元素集，则a的值为（  ）

 (A)0　　　  (B)2　　　　　 (C)4　　　　(D)6

8.对于函数f(x),x∈[a,b]及g(x), x∈[a,b]。若对于 x∈[a,b],总有

 ，我们称f(x)可被g(x)替代.那么下列给出的函数中能替代f(x)=, x∈[4,16]的是(　)

(A)g(x)=x+6, x∈[4,16]　　　　　 (B)g(x)=x²+6, x∈[4,16]

(C)g(x)=, x∈[4,16]　　　　　  (D)g(x)=2x+6, x∈[4,16]

 9.在下列图象中，二次函数y=ax²+bx与指数函数的图象只可能是（　）

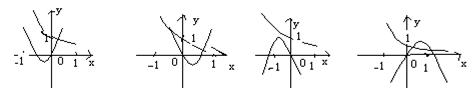　　  (A)　　　　　　　   (B)　　　　　　  (C)　　　　　　　 (D)

　 10.已知复数z满足arg(z+1)=，arg(z－1)= ,则复数z的值是(　)

(A)　　  (B) 　　(C) 　　(D)

　 11．已知复数z满足z+z·,则复数z的值是(　)

(A)　　　 (B)　　 (C)　　 (D)

　12.f(x)是定义在R上的奇函数,且f(3－x)=f(3+x),若 x∈(0,3)时f(x)=2^x,则f(x)在(－6,－3)上的解析式是f(x)=（　）

（A）2^x+6　　　（B）－2^x+6　　 （C）2^x　　　 （D）－2^x

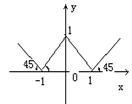
  13.已知y=f(x)的图象如右，那么f(x)=(　)

　 (A)　　 (B)　　(C)x²－2x+1　(D)x²－1

三、特例检验法：取满足条件的特例（特殊值、特殊点、特殊图形等）进行推证。

14．如果函数y=sin2x+a cos2x的图象关于直线x=－对称，那么a=(  )

(A)　　　　 (B)－　　　　 (C)1　　　　  (D)－1

15.已知f(x)=+1(x≥1).函数g(x)的图象沿x轴负方向平移1个单位后，恰好与f(x)的图象关于直线y=x对称，则g(x)的解析式是（　）

（A）x²+1(x≥0)　　(B)(x－2)²+1(x≥2)　 (C) x²+1(x≥1)　 (D) (x+2)²+1(x≥2)

　　

16.直三棱柱ABC—A^/B^/C^/的体积为V，P、Q分别为侧棱AA^/、CC^/上的点，且AP=C^/Q，则四棱锥B—APQC的体积是（　）

　（A）　　　　（B）　　  （C）　　　　 （D）

17．在△ABC中，A=2B，则sinBsinC+sin²B=(　 )

　 (A)sin²A　  　　(B)sin²B　　　　 (C)sin²C　　　　  (D)sin2B

18.若(1-2x)⁸=a₀+a₁x+a₂x²+…+a₈x⁸,则a₀+a₁+a₂+…+a₈=(　)

　 （A）1　　　 （B）－1　　　　  （C）3⁸－1　　　　 （D）2⁸－1

19．数列1,1+2,1+2+2²,…,1+2+2²+…+2^n－1,…的前99项的和是（　 ）

　（A）2¹⁰⁰－101　（B）2⁹⁹－101　　　（C）2¹⁰⁰－99　　　（D）2⁹⁹－99

四、逻辑分析法：（1）若（A）真（B）真，则（A）必排出，否则与“有且仅有一个正确结论”相矛盾.　 (2) 若（A）（B），则（A）（B）均假。　（3）若（A）（B）成矛盾关系,则必有一真,可否定(C)(D).

20.平行六面体ABCD—A₁B₁C₁D₁的两个对角面ACC₁A₁与BDD₁B₁都是矩形,则这个平行六面体是(　)

 (A)正方体　　 (B)长方体　　 (C)直平行六面体　　 (D)正四棱柱

　　

21.当x∈[-4,0]时恒成立,则a的一个可能值是(　)

(A)5　　　　  (B)-5　　　　 (C)　　　　  (D)

22.已知z₁=a₁+b₁i,z₂=a₂+b₂i(a_1,a₂,b₁,b₂均为实数)是两个非零复数,则它们所对应的向量与互相垂直的充要条件是(　)

 (A)　 (B) a₁a₂+b₁b₂=0　 (C)z₁-iz₂=0　　 (D)z₂-iz₁=0

五、数形结合法:明确条件及结论的几何意义,借助直观图形肯定或否定.

　 23.方程lg(x+4)=10^x的根的情况是(　)

(A)仅有一根　　 (B)有一正一负根　　 (C)有两负根　　 (D)无实根

　 24.E、F分别是正四面体S—ABC的棱SC、AB的中点,则异面直线EF与SA所成的角是

(A)90^o　　　　  (B)60^o　　　　　 (C)45^o　　　　　  (D)30^o

　 25.已知x₁是方程x+lgx=3的根,x₂是方程x+10^x=3的根,那么x₁+x₂的值是(　)

(A)6　　　　　 (B)3　　　　　　 (C)2　　　　　  (D)1

　 26.已知函数f(x)=x²,集合A={xf(x+1)=ax,x∈R},且A∪=,则实数a的取值范围是

(A)(0,+∞)　　　(B)(2,+∞)　　　　(C)　　(D)

　 27.函数f(x)=在区间(-2,+ ∞)上为增函数,则a的取值范围是(　)

(A)0<a<　  (B)a<-1或a>　　  (C)a>　　　 (D)a>-2

　28.已知函数f(x)=3-2x,g(x)=x²-2x,构造函数F(x),定义如下:当f(x)≥g(x)时,F(x)=g(x);当f(x)<g(x)时,F(x)=f(x).那么F(x)

　(A)有最大值3,最小值-1　　　　　　　　 (B)有最大值7-2,无最小值

　 (C) 有最大值3,无最小值　　　　　　 (D) 无最大值,也无最小值

　 29．ω是正实数，函数f(x)=2sinωx在上递增，那么(　)

(A)0<ω<　　  (B)0<ω≤2　　　(C)0<ω≤　 (D) ω≥2

六、特征分析法：抓住题中的位置特征、数值特征、结构特征进行推理。

　 30．若关于x的方程=k(x-2)有两个不等实根，则实数k的范围是（　）

(A)　(B)　(C)　(D)

　

　 31.设S为半径等于1的圆内接三角形的面积，则4S+的最小值为（　）

(A)　　　　(B)　　  (C)7　　　　(D)

　 32．若关于x的不等式x-sin²θ+x+cos²θ<k的解集非空，则实数k的取值范围是（　 ）

　　(A)k≥1　　　　 (B)k>1　　　 (C)0<k<1　　　  (D)0<k≤1

　 33.将抛物线y=x²－4x+3绕其顶点顺时针旋转90^o，则抛物线方程为（　）

（A）(y+1)²=2－x （B）(y+1)²=x－2 （C）(y－1)²=2－x （D）(y－1)²=x－2

 

　 34.若复数z满足z+=1，则z的模的范围是（　）

(A) (B) (C)  (D)

　

　 35.把函数y=cos2x+sin2x的图象经过变换得到y=-2sin2x的图象，这个变换是（　）

（A）向左平移个单位　　　　  （B）向右平移个单位

（C）向左平移个单位　　　　　 （D）向右平移个单位

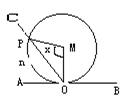
36．如图，半径为2的⊙M切直线AB于O点，射线OC从OA出发绕O点顺时针方向旋转到OB。旋转过程中，OC交⊙M于P，记∠PMO为x，弓形PnO的面积为S=f(x)，那么f(x)的图象是

(A)　　　　　　　 (B)　　　　　　  (C)　　　　　　　 (D)