数学能力专题训练三（综合题解法）

要点：所谓综合题，是泛指题目本身或在解题过程中，涉及多个知识点和多种数学思想方法、具有较高能力要求的数学题.

如下,我们从八个方面举例,对综合题的解题策略作一探讨.

一、从条件入手——分析条件，化繁为简，注重隐含条件的挖掘.

1.已知ΔABC的外接圆半径为R,并且有2R(sin²A-sin²C)=(a-b)sinB,求ΔABC的面积的最大值.

　

　2.是否存在实数a(a>0且a≠1)，使方程log_a(4x²-4ax)-2log_a(2x-a+1)=0有解?若存在,求出a的取值范围和方程的解;若不存在,说明理由.

3.设z是虚数，ω=z+是实数，且-1＜ω＜ 2.(1)求z的值及z的实部的取值范围; (2)设,求证:u是纯虚数;(3)求ω-u²的最小值.

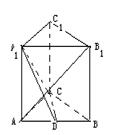 4.已知直三棱柱ABC-A₁B₁C₁中,AC=BC,D为AB的中点,异面直线BC₁与AB₁互相垂直.(1)求证:AB₁⊥平面A₁CD;(2)若CC₁与面ABB₁A₁的距离为1,A₁D=2,AB₁=2,求三棱锥A₁-ACD的体积.

　　　　 

二、从结论入手---执果索因,搭好联系条件的桥梁.

5.已知函数f(x)是定义在R上的增函数,当θ∈[0,]时,是否存在这样的实数m,使f(4m-2mcosθ)>f(3-cos2θ)对所有θ∈[0,]均成立?若存在,求出所有适合条件的实数m;若不存在,说明理由.

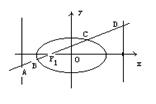6.已知椭圆,过其左焦点F₁且斜率为的直线与椭圆及其准线的交点从左到右依次为A、B、C、D,记f(m)=AB-CD.(1)求f(m)的解析式;(2)求 f(m)的最大值和最小值.

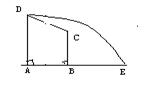7.如图,在直角梯形ABCD中,AD=3,AB=4,BC=,曲线DE上任一点到A、B两点距离之和都相等.(1)适当建立坐标系,求曲线DE的方程;(2)过点C能否作一条与曲线DE相交且以C为中点的弦?若能,求出弦所在的直线方程;若不能,说明理由.

　　　　　　　　 

三、　　　 回到定义和图形中来.

　 8.已知椭圆的一个焦点和一条准线与抛物线y²=8(x+2)的焦点和准线分别重合.(1)求椭圆短轴端点的轨迹C;(2)过点A（-4，0）、斜率为k的直线l与C交于第一象限内的两点P、Q，定点B（0，8）与PQ的中点M的连线交x轴于点N，若点N位于点A左侧，求k的取值范围.

　9.已知复数z₁=+I,z₂=r(cosθ+isinθ)(r>0,0<θ<π),z₃=z₁z₂.若z₁-z₂=r+1,求r和θ的取值范围.

　10.已知f(θ)=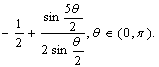(1)将f(θ)表示为关于cosθ的多项式;(2)试求曲线y=kcosθ+k与曲线y=f(θ)至少有一个公共点时k的取值范围.

 

　　　　　　　　　　　　　

11.已知数列{a_n}的前n项和S_n=1-na_n(n∈N).(1)试求a₁,a₂,a₃;;(2)写出数列{a_n}的通项公式,并用数学归纳法证明.

四、以简单的、特殊的情况为突破口.

　 12.设a_n=　　求证:　 (1)a_n=1+

(2)　　  (3)

 

 13.已知抛物线C的顶点在原点,焦点在轴上,ΔABC的重心在抛物线的焦点上,且三个顶点均在抛物线上,若BC所在的直线方程为 4x-y-20=0,(1)求抛物线C的方程;(2)是否存在定点M,使过点M的动直线l与C交于P,Q,且∠POQ恒为直角?证明你的结论.

　　　　　　　　　　　　 

  五、构造辅助问题(函数、方程、图形……),换一个角度去思考.

　 14.(1)已知a、b、c是ΔABC的三边,求证:

(2)已知f(t)=log₂t,,对于f(t)值域内的所有实数m,不等式x²+mx+4>2m+4x都能成立,求x的取值范围.

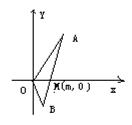
　15.如图,线段AB过x轴正半轴上一定点M(m,0),端点A,B到x轴距离之积为2m,以x轴为对称轴,过A,O,B三点作抛物线.(1)求抛物线方程;(2)若tg∠AOB=--1,求m的取值范围.

 

 16.若对一切实数p,p<2,不等式(log₂x)²+plog₂x+1>2log₂x+p恒成立,求实数x的取值范围.

　　　　　　　　　　  　　　 

  17.直线l: 5x—7y—1=0交以坐标轴为对称轴的双曲线C于A、B两点,定点P(5,14)与A,B构成以AB为斜边的等腰直角三角形,求双曲线C的方程.

  六、通过横向沟通和转化,将各数学分支中不同的知识点串联起来.

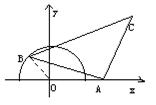　18.如图，B是半圆O上的动点，OB=1，OA=2，△ABC是等腰直角三角形，BC为斜边，试求O，C两点之间距离的最大值。

  19．复数z₁,z₂对应于复平面内的点A，B，且满足条件：（1）z₁=riz₂(r∈R且r≠0);（2）z₁+z₂+z₁-z₂=10,求△AOB面积的最大值.

　　　　　　　　　　　　　  

七、培养整体意识，把握整体结构。

　 20．求同时满足下列两个条件的复数z: (1)(2)z的实部和虚部都是整数。

  21．设函数试证明：

(1)　  存在两个实数m₁,m₂(m₁<m₂)，满足

(2)　  (1－m₁)(1－m₂)=－a²;　　　　　 (3)

八、连续性问题——承上启下,层层递进,充分利用已得出的结论.

　 22.已知ΔABC中，a,b,c三边成等差数列。

(1)　　证明：　(2)求的值；

(2)　　求cosA+2cosB+cosC的值；(4)求cosA+cosC－cosAcosC+sinAsinC的值；

　　　　　　　　　　　　　　 

23.已知动点P与双曲线的两个焦点所连线段的和为定长,且这两条线段夹角的余弦值之最小值是.(1)求动点P的轨迹方程;(2)在x轴的正半轴上求一点Q,使点Q与这轨迹上的点的最近距离为1.

 24.已知ΔABC三个内角A,B,C满足A+C=2B,设

x=cos,f(x)=cosB(.(1)试求f(x)的解析式及其定义域;(2)在定义域内讨论这个函数的单调性,并加以证明;(3)求这个函数的值域.

　25.(1)已知a>0,a≠1,k∈R,求函数y=lg(a^x-k•2^x)的定义域;

　　 (2)已知F(x)=2若方程F(x)=0有解,求k的取值范围.