如皋市磨头中学高三期末模拟考试 数学试题 命题人 丁东进
一. 选择题:(题共12小题, 每小题5分，共60分)
1. 已知集合
Z为整数集, 则
等于
( )
A. 
B. 
C. 
D. 
2. 
的值等于 ( )
A. 
B. 
C. 
D.
3. 在等比数列
中, 
, 则
的值为 ( )
A. 48 B. 72 C. 144 D. 192
4. 已知实数x、y满足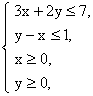
则
的最大值是
( )
A. 0 B. 4 C. 7 D. 11
5. 设a、b、c表示三条直线, 
、
表示两个平面, 则下列命题中逆命题不成立的是
( )
A. 已知
若
则∥ B. 已知
, c是a在内的射影, 若b
c, 则a
b
C. 已知
,, 若∥, 则c∥b D. 已知, 若
则
6. 下列四个函数中, 同时具有性质: ①最小正周期为
; ②图象关于直线
对称的函数是
( )
A. 
B.
C. 
D.
7. “
”是“函数
的值恒为正值”的
( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分又不必要条件
8. 在等差数列中, 前n项和为
, 
, 则
是
(
)
A. 
B. 
C. 
D.
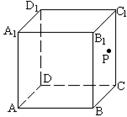9. 如图, 在正方体ABCD—A1B1C1D1中, P是侧面BB1C1C内一动点,
若点P到直线BC的距离是点P到直线C1D1距离的2倍, 则动点P的轨迹所在的曲线是
(
)
A. 直线 B. 椭圆 C. 双曲线 D. 抛物线
10. 设
, 则二次曲线
的离心率的取
值范围是 ( )
A. 
B.
C.
D. 
11. 关于函数
有下列三个命题: ⑴对于任意
,都有
⑵
在
上是减函数;⑶对于任意
,
,都有
其中正确的命题个数是
( )
A. 0 B. 1 C. 2 D. 3
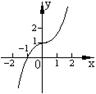
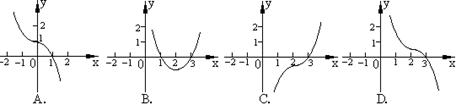12. 方程
的曲线如左图所示, 那么方程
的曲线是 ( )
如皋市磨头中学高三期末模拟考试答案页
数学试题
二. 填空题：(本大题共6小题；每小题4分，共24分)
13. 不等式
的解集为
.
14. 已知圆C的圆心在第一象限, 与x轴相切于点
, 且与直线
也相切, 则该圆的方程为 .
15. 已知O为原点, 
, 
, 
, 则
的最小值是 .
16． 在中学数学中，从特殊到一般，从具体到抽象是常见的一种思维形式。如从指数函数中可抽象出
的性质；从对数函数中可抽象出
的性质。那么从函数
(写出一个具体函数即可)可抽象出
的性质。
17．在平面几何中ΔABC的∠C内角平分线CE分AB所成线段的比
把这个结论类比到空间：在三棱锥A—BCD中（如图）DEC平分二面角A—CD—B且与AB相交于E，则得到类比的结论是
.
18．已知数列满足
, 若
,则
.
三. 解答题：(本大题5小题，共66分)
19．（12分）若f(x)是定义在（0，+∞）上的增函数，且对一切x>0,y>0满足f(x/y)=f(x)-f(y)
①求f(1);②若f(2)=1,解不等式f(x+3)-f(1/x)<2;
20．(12分)已知向量
,
, 
.
(1) 求a·b及
;
(2) 若
(其中
)的最小值是
, 求
的值.
21．(14分)已知数列
是等差数列，且
（Ⅰ）求数列的通项公式；
（Ⅱ）令
求数列
前n项和的公式.
22． (14分)如图，在底面是等腰梯形的四棱锥P—ABCD中，PA⊥底面ABCD，AD∥BC，PA=AB=1，BC=2，∠ABC=60º。
①
|
A
D
B
C
23．(14分)已知抛物线
的焦点为F，过
作两条互相垂直的弦
、
，设、的中点分别为
（1）求证：直线
必过定点，并求出定点坐标．
（2）分别以和为直径作圆，求两圆相交弦中点
的轨迹方程．