江苏省四星级高中常州市第二中学
高考数学模拟试卷 2006.1.7
一、选择题(本题每小题5分,共60分)
1.已知集合A={1,2,3,4},集合B={-1,2},设映射![]() :A
:A![]() B,若集合B中的元素都是A中元素的
B,若集合B中的元素都是A中元素的![]() 下的象,那么这样的映射
下的象,那么这样的映射![]() 有
有
A.16个 B.14个 C.12个 D.8个
2.已知角![]() 的终边经过点
的终边经过点![]() ,且
,且![]() ,则
,则![]() 的值是
的值是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]() ( )
( )
3已知椭圆![]() =1的左、右焦点是F1、F2, P 是椭圆上的一点,线段PF1交y轴于点M,若
=1的左、右焦点是F1、F2, P 是椭圆上的一点,线段PF1交y轴于点M,若![]() 是
是![]() 与
与![]() 的等差中项,则
的等差中项,则![]() 等于( )
等于( )
A.3 B. 2 C.5 D.4
4.命题![]() :函数
:函数![]() 不具有奇偶性;命题
不具有奇偶性;命题![]() :当
:当![]() 时,函数
时,函数![]() 为减函数.对于以上两个命题,下列结论中正确的是( )
为减函数.对于以上两个命题,下列结论中正确的是( )
A.命题“![]() 或
或![]() ”为假 B.命题“
”为假 B.命题“![]() 或
或![]() ”为真
”为真
C.命题“![]() 且
且![]() ”为假
D.命题“非
”为假
D.命题“非![]() ”为真
”为真
5.正方体ABCD-A1B1C1D1中,E、F分别为棱AB、C1D1的中点,则直线A1B1与平面A1ECF所成角的正弦为( )
A. B. C. D.
6.点P在直线![]() 上,PA、PB与圆
上,PA、PB与圆![]() 相切于A、B两点,则四边形PAOB面积的最小值为(
)
相切于A、B两点,则四边形PAOB面积的最小值为(
)
A.24 B.16 C.8 D.4
7. 设![]() ,
,![]() 分别是平面直角坐标系内
分别是平面直角坐标系内![]() 轴、
轴、![]() 轴正方向上的两个单位向量,在同一直线上有A、B、C三个点,
轴正方向上的两个单位向量,在同一直线上有A、B、C三个点,![]() ,若
,若![]() ,则实数
,则实数![]() ,
,![]() 的值分别为(
)
的值分别为(
)
A. ![]() 或
或![]() B.
B. ![]() 或
或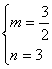
C . ![]() 或
或![]() D.
D. ![]() 或
或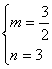
8.以椭圆的右焦点![]() 为圆心作一个圆,使此圆过椭圆中心并交椭圆于点M,N,若过椭圆左焦点
为圆心作一个圆,使此圆过椭圆中心并交椭圆于点M,N,若过椭圆左焦点![]() 的直线MF1是圆
的直线MF1是圆![]() 的切线,则椭圆的离心率为(
)
的切线,则椭圆的离心率为(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9过△ABC的重心任作一直线分别交AB、AC于D、E,![]() 则
则![]() 的值为A.4 B.3
C. 2 D.1
( )
的值为A.4 B.3
C. 2 D.1
( )
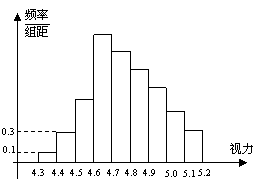 10、为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a, b的值分别为( )
10、为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a, b的值分别为( )
A.0.27, 78 B.0.27, 83
C.2.7, 78 D.2.7, 83
11一个机器猫每秒前进或后退一步,程序设计人员让机器猫以每前进3步,然后再后退2步的规律移动;如果将此机器猫放在数轴的原点上,面向正的方向,以1步的距离为1个单位长,令P(n)表示第n秒时机器猫所在的位置的坐标,且P(0)=0,那么下列结论中错误的是 ( )
A. P(3)=3 B. P(5)=1 C. P(101)=21 D. P(103)<P(104)
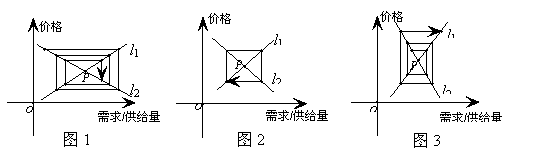 12.经济学中的“蛛网理论”(如图),假定某种商品的“需求—价格”函数的图象为直线l1,“供给—价格”函数的图象为直线l2,它们的斜率分别为k1、k2,l1与l2的交点P为“供给—需求”均衡点,在供求两种力量的相互作用下,该商品的价格和产销量,沿平行于坐标轴的“蛛网”路径,箭头所指方向发展变化,最终能否达于均衡点P,与直线l1、 l2的斜率满足的条件有关,从下列三个图中可知最终能达于均衡点P的条件为
12.经济学中的“蛛网理论”(如图),假定某种商品的“需求—价格”函数的图象为直线l1,“供给—价格”函数的图象为直线l2,它们的斜率分别为k1、k2,l1与l2的交点P为“供给—需求”均衡点,在供求两种力量的相互作用下,该商品的价格和产销量,沿平行于坐标轴的“蛛网”路径,箭头所指方向发展变化,最终能否达于均衡点P,与直线l1、 l2的斜率满足的条件有关,从下列三个图中可知最终能达于均衡点P的条件为
A k1+k2>0 B k1+k2=0 C k1+k2<0 D k1+k2可取任意实数
二、填空题(本题每小题4分,共24分)
13.在△ABC中,已知![]() 的值为
的值为
14.![]() ,若
,若![]() >
>![]() ,则不等式的解集为
,则不等式的解集为
15某校高三年级举行的一次演讲比赛共有10位同学参赛,其中一班有3位,二班有2位,其他班有5位. 若采取抽签的方式确定他们的演讲顺序,则一班的3位同学恰好被排在一起(指演讲序号相连),而二班的2位同学没有被排在一起的概率为
16.已知球面上A、B两点间的球面距离是1,过这两点的球面半径的夹角为60°,则这个球的表面积与球的体积之比是 .
17.把曲线![]() 按向量a=(1,2)平移后得到曲线C2,曲线C2有一条准线方程为x=5,则k的值为 .
按向量a=(1,2)平移后得到曲线C2,曲线C2有一条准线方程为x=5,则k的值为 .
18 定义运算:![]() ,若数列
,若数列![]() 满足
满足 ,且
,且![]() (
(![]() ),则
),则![]() 为 .
为 .
三、解答题(本大题共5小题,共66分。解答应写出文字说明,证明过程或演算步骤):
19.( 本题满分12分) 已知向量![]() 和
和![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
20.(.( 本题满分12分)运动队11月份安排4次体能测试,规定每位运动员一开始就要参加测试,一旦某次测试合格就不必参加以后的测试,否则4次测试都要参加。若李明4次测试当次合格的概率依次组成一公差为![]() 的等差数列,且他直至第二次测试才合格的概率为
的等差数列,且他直至第二次测试才合格的概率为![]()
(1)求李明第一次参加测试就合格的概率P1(结果用分数表示).
(2)求李明11月份体能测试能合格的概率.(结果用分数表示)
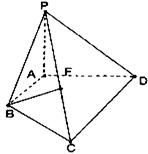 21(本题满分14分)如图已知四棱锥P—ABCD,PA⊥平面ABCD,底面ABCD为直角梯形,∠A=90°且AB//CD,AB=
21(本题满分14分)如图已知四棱锥P—ABCD,PA⊥平面ABCD,底面ABCD为直角梯形,∠A=90°且AB//CD,AB=![]() CD.
CD.
(1)点F在线段PC上运动,且设![]() 为何值时,BF//平面PAD?并证明你的结论;
为何值时,BF//平面PAD?并证明你的结论;
(2)二面角F—CD—B为45°,求二面角B—PC—D的大小;
(3)在(Ⅱ)的条件下,若AD=2,CD=3,求点A到平面PBC的距离.
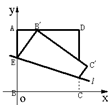
22.(本题满分14分)如图,ABCD是边长为2的正方形纸片,沿某动直线![]() 为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为
为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为![]() ;折痕
;折痕![]() 与AB交于点E,点M满足关系式
与AB交于点E,点M满足关系式![]() 。
。
 (Ⅰ)建立适当的直角坐标系,求点M的轨迹方程;
(Ⅰ)建立适当的直角坐标系,求点M的轨迹方程;
(Ⅱ)若曲线C是由点M的轨迹及其关于边AB对称的曲线组成的,F是边AB上的一点,![]() ,过点F的直线交曲线C于P、Q两点,且
,过点F的直线交曲线C于P、Q两点,且![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
23.(本小题14分,其中第一问 2分,第二问6分,第三问6分)
已知![]() 是定义在R上的函数,其图象交x轴于A,B,C三点,若点B的坐标为(2,0),且
是定义在R上的函数,其图象交x轴于A,B,C三点,若点B的坐标为(2,0),且![]() 在
在![]() 和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
(1)求c的值;
(2)在函数![]() 的图象上是否存在一点M(x0,y0),使得
的图象上是否存在一点M(x0,y0),使得![]() 在点M的切线斜率为3b?若存在,求出点M的坐标;若不存在,说明理由;
在点M的切线斜率为3b?若存在,求出点M的坐标;若不存在,说明理由;
(3)求![]() 的取值范围.
的取值范围.
参考答案
1-6 BADBAC 7-12 CABADA
13 2或-2 14 (0,![]() )
)![]() (
(![]() ) 15
) 15 ![]()
16 ![]() 17 -3 18 38
17 -3 18 38
19: 解:![]() ……………………………………2分
……………………………………2分
![]() ……………………………4分
……………………………4分
= ![]()
=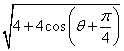 ………………………………………………………7分
………………………………………………………7分
=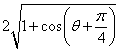 …………………………………………………………10分
…………………………………………………………10分
由已知![]() ,得
,得![]() 又
又![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ……………13分
……………13分
20.解:(1)设四次测试合格的概率依次为![]()
则![]()
∴李明第一次参加测试就合格的概率为![]() ………………6分
………………6分
(2)设A为李明11月份体能测试合格的事件
则![]() …………………………9分
…………………………9分
![]()
∴李明11月体能测试能合格的概率为![]() ……………………12分
……………………12分
21.解:(1)当![]()
证明:取PD中点E,则EF//CD,且![]()
∴四边形ABFE为平行四边形.
∴BF//AE. 又AE![]() 平面PAD ∴BF//平面PAD ……………4分
平面PAD ∴BF//平面PAD ……………4分
(2)![]() 平面ABCD,
平面ABCD,![]() 即是二面角的平
即是二面角的平
面角![]()
![]() 为等腰直角三角形,
为等腰直角三角形,![]()
![]() 平面PCD
又BF//AE,
平面PCD
又BF//AE,![]() 平面PCD.
平面PCD. ![]() 平面PBC,
平面PBC,
∴平面PCD⊥平面PBC,即二面角B—PC—D的大小为90°. ……………8分
(3)在平面PCD内作EH⊥PC于点H,由平面PCD⊥平面PBC且平面PCD![]()
平面PBC=PC知:EH⊥平面PBC.
在![]() ,
,
在![]() 代入得:
代入得:
![]() 即点E到平面PBC的距离为
即点E到平面PBC的距离为![]()
又![]() 点A到平面PBC的距离为
点A到平面PBC的距离为![]() ……14分
……14分
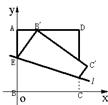 22解答:(1)建立如图所示坐标系,设E(0,t),B’(x0,2),M(x,y),则在
22解答:(1)建立如图所示坐标系,设E(0,t),B’(x0,2),M(x,y),则在![]() 中可求得
中可求得![]() ,∴
,∴![]()
![]()
又![]() ,代入可得:
,代入可得: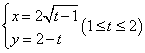
消去t得:![]() (0≤x≤2)(8分)
(0≤x≤2)(8分)
(2)![]() ≤
≤![]() ≤2(14分)
≤2(14分)
23.解:⑴
∵![]() 在
在![]() 和
和![]() 上有相反单调性,
上有相反单调性,
∴ x=0是![]() 的一个极值点,故
的一个极值点,故![]() ,
,
即![]() 有一个解为x=0,∴c=0
……2分
有一个解为x=0,∴c=0
……2分
⑵ ∵![]() 交x轴于点B(2,0)
交x轴于点B(2,0)
∴![]()
令![]() ,则
,则![]()
∵![]() 在
在![]() 和
和![]() 上有相反的单调性
上有相反的单调性
∴![]() , ∴
, ∴![]() ……4分
……4分
假设存在点M(x0,y0),使得![]() 在点M的切线斜率为3b,则
在点M的切线斜率为3b,则![]()
即 ![]()
∵ △=![]() ……6分
……6分
又![]() , ∴△<0
, ∴△<0
∴不存在点M(x0,y0),使得![]() 在点M的切线斜率为3b. ……8分
在点M的切线斜率为3b. ……8分
⑶ 依题意可令
![]()
 ……10分
……10分
![]() ……11分
……11分
∵![]() ,∴当
,∴当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]()
故![]() ……14分
……14分