长郡中学高三第五次月考
数 学 试 卷(理)
时量:120分钟 满分:150分 2006.01.11-12
一、选择题(每题的答案是唯一的。每题5分,共50分):
1、 设f:x→x2是集合A到集合B的映射,若B={1,2},则A∩B等于( )
(A)Φ (B){1} (C)Φ或{2} (D)Φ或{1}
2、
已知关于x的不等式![]() 的解集是[-1,0)则a+b=( )
的解集是[-1,0)则a+b=( )
A.-2 B.-1 C.1 D.3
3、 函数![]() 的图象经过四个象限的充要条件是( )
的图象经过四个象限的充要条件是( )
A、![]() 且
且![]() B、
B、![]() 且
且![]() C、
C、![]() 且
且![]() D、
D、![]()
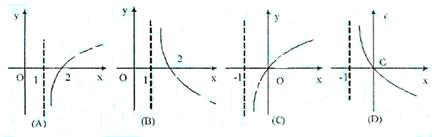
4、
若奇函数![]() 在R上是增函数,那么
在R上是增函数,那么![]() 的大致图像是 ( )
的大致图像是 ( )
5、
若向量![]() ,则数列
,则数列![]() ( )
( )
A、是等差数列不是等比数列 B、是等比数列不是等差数列 C、是等差数列也是等比数列 D、既不是等差数列也不是等比数列
6、 已知平面![]() 、
、![]() 都垂直于平面
都垂直于平面![]() ,且
,且![]() 给出下列四个命题:
给出下列四个命题:
①若![]() ;②若
;②若![]() ;③若
;③若![]() ;④若
;④若![]() . 其中真命题的个数为 ( )
. 其中真命题的个数为 ( )
A.4 B.3 C.2 D.1
7、 若![]() 与
与![]() 的展开式中含有
的展开式中含有![]() 项的系数相等,则实数
项的系数相等,则实数![]() ∈( )
∈( )
(A). ![]() (B)
(B)![]() . (C).
. (C).
![]() (D).
(D).
![]()
8、 △ABC中,角A、B、C所对的边分别为a、b、c,则acosC+ccosA的值为 (
) (A)b. (B)![]() . (C)2cosB. (D)2sinB.
. (C)2cosB. (D)2sinB.
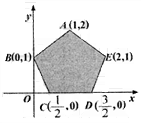
9、 已知以![]() 为自变量的目标函数
为自变量的目标函数![]() 的可行域如图阴影部分(含边界),若使
的可行域如图阴影部分(含边界),若使![]() 取最大值时的最优解有无穷多个,则k的值为( )
取最大值时的最优解有无穷多个,则k的值为( )
A、1 B、2 C、3 D、4
10、 点P在直径为![]() 的球面上,过P作两两垂直的3条弦,若其中一条弦长是另一条弦长的2倍,则这3条弦长之和的最大值是( )
的球面上,过P作两两垂直的3条弦,若其中一条弦长是另一条弦长的2倍,则这3条弦长之和的最大值是( )
A.![]() B.
B.![]() C.
C.![]() D. 6
D. 6
二、填空题(每题4分,共20分)
11、
如果复数![]() 的实部和虚部互为相反数,则b=_______
的实部和虚部互为相反数,则b=_______
12、
已知f ( x )是可导的偶函数,且 ![]() ,则曲线y = f ( x )在(–1,2)处的切线方程是______________
,则曲线y = f ( x )在(–1,2)处的切线方程是______________
13、
由正数组成的等比数列![]() 中,已知
中,已知![]() ,则
,则![]() 等于________
等于________
14、
A和B分别在圆![]() 和双曲线
和双曲线![]() 上运动,则AB的最小值为_____
上运动,则AB的最小值为_____
15、
对于函数![]() ,给出下列四个命题:
,给出下列四个命题:
①存在![]() ;
;
②存在![]() 恒成立;
恒成立;
③存在![]() ,使函数
,使函数![]() 的图像关于y轴对称;
的图像关于y轴对称;
④函数![]() 的图象关于点
的图象关于点![]() 对称;
对称;
其中正确命题的序号是
 高三第五次月考数学试卷(理科)
高三第五次月考数学试卷(理科)
 | |||||
 | |||||


|
数学(理)答案
一、选择:DCDCAABAAB
二、填空:0;y = 4x + 6.;11;![]() ;①③④
;①③④
三、解答:
16、解:(1)∵![]() =(sinB,1-cosB)
, 且与向量
=(sinB,1-cosB)
, 且与向量![]() (2,0)所成角为
(2,0)所成角为![]()
∴![]() ∴tan
∴tan![]() 6’
6’
(2):由(1)可得∴![]() ………8’
………8’
∵![]() ∴
∴![]() ………………10’
………………10’
∴![]() 当且仅当
当且仅当![]() …………………………12’
…………………………12’
17、解:(Ⅰ)当![]() …2分
…2分
两边同除以![]() ,…5分即
,…5分即![]() 成立,
成立,
∴![]() 为首项,d=4为公差的等差数列. …………7分
为首项,d=4为公差的等差数列. …………7分
(Ⅱ)由(Ⅰ)得,![]() ……9分
……9分
∴![]() ………10分设
………10分设![]() 是数列
是数列![]() 的第t项,则
的第t项,则![]() 解得,t=11∈N*,………13分∴
解得,t=11∈N*,………13分∴![]() 是数列
是数列![]() 的第11项.…………14分
的第11项.…………14分
18、解:(1)A中2张钱币取1张,有2种情况, B中3张钱币取1张,有3种情况, ∴互换一次有2´3 = 6种情况, 其中10元币恰是一张的情况有3种, ∴A袋中10元钱币恰是一张的概率为P1
=![]() .
.
(2)列表:
| ξ | 10元 | 15元 | 20元 |
| P |
|
|
|
Eξ= ![]() ´10 +
´10 + ![]() ´15 +
´15 + ![]() ´20 =
´20 = ![]() .答略
.答略
19、解法一:(1)∵PB⊥底面ABCD,CD⊥PD,∴CD⊥BD.在直角梯形
ABCD中,AB=AD=3,∴BC=6.取BC的中点F,连结PF,则AF∥CD.
∴异面直线PA和CD所成的角就是PA和AF所成的角∠PAF 在Δ
![]() PAF中,AF=PA=PF= ∴∠PAF=60°.
PAF中,AF=PA=PF= ∴∠PAF=60°.![]()
(2)连结AC交BD于G,连结EG,
PC∥EG.又EG平面EBD,PC平面EBD ∴PC∥平面EBD.
![]() (3)∵PB⊥平面ABCD,∴AD⊥PB.又∵AD⊥AB,∴AD⊥平面EAB.作AH⊥BE,垂足为H,连结DH,则DH⊥BE,∴∠AHD是二面角A—BE—D的平面角.在ΔABE中,BE=
(3)∵PB⊥平面ABCD,∴AD⊥PB.又∵AD⊥AB,∴AD⊥平面EAB.作AH⊥BE,垂足为H,连结DH,则DH⊥BE,∴∠AHD是二面角A—BE—D的平面角.在ΔABE中,BE=
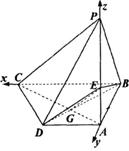 解法二:(1)建立如图所示的直角坐标系B—xyz.设BC=a,则A(0,3,0),
解法二:(1)建立如图所示的直角坐标系B—xyz.设BC=a,则A(0,3,0),
![]() P(0,0,3),D(3,3,0)
C(a,0,0),
P(0,0,3),D(3,3,0)
C(a,0,0),

20、解:(Ⅰ)设P点的坐标为(x,y),则![]() ,
,![]() ,
,
又![]() ,故
,故![]() ,
,![]() . 由题知向量
. 由题知向量![]() 与向量
与向量![]() 平行,故
平行,故![]() (y + a) = ax. 又向量
(y + a) = ax. 又向量![]() 与向量
与向量![]() 平行,故y – a = 2
平行,故y – a = 2![]() . 两方程联立消去参数
. 两方程联立消去参数![]() ,得点P (x,y)的轨迹方程是 (y + a)(y
– a) = 2a2x2,即y2 – a2 = 2a2x2. (6分)
,得点P (x,y)的轨迹方程是 (y + a)(y
– a) = 2a2x2,即y2 – a2 = 2a2x2. (6分)
(Ⅱ)∵![]() ,故点P的轨迹方程为2y2 – 2x2
= 1,
,故点P的轨迹方程为2y2 – 2x2
= 1,
此时点E (0,1)为双曲线的焦点. ①若直线l的斜率不存在,其方程为x = 0,l与双曲线交于![]() 、
、![]() ,此时
,此时![]() . (8分)
. (8分)
②若直线l的斜率存在,设其方程为y = kx + 1,代入2y2 – 2x2 = 1化简得 2(k2 – 1) x2 + 4kx + 1 = 0.∴直线l与双曲线交于两点,
∴△=
(4k)2 – 8 (k2 – 1) > 0且k2 – 1≠0.解得k≠±1.设两交点为M (x1,y1)、N (x2,y2),则x1 + x2 =![]() ,x1x2 =
,x1x2 =![]() . (10分)
. (10分)
此时![]() = x1x2 + k2x1x2
= (k2 + 1) x1x2 =
= x1x2 + k2x1x2
= (k2 + 1) x1x2 =![]() .
.
当– 1 < k < 1时,k2 – 1 < 0,故![]() ≤
≤![]() ;
;
当k > 1或k < – 1时,k2 – 1 > 0,故![]() .
.
综上所述,![]() 的取值范围是
的取值范围是![]() ∪
∪![]() . (14分)
. (14分)
21、(1)解:
∵![]() 且
且![]() ∴
∴![]() ,
,![]()
∵![]() 且
且![]() ∴
∴![]()
∵![]() 且
且![]() ∴
∴![]() …………………………
…………………………
![]() 且
且![]() ∴
∴![]()
于是![]()
(2)证明: ![]() <3
<3
(3)证明: ∵![]()
当![]() ≥4时,
≥4时,![]() =
=![]()
∴![]()