2006届 高三联考试卷
高三联考试卷
(2006.1)
数 学
考试时间:120分钟 满分:150分
第Ⅰ卷(选择题 共60分)
一、选择题(每小题5分,共10小题,共50分),把答案涂在答题卡上.
1.
圆![]() 与圆
与圆![]() 关于直线
关于直线![]() 对称,则
对称,则![]() 与
与![]() 的值分别等于( )
的值分别等于( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
2.
等差数列![]() 的通项公式是
的通项公式是![]() ,其前
,其前![]() 项和为
项和为![]() ,则数列
,则数列![]() 的前10项和为 ( )
的前10项和为 ( )
A.75 B.70 C.120 D.100
3.
先将![]() 的图象沿
的图象沿![]() 轴向右平移
轴向右平移![]() 个单位,再将图象上每一个点的横坐标伸长为原来的2倍,而保持它们的纵坐标不变,得到的曲线与
个单位,再将图象上每一个点的横坐标伸长为原来的2倍,而保持它们的纵坐标不变,得到的曲线与![]() 的图象相同,则
的图象相同,则![]() 是( )
是( )
A.![]() B.
B. ![]()
C.![]() D.
D.![]()
4.
已知直线![]() 、
、![]() 和平面
和平面![]() ,则
,则![]() 的一个必要不充分条件是( )
的一个必要不充分条件是( )
A. ![]() ,
,![]() B.
B.![]() ,
,![]()
C. ![]() ,
,![]() D.
D.![]() 、
、![]() 与
与![]() 成等角
成等角
5.
函数![]() 在其定义域上单调递减,且值域为
在其定义域上单调递减,且值域为![]() ,则它的反函数的值域是( )
,则它的反函数的值域是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.
函数![]() 满足:
满足:![]() ,则下列结论正确的是(
)
,则下列结论正确的是(
)
A.![]() 的图象关于直线
的图象关于直线![]() 对称 B.
对称 B.![]() 的图象关于点(1,0)对称
的图象关于点(1,0)对称
C.函数![]() 是奇函数 D.函数
是奇函数 D.函数![]() 周期函数
周期函数
7.
无穷数列![]() 中,
中,![]() ,其前
,其前![]() 项和为
项和为![]() .当
.当![]() ,
,![]() 时,
时,![]() ,则
,则![]() 等于(
)
等于(
)
A.0 B.![]() C.
C.![]() D.3
D.3
8.
已知![]() ,全集U=R,集合M=
,全集U=R,集合M=![]() ,N=
,N=![]() ,P=
,P=![]() ,则P与M、N的关系为 ( )
,则P与M、N的关系为 ( )
A.P= (CUM) ![]() N B.P=M
N B.P=M![]() (CUN) C.P=M
(CUN) C.P=M![]() N D.P=M
N D.P=M![]() N
N
9.
![]() 为三角形的一个内角,且
为三角形的一个内角,且![]() ,则
,则![]() 与
与![]() 的值依次为
( )
的值依次为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.
已知椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() 和
和![]() .若
.若![]() 是
是![]() 与
与![]() 的等比中项,
的等比中项,![]() 是
是![]() 与
与![]() 的等差中项,则椭圆的离心率等于( )
的等差中项,则椭圆的离心率等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题 共100分)
二.填空题:(本大题共4小题;每小题5分,共20分)
11.
不等式![]() 对所有
对所有![]() 都成立,则
都成立,则![]() 的取值范围是
.
的取值范围是
.
12.
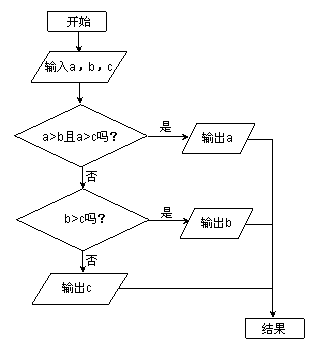 右图所示的流程图是将一系列指令和问题用框图的形式排列而成,箭头说明下一步是到哪一个框图。阅读这个流程图,回答下列问题:
右图所示的流程图是将一系列指令和问题用框图的形式排列而成,箭头说明下一步是到哪一个框图。阅读这个流程图,回答下列问题:
若a<b<c,则输出的数是 ;(2分)
若a=![]() ,b=
,b=![]() ,c=
,c=![]() ,则输出的数是
.(用字母a、b、c填空)(3分)
,则输出的数是
.(用字母a、b、c填空)(3分)
13.
点A、B、C是表面积为![]() 的球O表面上的三点,且每两点间的球面距离都等于
的球O表面上的三点,且每两点间的球面距离都等于![]() ,则三棱锥O–ABC的体积等于
.
,则三棱锥O–ABC的体积等于
.
14. 有下列四个命题:
①函数![]() 的值域是
的值域是![]() ;
;
②平面内的动点P到点F![]() 和到直线
和到直线![]() :
:![]() 的距离相等,则P的轨迹是抛物线;
的距离相等,则P的轨迹是抛物线;
③直线AB与平面![]() 相交于点B,且AB与
相交于点B,且AB与![]() 内相交于C的三条互不重合的直线CD、CE、CF所成的角相等,则AB
内相交于C的三条互不重合的直线CD、CE、CF所成的角相等,则AB![]() ;
;
④函数![]() 的最小正周期是
的最小正周期是![]() .
.
其中正确的命题的编号是 .
2006届
|
 高三联考试卷
高三联考试卷
(2006.1)
数学答卷
一、选择题(5![]() 10=50)
10=50)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题(5![]() 4=20)
4=20)
11. 12. (2分) (3分)
13. 14.
三、解答题:(共6小题,共80分)
15. (12分)在△ABC中,内角A、B、C的对边分别为![]() 、
、![]() 、
、![]() .其中
.其中![]() ,
,![]() .
.
(1)求角B的大小;
(2)求![]() +
+![]() 的取值范围.
的取值范围.
16.
(13分)设![]() ,函数
,函数![]() 是奇函数.
是奇函数.
(1)求常数![]() 的值;
的值;
(2)实数![]() ,
,![]() 是函数
是函数![]() 的反函数,解关于
的反函数,解关于![]() 的不等式
的不等式
![]() .
.
17. (13分)我国是水资源比较贫乏的国家之一,各地采用了价格调控等手段来达到节约用水的目的.某市用水收费的方法是:水费=基本费 + 超额费 + 定额损耗费.
若每月用水量不超过最低限量![]() 时,只付基本费8元和每月的定额损耗费
时,只付基本费8元和每月的定额损耗费![]() 元;若用水量超过
元;若用水量超过![]() 时,除了付同上的基本费和定额损耗费外,超过部分每1
时,除了付同上的基本费和定额损耗费外,超过部分每1![]() 付
付![]() 元的超额费.已知每户每月的定额损耗费不超过5元.
元的超额费.已知每户每月的定额损耗费不超过5元.
该市一家庭今年一季度的用水量和支付费用见下表,根据表中的数据求![]() 、
、![]() 、
、![]() .
.
| 月份 | 用水量( | 水费(元) |
| 1 | 9 | 9 |
| 2 | 15 | 19 |
| 3 | 22 | 33 |
18. (14分)如图,棱柱ABCD–A1B1C1D1的所有棱长都等于2,∠ABC=![]() ,
,
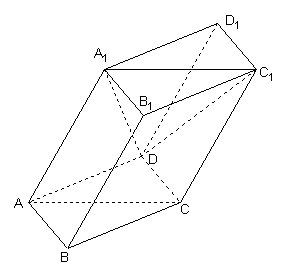 平面A A1C1C⊥平面ABCD,∠A1AC=
平面A A1C1C⊥平面ABCD,∠A1AC=![]() .
.
(1) 求二面角D–A1A–C的大小;
(2) 求点B1到平面A1ADD1的距离;
(3) 在直线CC1上是否存在点P,使BP // 平面DA1C1?若存在,求出点P的位置;若不存在,说明理由.
19.
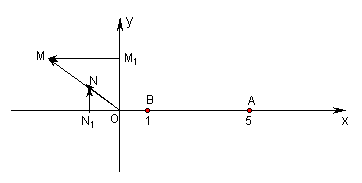
(14分)在直角坐标平面上,O为原点,M为动点,![]() ,
,![]() .过点M作MM1⊥
.过点M作MM1⊥![]() 轴于M1,过N作NN1⊥
轴于M1,过N作NN1⊥![]() 轴于点N1,
轴于点N1,![]() .记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线
.记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线![]() 交曲线C于两个不同的点P、Q(点Q在A与P之间).
交曲线C于两个不同的点P、Q(点Q在A与P之间).
(Ⅰ)求曲线C的方程;
(Ⅱ)证明不存在直线![]() ,使得
,使得![]() ;
;
 (Ⅲ)过点P作
(Ⅲ)过点P作![]() 轴的平行线与曲线C的另一交点为S,若
轴的平行线与曲线C的另一交点为S,若![]() ,证明
,证明![]() .
.
20.
(14分)数列![]() 的各项均为正值,
的各项均为正值,![]() ,对任意
,对任意![]() ,
,![]() ,
,![]() 都成立.
都成立.
(Ⅰ)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(Ⅱ)当![]() 且
且![]() 时,证明对任意
时,证明对任意![]() 都有
都有![]() 成立.
成立.
2006届
|
 高三联考试卷
高三联考试卷
(2006.1)数学答案、评分说明
一、选择题(5![]() 10=50)
10=50)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| B | A | C | D | C | D | A | B | C | B |
二、填空题(5![]() 4=20)
4=20)
11. ![]() 12.
c (2分) b (3分)
12.
c (2分) b (3分)
13. ![]() 14.
③、④
14.
③、④
三、解答题:(共6小题,共80分)
15.(12分)在△ABC中,内角A、B、C的对边分别为![]() 、
、![]() 、
、![]() .其中
.其中![]() ,
,![]() .
.
(1)求角B的大小;
(2)求![]() +
+![]() 的取值范围.
的取值范围.
解:(1)由![]() 得
得
![]() 1分
1分
可知![]() ,否则有,
,否则有,![]() ,
,![]() ,互相矛盾.
2分
,互相矛盾.
2分
∴ ![]() ,即
,即![]() 3分
3分
而![]() ,所以
,所以![]() .
4分
.
4分
∴ B=![]() .
5分
.
5分
(2)由正弦定理有,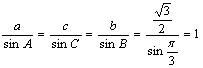 ,
,
∴ ![]() ,
, ![]() ,
7分
,
7分
∴![]() 9分
9分
∵ ![]() , ∴
, ∴ ![]() ,
于是
,
于是![]() , 11分
, 11分
则![]() +
+![]() 的取值范围是
的取值范围是![]() .
12分
.
12分
16.(13分)设![]() ,函数
,函数![]() 是奇函数.
是奇函数.
(1)求常数![]() 的值;
的值;
(2)实数![]() ,
,![]() 是函数
是函数![]() 的反函数,解关于
的反函数,解关于![]() 的不等式
的不等式
![]() .
.
解:(1)![]() 为奇函数的充要条件是:对任意
为奇函数的充要条件是:对任意![]() ,
,![]() 都成立. 1分
都成立. 1分
![]() 4分
4分
即![]() 恒成立,
恒成立,
∴ ![]() 5分
5分
(2)
函数![]() 的定义域是R.
的定义域是R.
![]() 可得
可得![]() 的值域为
的值域为![]() .
6分
.
6分
由![]() 得,
得, ![]() ,从而得到
,从而得到![]() 8分
8分
则原不等式为 ![]()
由![]() 及函数
及函数![]() 单调递增知,不等式等价于
单调递增知,不等式等价于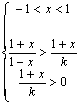
![]() 10分
10分
当![]() 时,原不等式的解集为
时,原不等式的解集为![]() ;
11分
;
11分
当![]() 时,原不等式的解集为
时,原不等式的解集为![]() .
13分
.
13分
17.(13分)我国是水资源比较贫乏的国家之一,各地采用了价格调控等手段来达到节约用水的目的.某市用水收费的方法是:水费=基本费 + 超额费 + 定额损耗费.
若每月用水量不超过最低限量![]() 时,只付基本费8元和每月的定额损耗费
时,只付基本费8元和每月的定额损耗费![]() 元;若用水量超过
元;若用水量超过![]() 时,除了付同上的基本费和定额损耗费外,超过部分每1
时,除了付同上的基本费和定额损耗费外,超过部分每1![]() 付
付![]() 元的超额费.已知每户每月的定额损耗费不超过5元.
元的超额费.已知每户每月的定额损耗费不超过5元.
该市一家庭今年一季度的用水量和支付费用见下表,根据表中的数据求![]() 、
、![]() 、
、![]() .
.
| 月份 | 用水量( | 水费(元) |
| 1 | 9 | 9 |
| 2 | 15 | 19 |
| 3 | 22 | 33 |
解:设月用水量为![]()
![]() ,当月支付费用为
,当月支付费用为![]() 元,则
元,则
![]() 3分
3分
由题知,![]()
![]() 4分
4分
从表中知,2月、3月的费用均大于13元,故用水量15![]() 、22
、22![]() 均大于最低限量
均大于最低限量![]() ,将
,将![]() 、
、![]() 分别代入上述(2)可得
分别代入上述(2)可得
![]() 解得
解得![]() 6分
6分
![]() (3)
7分
(3)
7分
若1月份用水量9![]() 超过最低限量
超过最低限量![]() ,即
,即![]() ,将
,将![]() 代入上述(2)式中得
代入上述(2)式中得
![]() 得
得![]() ,这与(3)式矛盾.
,这与(3)式矛盾.
![]() ,
10分
,
10分
因此1月份的付款应为:![]()
![]() 11分
11分
故![]() 12分
12分
答:略. 13分
18. (14分)如图,棱柱ABCD–A1B1C1D1的所有棱长都等于2,∠ABC=![]() ,
,
平面A A1C1C⊥平面ABCD,∠A1AC=![]() .
.
(4) 求二面角D–A1A–C的大小;
(5) 求点B1到平面A1ADD1的距离;
(6)  在直线CC1上是否存在点P,使BP // 平面DA1C1?若存在,求出点P的位置;若不存在,说明理由.
在直线CC1上是否存在点P,使BP // 平面DA1C1?若存在,求出点P的位置;若不存在,说明理由.
解:(1)在平面ABCD上,AB=BC=CD=DA=2
∴四边形ABCD为菱形
∴BD⊥AC
∵平面A A1C1C⊥平面ABCD
∴BD⊥平面A A1C1C
设AC∩BD=O,过O作OE⊥AA1于E点,连结DE,由三垂线定理有,AA1⊥DE,
则∠DEO为二面角D–A1A–C的平面角 2分
在菱形ABCD中,AB=2, ∠ABC=![]()
∴AC=AB=BC=2
∴AO=1, DO=![]()
在Rt△AEO中,
![]()
在Rt△DEO中,
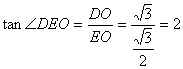
∴∠DEO=![]() 4分
4分
∴二面角D–A1A–C的大小为![]() .
5分
.
5分
(2)连结A1O、A1B.由于B1B //平面A1A DD1,所以B、B1到平面A1A DD1的距离相等,设点B到平面A1A DD1的距离等于![]() .
6分
.
6分
在△AA1
O中,![]()
∴![]() ∴A1O⊥AO
∴A1O⊥AO
而平面A A1C1C⊥平面ABCD ∴A1O⊥平面ABCD 7分
由上述第(1)问有,ED ⊥A1A1且![]()
∴![]()
又![]()
由![]() 有,
有,![]() 9分
9分
∴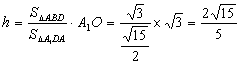
即点B1到平面A1ADD1的距离等于![]() .
10分
.
10分
(3)存在这样的点P. 连结B1C.
∵A1B1![]() AB
AB![]() DC ∴四边形A1B1CD为平行四边形 ∴A1D//B1C 12分
DC ∴四边形A1B1CD为平行四边形 ∴A1D//B1C 12分
在C1C的延长线上取点P,使C1C=CP,连结BP,
因B1B![]() C1C ∴B1B
C1C ∴B1B![]() CP ∴四边形BB1CP为平行四边形
CP ∴四边形BB1CP为平行四边形
∴BP//B1C ∴BP//A1D 13分
则有BP // 平面DA1C1 14分
注:本题的侧棱长为2是一个多余的条件,其作为已知可以减少向量坐标解法的运算量。
19.(14分)在直角坐标平面上,O为原点,M为动点,![]() ,
,![]() .过点M作MM1⊥
.过点M作MM1⊥![]() 轴于M1,过N作NN1⊥
轴于M1,过N作NN1⊥![]() 轴于点N1,
轴于点N1,![]() .记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线
.记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线![]() 交曲线C于两个不同的点P、Q(点Q在A与P之间).
交曲线C于两个不同的点P、Q(点Q在A与P之间).
(1) 求曲线C的方程;
(2)
证明不存在直线![]() ,使得
,使得![]() ;
;
(3)
 过点P作
过点P作![]() 轴的平行线与曲线C的另一交点为S,若
轴的平行线与曲线C的另一交点为S,若![]() ,证明
,证明![]() .
.
(1)解:设点T的坐标为![]() ,点M的坐标为
,点M的坐标为![]() ,则M1的坐标为
,则M1的坐标为![]()
![]() ∴点N的坐标为
∴点N的坐标为![]() 1分
1分
∴N1的坐标为![]() ∴
∴![]() 2分
2分
由![]() 有
有 ![]()
∴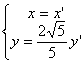 由此得
由此得![]() 3分
3分
由![]() 有
有![]()
∴![]() 即
即![]() ,即为所求的方程.曲线C为椭圆. 4分
,即为所求的方程.曲线C为椭圆. 4分
(2)证:点A(5,0)在曲线C即椭圆的外部,当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 与椭圆C无交点,所以直线
与椭圆C无交点,所以直线![]() 斜率存在,并设为
斜率存在,并设为![]() .直线
.直线![]() 的方程为
的方程为![]() . 5分
. 5分
由方程组 得
得![]() 6分
6分
依题意![]() ,得
,得![]() .
7分
.
7分
当![]() 时,设交点
时,设交点![]() ,PQ的中点为R
,PQ的中点为R![]() ,则
,则
![]() ,
,
![]()
∴![]() 8分
8分
又![]()
![]() BR⊥
BR⊥![]()
![]()
![]()
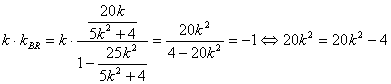 9分
9分
但![]() 不可能成立,所以不存在直线
不可能成立,所以不存在直线![]() 使得
使得![]() .
10分
.
10分
(3)证明:由题有S![]() ,
,![]() .
.
则有方程组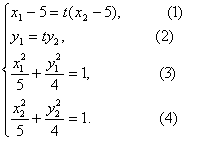 11分
11分
由(1)得:![]()
将(2)、(5)代入(3)有![]()
整理并将(4)、(5)代入得 ![]()
易知![]() ,解得
,解得![]() 12分
12分
因![]() ,故
,故![]() ,
,![]() ,
,
∴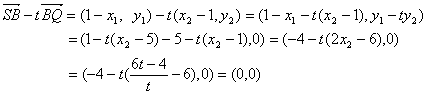
∴![]() .
14分
.
14分
20.(14分)数列![]() 的各项均为正值,
的各项均为正值,![]() ,对任意
,对任意![]() ,
,![]() ,
,![]() 都成立.
都成立.
(1)
求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)
当![]() 且
且![]() 时,证明对任意
时,证明对任意![]() 都有
都有![]() 成立.
成立.
(1)
解:由![]() 得,
得,
![]() 2分
2分
数列![]() 的各项为正值,
的各项为正值,![]()
∴![]() 3分
3分
∴![]() 4分
4分
又![]()
∴数列![]() 为等比数列.
6分
为等比数列.
6分
∴![]() ,
,
![]() ,即为数列
,即为数列![]() 的通项公式. 7分
的通项公式. 7分
![]() 8分
8分
(2)设![]()
∴![]() (1) 10分
(1) 10分
当![]() 时,
时,![]() ,
,![]()
∴![]()
∴![]() , 当且仅当
, 当且仅当![]() 时等号成立.
12分
时等号成立.
12分
上述(1)式中,![]() ,
,![]() ,
,![]() 全为正,所以
全为正,所以
![]() 13分
13分
∴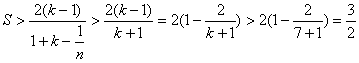 14分
14分
得证.