2006届城中高三第一次测试(数学卷)
(满分150分,考试时间120分钟)
第I卷(选择题 共50分)
一、选择题:(本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若集合![]() ,
,![]() ,那么
,那么![]() ( )
( )
![]() .
.![]()
![]() .
.![]()
![]() .
.![]()
![]() .
.![]()
2.已知等比数列的公比是2,且前四项的和为1,那么前八项的和为
( )
A.15 B.17 C.19 D.21
3.条件P:![]() 条件q:
条件q:![]() 则p是q的( )
则p是q的( )
![]() .充分不必要条件
.充分不必要条件
![]() .必要不充分条件
.必要不充分条件
![]() .充要条件
.充要条件 ![]() .既不充分也不必要条件
.既不充分也不必要条件
4.函数![]() 的定义域是( )
的定义域是( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
5. 函数![]() 的值域是( )
的值域是( )
A.![]() B.
B.![]() C. (0,1) D.
C. (0,1) D.![]()
6. ![]() 的图象大致是 ( )
的图象大致是 ( )
|
A B C D
7.已知函数f(x)=![]() +2的定义域为(0,3],则它的反函数
+2的定义域为(0,3],则它的反函数![]() 的定义域为 ( )
的定义域为 ( )
A.[-1,1] B.(-∞,1] C.[1,+∞) D.[3,+∞)
8.已知函数![]() 在区间
在区间![]() 上是增函数,则实数
上是增函数,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.设![]() 是等差数列,从
是等差数列,从![]() 中任取3个不同的数,使这三个数仍成等差数列,则这样不同的等差数列最多有 ( )
中任取3个不同的数,使这三个数仍成等差数列,则这样不同的等差数列最多有 ( )
A.90个 B.120个 C.180个 D.200个
10.已知定义在R上的函数y=f (x)满足以下三个条件:①对于任意的x![]() R,都有
R,都有![]() ;②对于任意的
;②对于任意的![]() ,且
,且![]() ,都有f (x1)<f (x2);
,都有f (x1)<f (x2);
③函数y=f (x+2)的图象关于y轴对称。则下列结论中正确的是 ( )
(A)f (4.5)<f (7)<f (6.5) (B)f (7)<f (4.5)<f (6.5)
(C)f (7)<f (6.5)<f (4.5) (D)f (4.5)<f (6.5)<f (7)
二、填空题:(本大题共4小题,每小题5分,共20分)
11.已知等差数列![]() 中,
中,![]() 的值是__________
的值是__________
12.定义在![]() 上的偶函数
上的偶函数![]() ,
,![]() 是增区间,则不等式
是增区间,则不等式![]() 的
的
解集是
13.若函数![]() 是奇函数,则a=
.
是奇函数,则a=
.
14.把下面不完整的命题补充完整,并使之成为真命题.
若函数![]() 的图象与
的图象与![]() 的图象关于
对称,则函数
的图象关于
对称,则函数![]() =
=
__(注:填上你认为可以成为真命题的一种情形即可,不必考虑所有可能的情形)
2006届城中高三第一次测试(数学卷)
第![]()
![]() 卷(共100分)
卷(共100分)
班级_____ 姓名_____ 总分_____
一、选择题:(本大题共12小题,每小题5分,共50分.)
| 题目 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题:11._____________ 12.____________
13._____________ 14.____________ _____________
三、解答题(本大题有6小题,共80分)
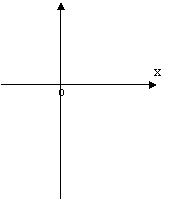
15. (本小题满分13分)已知二次函数f(x)的图象过(-1,0),(3,0),(1,-8)。
(1) 求f(x)的解析式
(2) 画f(x)的图象,并由图象给出该函数的值域
(3) 求不等式f(x)≥0的解集
|
16.(本小题满分13分)设数列![]() 的前n项和为Sn=2n2,
的前n项和为Sn=2n2,![]() 为等比数列,且
为等比数列,且![]()
(Ⅰ)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,求数列
,求数列![]() 的前n项和Tn.
的前n项和Tn.
17.(本小题满分13分)已知![]() ,
,![]() ,若
,若![]() ,求实数
,求实数![]() 的取值范围
的取值范围
18.(本小题满分13分)
学校餐厅每天供应1000名学生用餐,每星期一有A、B两样菜可供选择,调查资料表明,凡是在本周星期一选A菜的,下周星期一会有20%改选B,而选B菜的,下周星期一则有30%改选A,若用A![]() 、B
、B![]() 分别表示在第n个星期一选A、B菜的人数。
分别表示在第n个星期一选A、B菜的人数。
(1)试以A![]() 表示A
表示A![]() ;(2)若A
;(2)若A![]() =200,求{A
=200,求{A![]() }的通项公式;
}的通项公式;
(3)问第n个星期一时,选A与选B的人数相等?
19.(本小题满分14分)
已知数列![]() 满足
满足![]()
(Ⅰ)求证:数列![]() 为等差数列;
为等差数列;
(Ⅱ)试问![]() 是否是数列
是否是数列![]() 中的项?如果是,是第几项;如果不是,请说明理由.
中的项?如果是,是第几项;如果不是,请说明理由.
20.(本小题满分14分)设函数f(x)的定义域是R,对于任意实数m,n,恒有f(m+n)=f(m)f(n),且当x>0时,0<f(x)<1。
⑴求证:f(0)=1,且当x<0时,有f(x)>1;
⑵判断f(x)在R上的单调性;
⑶设集合A={(x,y)f(x2)f(y2)>f(1)},集合B={(x,y)f(ax-y+2)=1,a∈R},若A∩B=![]() ,求a的取值范围。
,求a的取值范围。
2006届城中第一次测试数学卷参考答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | B | A | D | C | D | C | B | C | A |
二、填空题
11、 15 12、![]() 13、
13、![]()
14、(本题有多个答案)①x轴,![]() ②y轴,
②y轴,![]() )
)
③原点,![]() ④
④![]() ,
, ![]()
15.解:(1)![]() ,经过图象(1,-8),得
,经过图象(1,-8),得
![]() ,解得a=2……………………3分
,解得a=2……………………3分
![]()
![]() …………4分
…………4分
(2)图略 值域:![]() …………7分
…………7分
(3)解集:![]() …………10分
…………10分
(4)![]()
![]() ……13分
……13分
16.解:(1):当![]() …………1分
…………1分
![]() …………3分
…………3分
故{an}的通项公式为![]() 的等差数列. ………4分
的等差数列. ………4分
设{bn}的公比为![]() …………5分
…………5分
故![]() …………6分
…………6分
(II)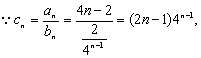
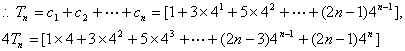 …………9分
…………9分
两式相减得
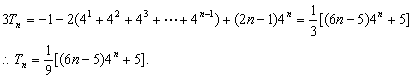 …………13分
…………13分
17.解:在A中:![]() 则
则![]() …………4分
…………4分
在B中:![]() 又因为
又因为![]() 所以
所以![]() …………8分
…………8分
∵![]() ∴
∴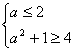 解得:
解得:![]() …………13分
…………13分
18.(1)依题意,得
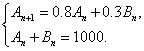 ① …………2分
① …………2分
将B![]() =1000-A
=1000-A![]() 代入①,得A
代入①,得A![]() =0.5A
=0.5A![]() +300 ②…………4分
+300 ②…………4分
(2)设A![]() +
+![]() =0.5(A
=0.5(A![]() +
+![]() ),即A
),即A![]() =0.5A
=0.5A![]() -0.5
-0.5![]() ,
,
得-0.5![]() =300,
=300, ![]()
![]() =-600. ………7分
=-600. ………7分
![]() { A
{ A![]() -600}是以A
-600}是以A![]() -600=200-600=-400为首项,公比为0.5的等比数列。
-600=200-600=-400为首项,公比为0.5的等比数列。
![]() A
A![]() -600=-400×0.5
-600=-400×0.5![]() ,
,![]() A
A![]() =600-400×0.5
=600-400×0.5![]() 。…………9分
。…………9分
(3)![]() A
A![]() = B
= B![]() ,且A
,且A![]() + B
+ B![]() =1000,
=1000,![]() A
A![]() =500,得600-400×0.5
=500,得600-400×0.5![]() =500。
=500。![]() 0.5
0.5![]() =0.5
=0.5![]() ,n-1=2
,n-1=2![]() n=3。即第三个星期一时,选A菜与选B菜的人数相等…13分
n=3。即第三个星期一时,选A菜与选B菜的人数相等…13分
19.解(Ⅰ)当![]() …………3分
…………3分
两边同除以![]() ,…………5分
,…………5分
即![]() 成立,
成立,
∴![]() 为首项,d=4为公差的等差数列. …………7分
为首项,d=4为公差的等差数列. …………7分
(Ⅱ)由(Ⅰ)得,![]() ……9分
……9分
∴![]() …………11分
…………11分
设![]() 是数列
是数列![]() 的第t项,则
的第t项,则![]()
解得,t=11∈N*,………13分
∴![]() 是数列
是数列![]() 的第11项.…………14分
的第11项.…………14分
20.解:⑴f(m+n)=f(m)f(n),令m=1,n=0,
则f(1)=f(1)f(0),且由x>0时,0<f(x)<1,∴f(0)=1;…………2分
设m=x<0,n=-x>0,∴f(0)=f(x)f(-x),∴f(x)=![]() >1。…………4分
>1。…………4分
⑵设x1<x2,则x2-x1>0,∴0<f(x2-x1)<1,
∴f(x2)-f(x1)=f[(x2-x1)+x1]-f(x1)=f(x2-x1)f(x1)-f(x1)=f(x1)[f(x2-x1)-1]<0,
∴f(x)在R上单调递减。…………8分
⑶∵f(x2)f(y2)>f(1),∴f(x2+y2)>f(1),…………9分
由f(x)单调性知x2+y2<1,又f(ax-y+2)=1=f(0),∴ax-y+2=0,…………11分
又A∩B=![]() ,∴
,∴![]() ,∴a2+1≤4,从而
,∴a2+1≤4,从而![]() ……14分
……14分