河北省唐山一中2005—2006学年度高三年级摸底考试
数学(理科)
YCY
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,满分150分.
第Ⅰ卷(选择题共50分)
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中有且只有一项是符合题目要求的.
1.抛物线![]() 在点P(-1,1)处的切线与直线3x-y+1=0的夹角是 ( )
在点P(-1,1)处的切线与直线3x-y+1=0的夹角是 ( )
A.30° B.45° C.60° D.90°
2.![]() 的值为 ( )
的值为 ( )
A.0 B.![]() C.1 D. 2
C.1 D. 2
3.在![]() 的展开式中,
的展开式中,![]() 的系数是 ( )
的系数是 ( )
A.6 B.12 C.18 D.24
4.设复数![]() ,若z为纯虚数,则a的值为 ( )
,若z为纯虚数,则a的值为 ( )
A.-8 B.-5 C.-4 D.-1
5.已知函数 在区间(-∞,1
在区间(-∞,1![]() 内是连续函数,则a的值为
内是连续函数,则a的值为
( )
A.2 B.1 C.![]() D.
D.![]()
6.高三某班有学生50人,其中男生30人,女生20人,为了调查这50名学生的身体状况,
现采用分层抽样的方法,抽取一个容量为20的样本,则该班某男生甲被抽中的概率为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.某机器生产的螺栓长度ξ服从正态分布N(10.05,0.062)(单位:cm),规定螺栓长度在
10.05±0.12(cm)范围内为合格品,则该机器生产的螺栓中,任取一个螺栓为合格品
的概率是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.省博物馆在下周内要接待师大附中等三所学校的学生参观,每天只安排一所学校,双休
日不安排,其中由于师大附中学生人数多,要连续参观两天,其余两学校各参观一天,
则不同的安排方案共有 ( )
A.12种 B.24种 C.48种 D.60种
9.在钝角△ABC中,已知AB=![]() ,AC=1,∠B=30°,则△ABC的面积等于 ( )
,AC=1,∠B=30°,则△ABC的面积等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
|
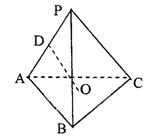
③OD⊥BC; ④PA=2OD.
其中正确结论的个数共有( )
A.1个 B.2个
C.3个 D.4个
第Ⅱ卷(非选择题共100分)
二、填空题:本大题共5小题,每小题4分,共20分,请把各题的正确答案填写在题中的
11.不等式![]() 的解集是
.
的解集是
.
|
球面上,则该球的表面积为 .
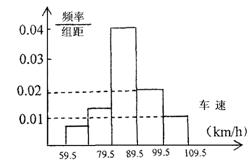
13.在某路段车辆检测点,对200辆汽车
的车速进行检测,检测结果表示为如
右频率分布直方图,则车速不小于
90km/h的汽车约有 辆.
14.已知两定点M(0,3),N(0,-3),若某曲线上存在点P,使PM-PN=4,则称该曲
线为“C型曲线”,给出下列曲线方程:①![]() ;②y=x;③y2=4x;④
;②y=x;③y2=4x;④![]()
其中是“C型曲线”的方程序号是 .
15.已知![]() 是定义在[-1,1]上的奇函数, 且当
是定义在[-1,1]上的奇函数, 且当![]() [-1,1]时,
[-1,1]时,![]() ,又
,又
![]() ,则
,则![]() 的最大值是
;若对任意
的最大值是
;若对任意![]() [-1,1]及
[-1,1]及![]() [-1,1]
[-1,1]
都有![]() 成立,则t的取值范围是
.
成立,则t的取值范围是
.
三、解答题:本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤.
16.(12分)
设函数![]() ,其中
,其中![]() 为常数.
为常数.
(1)求证:对任意![]() 都有
都有![]() ;
;
(2)若![]() 求
求![]() 的值.
的值.
17.(12分)
|
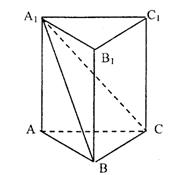
 如图,在直三棱柱ABC—A1B1C1中,截面A1BC⊥侧面A1ABB1,AB=BC=a,直线AC和截面A1BC所成的角为60°.
如图,在直三棱柱ABC—A1B1C1中,截面A1BC⊥侧面A1ABB1,AB=BC=a,直线AC和截面A1BC所成的角为60°.
(1)证明:BC⊥侧面A1ABB1;
(2)求顶点C1到截面A1BC的距离.
18.(14分)
 设
设![]() 为常数,函数
为常数,函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的极大值和极小值;
的极大值和极小值;
(2)若![]() 为增函数,求a的取值范围.
为增函数,求a的取值范围.

19.(14分)

|
(1)求随机变量ξ的分布列;
(2)求Eξ和Dξ的值.
20.(14分)
设动点P的坐标为(![]() ,向量a=(x,0),b=(1,y).
,向量a=(x,0),b=(1,y).
已知(![]() a+ b)⊥(
a+ b)⊥(![]() a- b).
a- b).
(1)求点P的轨迹方程;
(2)设直线l: y=kx-1与点P的轨迹相交于A、B两点,点P的轨迹与x轴正半轴相交
于点M,试推断是否存在实数k,使得以线段AB为直径的圆恰好经过点M?若存
在,求k的值;若不存在,说明理由.
21.(14分)
设等差数列![]() 的各项均为正数,其前n项为Sn,已知
的各项均为正数,其前n项为Sn,已知![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,试推测
,试推测![]() 与
与![]() )的大小关系,
)的大小关系,
并证明你的结论.
数学(理)参考答案
一、选择题
1.C 2.B 3.D 4.A 5.D 6.C 7.A 8.B 9.C 10.B
二、填空题:
11.(-1,1)∪(2,+∞); 12.![]() ;13.60;14.②③;15.1;{
;13.60;14.②③;15.1;{![]() .}
.}
三、解答题:
16.(1)将函数式化简,得![]() ……………………3分
……………………3分
![]()
![]() ……………………………………6分
……………………………………6分
(2)若![]()
![]() (舍去).……9分
(舍去).……9分
![]()
![]() …………………………12分
…………………………12分
17.(1)在侧面A1ABB1内作AD⊥A1B,垂足为D,∵截面A1BC⊥侧面A1ABB1.
∴AD⊥截面A1BC,![]() AD⊥BC.………………………………………………3分
AD⊥BC.………………………………………………3分
∵A1A⊥底面ABC,∴A1A⊥BC. 而AD和A1A是侧面A1ABB1内两相交直线,
∴BC⊥侧面A1ABB1.………………………………………………………………6分
(2)方法一:连CD,则CD是AC在截面A1BC内的射影,
由已知∠ACD=60°.………………………………………………………………10分
由(1)知AB⊥BC,又AB=BC=a,∴AC=![]() a.
a.
在Rt△ADC中,AD=ACsin60°=![]() a.
a.
∵B1C1∥BC,∴∵B1C1∥截面A1BC,∴点B1,C1与截面A1BC等距离,作B1E⊥A1B垂足为E,则B1E⊥截面A1BC,∵A1ABB1为矩形,∴B1E=AD=![]() a.
a.
故顶点C1到截面A1BC的距离是![]() a.……………………………………14分
a.……………………………………14分
方法二:作C1H⊥截面A1BC,垂足为H,连A1H.
∵A1C1∥AC,∴直线A1C1和截面A1BC所成的角为60°.
∵∠C1A1H=60°.…………………………………………………………9分
由(1)知,AB⊥BC,又AB=BC=a,∴AC=![]() ,从而A1C1=
,从而A1C1=![]() .
.
在Rt△A1HC1中,C1H=A1C1sin60°=![]() a.
a.
故顶点C1到截面A1BC的距离是![]() a.……………………………………12分
a.……………………………………12分
方法三:(向量法)
 18.(1)当
18.(1)当![]() 时,
时,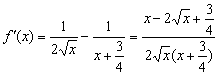 ………………………2分
………………………2分
令![]() ,则
,则![]()
解得![]() …………………………………………………………………4分
…………………………………………………………………4分
又![]() 的定义域是[0,+∞],且当
的定义域是[0,+∞],且当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
![]() 极大值
极大值![]() ,
,![]() 极小值
极小值![]() ………………7分
………………7分
(2)若![]() 为增函数,则
为增函数,则![]() 恒成立.
恒成立.
即![]() 恒成立.
恒成立.![]() ……………………………………10分
……………………………………10分
![]() 恒成立.
恒成立.
![]() 故a的取值范围是[1,
故a的取值范围是[1,![]() …………………………14分
…………………………14分
19.(1)依题意,ξ的可能取值为7,8,9,10.且
P(ξ=7)=![]() ,P(ξ=8)=
,P(ξ=8)=![]() ,
,
|
∴ξ的分布列为
(2)Eξ=7×![]() +8×
+8×![]() +9×
+9×![]() +10×
+10×![]() =8.4.……………………………………11分
=8.4.……………………………………11分
Dξ=(7-8.4)2×![]() +(8-8.4)2×
+(8-8.4)2×![]() +(9-8.4)2×
+(9-8.4)2×![]() +(10-8.4)2×
+(10-8.4)2×![]() =0.84
=0.84
…………………………………………………………………………………………14分
20.(1)由已知(![]() a+ b)·(
a+ b)·(![]() a- b)=0,即3a2-b2=0.
a- b)=0,即3a2-b2=0.
![]()
故点P的轨迹方程是![]() ………………………………6分
………………………………6分
(2)![]()
设点A(![]() ,B(
,B(![]() .则
.则![]() .
.
且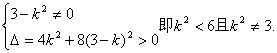 …………………………7分
…………………………7分
又M(![]()
若以AB为直径的圆过点M,则![]()
![]() …………………………10分
…………………………10分
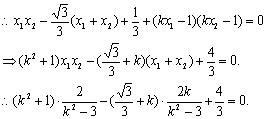
化简整理,得![]() 即
即![]()
![]() ,
,
故存在实数![]() 满足条件.…………………………………………14分
满足条件.…………………………………………14分
21.(1)设数列![]() 的公差为d(d>0),
的公差为d(d>0),
由已知![]()
即![]()
![]()
![]() ………………………………………………5分
………………………………………………5分
(2)![]() ,
,
![]()
![]()
……
由此猜想:当![]() 时,
时,![]() ………………………………………………8分
………………………………………………8分
证明:①当n=2时,![]() 结论成立.
结论成立.
②假设当n=k(k≥2)时结论成立,即![]()
则![]()
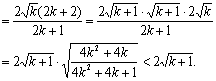
![]() 时结论成立.
时结论成立.
综合①②知,当![]() 时,
时,![]() ;当n=1时,
;当n=1时,![]() ………………14分
………………14分