2006年杭州市第一次高考科目教学质量检测
数学试题卷(理科)
考生须知:
1. 本卷满分150分, 考试时间120分钟.
2. 答题前, 在答题卷密封区内填写学校、班级和姓名.
3. 所有答案必须写在答题卷上, 写在试题卷上无效.
4. 考试结束, 只需上交答题卷.
参考公式
如果事件![]() 互斥,那么
互斥,那么![]() ;
;
如果事件![]() 相互独立,那么
相互独立,那么 ![]() ;
;
如果事件![]() 在一次试验中发生的概率是
在一次试验中发生的概率是![]() ,那么
,那么![]() 次独立重复试验中恰好发生
次独立重复试验中恰好发生![]() 次的概率
次的概率![]() .
.
一. 选择题 : 本大题共10小题, 每小题5分, 共50分. 在每小题给出的四个选项中, 只有一项是符合题目要求的 .
1. (![]() ) 2 等于 ( )
) 2 等于 ( )
(A) – 1 (B) 1 (C) i (D) – 4
2.下列四个极限运算中,正确的是( )
(A)![]() (B).
(B).![]()
(C)![]() (D)
(D) ![]()
3. 函数y=sin(2x+![]() )的图象可由函数y=sin2x的图象经过平移而得到,这一平移过程可以是
( )
)的图象可由函数y=sin2x的图象经过平移而得到,这一平移过程可以是
( )
(A)向左平移![]() (B)向右平移
(B)向右平移![]() (C)向左平移
(C)向左平移![]() (D)向右平移
(D)向右平移![]()
4. ![]() 的展开式中的常数项是 (
)
的展开式中的常数项是 (
)
(A) 20 (B) 80 (C) 160 (D) 960
5. 在数列{an}中,已知a1 = 1, 且当n ≥2时,a1a2 … an = n2,则a3 + a5等于( )
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
6. 下面给出四个命题:
(1) 对于实数m和向量a、b恒有:m(a – b) = ma – mb;
(2) 对于实数m,n和向量a,恒有:(m – n)a = ma – na;
(3) 若ma = mb (m∈R,m ¹ 0), 则a = b;
(4) 若ma = na (m,n∈R,a ≠ 0), 则m = n.
其中正确命题的个数是 ( )
(A)1 (B)2 (C)3 (D)4
7. ![]() = ( )
= ( )
![]()
8. 已知f (x) = 1 – ( x – a )(x – b ),并且m,n是方程f (x) = 0的两根,则实数a, b, m, n的大小关系可能是( )
(A) m < a < b < n (B) a < m < n < b
(C) a < m < b < n (D) m < a < n < b
9.已知f ( x ) = ![]() , 则f ( – 9 ) 等于( )
, 则f ( – 9 ) 等于( )
(A)–1. (B)0. (C)1. (D)3.
10. 从集合{1,2,3,……10}中,选出由5个数组成的子集,使得这5个数中的任何两个数的和不等于11,则这样的子集共有 ( )
(A)10个 (B)16个 (C)20个 (D).32个
二.填空题: 本大题有4小题, 每小题4分, 共16分. 把答案填在答题卷的相应位置.
11. 函数y=![]() 的单调递增区间是
.
的单调递增区间是
.
12 若血色素化验的准确率是p, 则在10次化验中,最多一次不准的概率为 .
13. 已知a = (1,–2),b = ( 4, 2), a与( a –b )的夹角为q, 则 cosq等于 .
14. 已知命题p: x – 2 < a (a > 0 ), 命题q: x 2 – 4 < 1 , 若p是q的充分不必要条件,则实数a的取值范围是 .
三. 解答题: 本大题有6小题, 每小题14分,共84分. 解答应写出文字说明, 证明过程或演算步骤.
15. (本小题满分14分)
已知a、b、c是△ABC中A、B、C的对边, 关于x的方程b (x 2 + 1 ) + c (x 2–1 ) –2ax = 0 有两个相等的实根, 且sinCcosA – cosCsinA=0, 试判定△ABC的形状.
16. (本小题满分14分)
解关于 x的不等式lg(2ax) – lg(a+ x ) < 1
17.(本小题满分14分)
已知向量a = ( sinx , 0 ), b = (cosx, 1), 其中 0 < x <![]() , 求
, 求![]() a -
a -![]() b 的取值范围.
b 的取值范围.
18 . (本小题满分14分)
某造船公司年最高造船量是20艘. 已知造船x艘的产值函数R (x)=3700x + 45x2 – 10x3(单位:万元), 成本函数为C (x) = 460x + 5000 (单位:万元). 又在经济学中,函数f(x)的边际函数Mf (x)定义为: Mf (x) = f (x+1) – f (x). 求:(提示:利润 = 产值 – 成本)
(1) 利润函数P(x) 及边际利润函数MP(x);
(2) 年造船量安排多少艘时, 可使公司造船的年利润最大?
(3) 边际利润函数MP(x)的单调递减区间, 并说明单调递减在本题中的实际意义是什么?
19. (本小题满分14分)
10个实习小组在显微镜下实测一块矩形蕊片,测得其长为29 μm,30 μm,31 μm的小组分别有3个,5个,2个,测得其宽为19 μm,20 μm, 21 μm的小组分别有3个,4个,3个,设测量中矩形蕊片的长与宽分别为随机变量ξ和η, 周长为μ .
(1) 分别在下表中,填写随机变量ξ和η的分布律;
(2) 求周长μ的分布律, 并列表表示;
(3) 求周长μ的期望值.
20. (本小题满分14分)
设函数f
( x ) = ![]() (a ÎN*), 又存在非零自然数m, 使得f (m ) = m , f (– m ) < –
(a ÎN*), 又存在非零自然数m, 使得f (m ) = m , f (– m ) < –![]() 成立.
成立.
(1) 求函数f ( x )的表达式;
(2) 设{an}是各项非零的数列, 若![]() 对任意nÎN*成立, 求数列{an}的一个通项公式;
对任意nÎN*成立, 求数列{an}的一个通项公式;
(4) 在(2)的条件下, 数列{an}是否惟一确定? 请给出判断, 并予以证明.
2006年杭州市第一次高考科目教学质量检测
数学参考评分标准(理科)
一. 选择题 (本大题共10小题, 每小题5分, 共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | B | A | C | B | D | C | A | C | D |
二.填空题: (本大题有4小题, 每小题4分, 共16分)
11. (–¥ ,3] .
12 ![]() .
.
13. ![]() .
14. 0
< a £
.
14. 0
< a £![]() – 2 (或q < x £ p , 其中q > 0, p£
– 2 (或q < x £ p , 其中q > 0, p£![]() – 2)
.
– 2)
.
三. 解答题: (本大题有6小题, 每小题14分,共84分)
15. (本小题满分14分)
由(b + c)x 2 –2ax + (b – c ) = 0有相等实根,
得 ⊿= 4a 2 – 4( b + c )(b – c) = 0, 3分
即 a 2 + c 2 – b 2 = 0 ,
∴ B = 90° . 3分
又sinCcosA – cosCsinA=0 ,
得 sin (C – A) = 0 . 2分
∵–![]() < C – A <
< C – A < ![]() ,
2分
,
2分
∴ A = C,
∴△ABC是B为直角的等腰直角三角形. 2分
16. (本小题满分14分)
由![]() ,得a > 0 , x > 0 .
3 分
,得a > 0 , x > 0 .
3 分
不等式化成: lg(2ax) < lg(10a + 10x) 3分
得2ax < 10a + 10x
(a – 5)x < 5a 2分
当 0 < a < 5时, a – 5 < 0, 解得x >0, 2分
当 a = 5时,不等式为0•x < 25, 得x > 0, 2分
当 a > 5时, a – 5 > 0, 解得0 < x <![]() . 2分
. 2分
17.(本小题满分14分)
解1: ![]() a -
a - ![]() b 2 =
(
b 2 =
(![]() sinx–
sinx–![]() cosx, -
cosx, -![]() ) 2
2分
) 2
2分
= (![]() sinx–
sinx–![]() cosx)2 +
cosx)2 +![]() 3 分
3 分
= sin2(x – ![]() ) +
) +![]() .
3分
.
3分
Π0 < x
< ![]() , ∴–
, ∴–![]() < x -
< x -![]() <
< ![]() ,
2分
,
2分
∴ 0 £ sin2(C–
![]() ) <
) < ![]() ,
2分
,
2分
得 ![]() a -
a -![]() b Î [
b Î [![]() ,
, ![]() ).
2分
).
2分
解2: ![]() a –
a – ![]() b 2 =
b 2 = ![]() a 2 –
a 2 – ![]() a·b +
a·b + ![]() b 2
2分
b 2
2分
= ![]() sin2 –
sin2 –
![]() sinxcosx +
sinxcosx + ![]() (cos2x +1)
2分
(cos2x +1)
2分
=![]() sin2–
sin2–![]() sinxcosx +
sinxcosx + ![]() cos2x +
cos2x + ![]()
= (![]() cosx –
cosx – ![]() sinx)2 +
sinx)2 +![]() 2 分
2 分
= sin2(x – ![]() ) +
) +![]() .
2分
.
2分
Π0 < x
< ![]() , ∴–
, ∴–![]() < x -
< x -![]() <
< ![]() ,
2分
,
2分
∴ 0 £ sin2(C–
![]() ) <
) < ![]() ,
2分
,
2分
得![]() a -
a - ![]() b 2 Î [
b 2 Î [![]() ,
, ![]() ).
2分
).
2分
18 . (本小题满分14分)
解:
(1) P(x) = R (x) – C (x) = – 10x3 + 45x2 + 3240x – 5000 (xÎN且xÎ[1, 20]); 2分
MP (x) = P ( x + 1 ) – P (x) = – 30x2 + 60x +3275 (xÎN且xÎ[1, 20]). 2分
(2) P`(x) = – 30x2 + 90x + 3240 = – 30( x +9 )(x – 12) (xÎN且xÎ[1, 20]) 3分
当1< x < 12时, P`(x) > 0, P(x)单调递增,
当 12 <x < 20时, P`(x) < 0 , P ( x ) 单调递减.
∴ x = 12 时, P(x)取最大值, 3分
即, 年建造12艘船时, 公司造船的年利润最大. 1分
(3) 由MP(x ) = – 30( x – 1) 2 + 3305 (xÎN且xÎ[1, 20]).
∴当1< x £ 20时,MP (x)单调递减. 2分
MP (x)是减函数说明: 随着产量的增加,每艘利润与前一台比较,利润在减少.1分
19. (本小题满分14分)
(1)
| 长度ξμm | 29 | 30 | 31 |
| P | 0.3 | 0.5 | 0.2 |
| 宽度ημm | 19 | 20 | 21 |
| P | 0.3 | 0.4 | 0.3 |
4分
(2)P(ζ = 96) = 0.3´0.3 = 0.09;
P(ζ = 98) = 0.3´0.4 + 0.5´0.3 = 0.27;
P(ζ = 100) = 0.5´0.4 + 0.2´0.3 + 0.3´0.3 = 0.35;
P(ζ = 102) = 0.2´0.4 + 0.5´0.3 = 0.23;
P(ζ = 104) = 0.2´0.3 = 0.06.
得,周长分布律如下表所示
| 周长μ μm | 96 | 98 | 100 | 102 | 104 |
| P | 0.09 | 0.27 | 0.35 | 0.23 | 0.06 |
6分
(3)方法1(利用周长的分布计算)
Eμ= 96×0.09+98×0.27+100×0.35+102×0.23+104×0.06=99.8 4分
方法2(利用矩形长与宽的期望计算)
由长和宽的分布率可以算得
Eξ=29×P(ξ=29)+30×P(ξ=30)+31×P(ξ=31)
=29×0.3+30×0.5+31×0.2=29.9
Eη=19×P(η=19)+20×P(η=20)+21×P(η=21)
=19×0.3+20×0.4+21×0.3=20
由期望的性质可得
Eμ=2(Eξ+Eη)=2×(29.9+20)=99.8 4分
20. (本小题满分14分)
(1) 由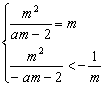 , 得
, 得![]() 2分
2分
由(1)得 m
= ![]() ,
,
当a = 2时, m = 2, 满足(2)式;
当a = 3时, m
= 1, 不满足(2)式, 舍去. 得f ( x ) = ![]() ( x ¹ 1).
3分
( x ¹ 1).
3分
(2) 由条件得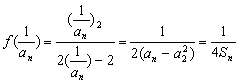
∴ an(1 – an) = 2Sn (3) , 2分
令n = 1,得 a1 = –1,
又an – 1 (1 – an – 1 ) = 2S n – 1 , ∴( an + a n – 1 )( an + 1 – a n – 1 )= 0,
由an – a n – 1 = – 1 , a1 = –1,得{an}是首项为– 1, 公差为– 1的等差数列,
∴ an= – 1 + (n – 1 )( – 1)= – n . 3分
(3) 由(2)知,满足条件的数列不惟一.
考虑到a1 ¹ 1, 由 an = – a n – 1 及an – a n – 1 = – 1和a1 = –1,
构造数列{ –1, –2, 2,–2, –3, – 4, … , – n +2, … }. 2分
用数学归纳法证明,该数列满足(3)式,
当n = 1, 2, 3, 4, 5时,直接代入可得(3)式成立,
假设n = k ( k ³ 5)时,(3)成立, 则n = k + 1时,
Sk+1 =S k + a k+1
= ![]() ak(1 – ak) + a k + 1 =
ak(1 – ak) + a k + 1 = ![]() (–a k +1)(1 + ak+1) + a k + 1 =
(–a k +1)(1 + ak+1) + a k + 1 =![]() ak+1(1 – a k+1).
ak+1(1 – a k+1).
所以n = k + 1时(3)式成立, 即该数列满足题设条件.
得满足条件的数列不惟一.
构造数列也可能是:
{ –1, 1, –1, –2, –3, – 4, … , – n , … };
{ –1, –2,2, –2, 2, –2, … , (–1) n – 1 2 , … }( n > 1 )
{ –1, –2,2, –2, –3, – 4, … , – n , … }等等.