中山市2005—2006学年度第一学期期末统一检测
高三数学试卷
本试卷分第I卷（选择题）、第II卷（非选择题）两部分。共150分，考试时间120分钟。
第Ⅰ卷（选择题共50分）
注意事项：
1、答第I卷前，考生务必将自己的姓名、统考考号、座位号、考试科目用铅笔涂写在答题卡上。
2、每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题上。
3、考试结束，将答题卡交回，试卷不用上交。
一、选择题：（每题5分，共50分）
1、已知集合A={0，2，3}，B={
、
}，且
，则B的子集的个数是
A、4 B、8 C、16 D、15
2、平面向量
与向量
夹角为
，且
，则=
A、（2，1）或
B、
或
C、（2，1） D、
3、下列各式中，值为
的是
A、sin15°cos15°
B、
C、
D、
4、不等式
的解集为
A、
B、
C、
D、
5、设
、
是异面直线，那么
A、必然存在唯一的一个平面同时平行、
B、必然存在唯一的一个平面同时垂直、
C、过存在唯一的一个平面平行于
D、过存在唯一的一个平面垂直于
6、若
，则
的一个值为（ ）
A、1-2
B、1+2
C、2-
D、2+
7、如图，点P在正方形ABCD所在的平面外，PD⊥平面ABCD，PD=AD，则PA与BD所成角的度数为
A、30° B、45° C、60° D、90°
8、已知等差数列
满足
=0，则有
A、
B、
C、
D、
9、设、
，且
，则有（ ）
A、
B、
C、
D、
10、已知定义域为R的函数
满足
，当
时，单调递增，如果
且
，则
的值
A、恒小于0 B、恒大于0 C、可能为0 D、可正可负
|
高三数学试卷
第II卷（非选择题 满分100分）
| 题号 | 二 | 15 | 16 | 17 | 18 | 19 | 20 | 总分 | 总分人 | 复分人 |
二、填空题（每题5分，共20分）
11、若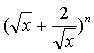
的展开式中的第5项为常数项，则
；
12、
的值为 ；
13、在ΔABC中，角A、B、C所对的边分别为、、
，已知A=60°，
，三角形ABC的面积为
，则的值为 ；
14、规定记号“
”表示一种运算，即
，若
，则
的值为 ；函数
的值域为
；
三、解答题（本大题共6小题，共80分）
15．（本小题13分）
若
=
，
，
，
,
设
;
(1)求 的最小正周期；(7分) (2)若
，
，求 的值域。(6分)
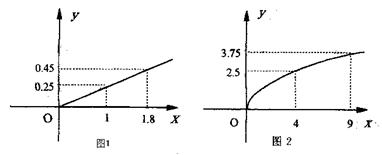
16．（本小题13分）某民营企业生产A、B两种产品，根据市场调查与预测，A产品的利润与投资成正比，其关系如图1，B产品的利润与投资的算术平方根成正比，其关系如图2（注：利润与投资单位：万元）
（1）分别将A、B两种产品的利润表示为投资的函数关系式，并写出它们的函数关系式(6分)
（2）该企业已筹集到10万元资金，并全部投入A、B两种产品的生产，问：怎样分配这10万元投资，才能使企业获得最大利润，其最大利润约为多少万元（精确到1万元）(7分)
|
17．（本小题13分）有三张大小形状质量完全相同的卡片，三张卡片上分别写有0，1，2三个数字，现从中任抽一张，其上面的数字记为x，然后放回，再抽一张，其上面的数字记为y，记
=xy，求：
（1）的分布列；(8分)（2）的期望. (5分)
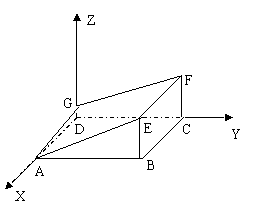
18．（本小题满分13分）如图所示的多面体是由底面为
的长方体被截面
所截而得，其中
,
,
,
,若如图所示建立空间直角坐标系：
①求
和点
的坐标；(3分)
②求异面直线
与
所成的角；(5分)
③求点C到截面的距离；(5分)
19．（本小题14分）已知数列
的前n项和为
，且满足
，
．
（1）问：数列
是否为等差数列？并证明你的结论；(5分)
（2）求和
；(5分)
（3）求证：
(4分)
20．（本小题满分14分）已知函数f(x)＝lnx，g(x)＝ax2＋bx，a≠0.
（Ⅰ）若b＝2，且h(x)＝f (x)－g (x)存在单调递减区间，求a的取值范围；(7分)
（Ⅱ）设函数f (x)的图象C1与函数g (x)图象C2交于点P、Q，过线段PQ的中点作x轴的垂线分别交C1，C2于点M、N，证明C1在点M处的切线与C2在点N处的切线不平行. (7分)