海门市2005—2006学年高三年级第二次教学质量抽测
数 学
注意事项:
1、 本试卷分第Ⅰ卷和第Ⅱ卷两部分,满分150分。
2、 答卷前,考生务必将自己的姓名、考试证号、考试科目等填写在答题卡和答题纸规定的地方,并用2B铅笔在答题卡上相应的位置涂黑。
3、 选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后再涂其它答案。
4、 交卷时,只交答题卡和答题纸。
第Ⅰ卷 选择题(满分60分)
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1、函数![]() 的最小正周期是( )
的最小正周期是( )
![]()
![]()
![]()
![]()
2、若![]() ,则下列结论不正确的是( )
,则下列结论不正确的是( )
![]()
![]()
![]()
![]()
3、函数![]() 的反函数为( )
的反函数为( )
![]()
![]()
![]()
![]()
4、已知等差数列的前n项和为Sn,若a4=18-a5,则S8等于( )
A.18 B.36 C.54 D.72
5、在三角形ABC中,”A<600”是”sinA<![]() ”的( )
”的( )
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分也不必要条件
6、已知直线m, n与平面![]() ,给出下列四个命题:
,给出下列四个命题:
①若![]() ,则m//n
,则m//n
②若![]() ,则
,则![]()
③若![]() ,则
,则![]()
④若![]() ,m, n共面,则m//n
,m, n共面,则m//n
其中真命题的个数是( )
 A、0个 B、1个 C、2个 D、3个
A、0个 B、1个 C、2个 D、3个
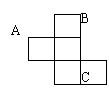
7、如图是一个无盖正方体盒子的表面展开图,
A,B,C为其上的三个顶点,则在原正方体中,
等于( )
A.450 B.600 C.900 D.1200
8、已知点P在曲线![]() 上移动,点P处切线的倾斜角为
上移动,点P处切线的倾斜角为![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
![]()
![]()
![]()
![]()
9、若![]() ,则a的取值范围是( )
,则a的取值范围是( )
![]()
![]()
![]()
![]()
10、函数![]() 的图象可由
的图象可由![]() 的图象按向量
的图象按向量![]() ( )平移而得
( )平移而得
![]()
![]()
![]()
![]()
11、定义在R上的函数f(x)既是奇函数又是偶函数,若f(x)的最小正周期是![]() ,且当
,且当![]() 时,f(x)=sinx,则
时,f(x)=sinx,则![]() 的值为( )
的值为( )
![]()
![]()
![]()
![]()
12、已知O,A,B,C是不共线的四点,若存在一组正实数![]() ,使得
,使得![]() ,则三个角
,则三个角![]() ( )
( )
A、都是钝角 B、至少有两个钝角 C、恰有两个钝角 D、至多有两个钝角
第Ⅱ卷 选择题(满分90分)
二、填空题:本大题共6小题,每小题4分,共24分。把答案填写在答题卡相应位置上。
13、已知![]() ,则
,则![]() =
。
=
。
14、已知函数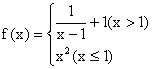 ,则
,则![]() 的解集为
。
的解集为
。
15、按国际乒乓球比赛的新规则,乒乓球的直径由38mm改为40mm,则乒乓球的面积增加了
![]() (mm)2.
(mm)2.
16、通过测量知道,某电子元件每降低60C,电子数目就减少一半,已知在零下340C时,该电子元件的电子数目为3个。则在室温260C时,该元件的电子数目为 个。
17、已知集合![]() ,若
,若![]() ,则a的取值范围为
。
,则a的取值范围为
。
18、对于任意实数x ,y ,定义运算![]() ,其中a, b, c为常数,等号右边的运算是通常意义的加、乘运算。现已知1*2=3,2*3=4,且有一个非零的实数m,使得对任意实数x,都有x*m=x,则m= 。
,其中a, b, c为常数,等号右边的运算是通常意义的加、乘运算。现已知1*2=3,2*3=4,且有一个非零的实数m,使得对任意实数x,都有x*m=x,则m= 。
三、解答题:本大题共5小题,共66分。解答应写出文字说明、证明过程或演算步骤。
19、(本小题满分12分)
已知点A(3,0),B(0,3),C![]()
(1)
若![]() ,求
,求![]() 的值;
的值;
(2)
若![]() ,且
,且![]() ,求
,求![]() 与
与![]() 的夹角。
的夹角。
20、(本小题满分13分)
已知等差数列![]() 的首项
的首项![]() ,公差
,公差![]() ,且其第二、第五、第十四项分别是等比数列
,且其第二、第五、第十四项分别是等比数列![]() 的第二、第三、第四项。
的第二、第三、第四项。
(1)
分别求数列![]() 与
与![]() 的通项公式;
的通项公式;
(2)
设数列![]() 对任意
对任意![]() 均有
均有![]() 成立,求
成立,求![]() 的值。
的值。
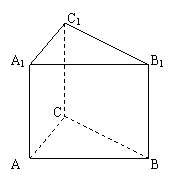 21、(本小题满分14分)
21、(本小题满分14分)
已知直三棱柱ABC—A1B1C1中,![]() AC=CB=AA1=2,
AC=CB=AA1=2,
D是AB的中点。
(1)
求证:CD![]() 平面ABB1A1
平面ABB1A1
(2) 求二面角D—A1C—A的大小;
(3) 求点C1到平面A1CD的距离。
22、(本小题满分14分)
函数f(x)是定义在[-1,1]上的偶函数,当![]() 时,f(x)=x3-3ax(a为常数)。
时,f(x)=x3-3ax(a为常数)。
(1)
当![]() 时,求f(x)的解析式;
时,求f(x)的解析式;
(2) 求f(x)在[0,1]上的最大值。
23、(本小题满分13分)
设f(x)是区间(0,1)上的函数,且f(x)>0.
(1)
如果f(x)+f(1-x)![]() 1对任意的
1对任意的![]() 恒成立,证明:当
恒成立,证明:当![]() 且
且![]() 时,
时,![]() ;
;
(2)
如果![]() 对任意的
对任意的![]() 恒成立,证明f(x)为常数函数。
恒成立,证明f(x)为常数函数。
参考答案
一、选择题:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| B | D | C | D | A | D | B | B | D | D | C | B |
二、填空题:
13、![]() 14、
14、![]() 15、156
15、156
16、3072 17、![]() 18、4
18、4
三、解答题:
19、解:(1)![]()
![]()
![]()
(2)![]()
![]()
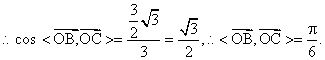
20、解:(1)![]()
![]()
而,![]()
(2)![]()
![]()
![]()
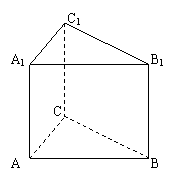 21、解:(1)因为AC=CB,所以,CD
21、解:(1)因为AC=CB,所以,CD![]() AB,
AB,
又因为ABC—A1B1C1是直三棱柱,所以CD![]() AA1,
AA1,
|
![]()
![]() (2)取AC中点E,则DE
(2)取AC中点E,则DE![]() AC,得:DE
AC,得:DE![]() 平面ACC1A1,
平面ACC1A1,
|
![]()
|
在![]() 中,DE=0.5AC=1。
中,DE=0.5AC=1。
EH=![]()
![]()
(3)
由![]()
22、解:(1)设![]() ,则
,则![]() ,所以
,所以![]() ,又因为
,又因为![]() 是偶函数,所以
是偶函数,所以 ![]()
(2)当![]() 时:
时:![]()
ⅰ)当![]() 时,
时,![]() 恒成立,
恒成立,![]() 单调减。
单调减。![]()
ⅱ)当![]() 时,由
时,由![]()
①当![]() 时,
时,![]() 恒成立,
恒成立,![]() 单调增。
单调增。![]()
②当![]() 时,由下表知:
时,由下表知:
| x |
|
|
|
|
| + | 0 | - |
| f(x) | 增 | 减 |
![]()
综上所述:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]()
23、解:(1)设![]()
所以:![]()
(2)由![]() 得:
得:![]()
![]()
而: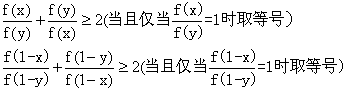
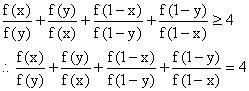
故:![]() 对任意的
对任意的![]() 都成立。
都成立。
因而:f(x)为常数函数。