河南省实验中学2005—2006学年度高三年级月考试题

 数学试卷（理科）

YCY

本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.共150分，考试时间120分钟.

第I卷（选择题，共60分）

注意事项：

1．答第I卷前，考生务必将自己的姓名、准考证号、试题科目用铅笔涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上。

3．考试结束，监考人将本试卷和答题卡一并收回。

参考公式：如果事件A、B互斥，那么P（A+B）=P（A）+P（B）

　　　　  如果事件A、B相互独立，那么P（A·B）=P（A）·P（B）

　　　　  如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k

次的概率P_n（k）=

一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，有且只有一项符合题目要求。

1．设全集U=R，集合M={xx<－1},N={xx>1}，则下列关系中正确的是　　　　　　　 （　　）

　　　 A．M=N　　　　　　　　　B．N　 M 　　　　　　　C．M　 N　　　　　　　 D．N∩CuM=φ

2．等差数列{a_n}的前n项和为S_n，若S₆－S₂=4，则S₈的值是　　　　　　　　　　　　　　　　（　　）

　　　 A．2　　　　　　　　　　　　B．4　　　　　　　　　　　　C．6　　　　　　　　　　　　D．8

3．函数y=2^x+1(－1≤x<0)的反函数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．y=1+log₂x(x>0)　　　　　　　　　　　　　　　　　 B．y=－1+log₂x(x>0)

　　　 C．y=1+log₂x(1≤x<2)　　　　　　　　　　　　　　 D．y=－1+log₂x(1≤x<2)

4．若圆x²+y²+mx－=0与直线y=－1相切，则m值为　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　B．±　　　　　　　　 C．2　　　　　　　　　　　　D．－2

5．已知函数，且以2为最小正周期，并当x=2时取

　 得最大值，则的一个值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　 B．　　　　　　　　 C．　　　　　　　　　　D．

6．l是三棱柱底面所在平面内的直线，在三棱柱的三条侧棱和另一个底面的三条边所在的6

　条直线中，与l构成异面直线的条数不可能是　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．3　　　　　　　　　　　　B．4　　　　　　　　　　　　C．5　　　　　　　　　　　　D．6

7．已知向量a=2, b=2， a与b的夹角为60°，则a－b与b的夹角是　　　　　　　　　（　　）

　　　 A．30°　　　　　　　　　 B．60°　　　　　　　　　 C．90°　　　　　　　　　 D．120°

8．已知为常数），则b的值是　　　　　　　　　　　　　　　 （　　）

　　　 A．4　　　　　　　　　　　　B．0　　　　　　　　　　　　C．2　　　　　　　　　　　　D．－4

9．若双曲线的一个焦点与抛物线y²=4x的焦点重合，则双曲线两条渐近线的

　 夹角为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．30°　　　　　　　　　 B．60°　　　　　　　　　 C．120°　　　　　　　　 D．150°

10．若直线相切，则a的值是　　　　　　　　　　　　　　（　　）

　　　 A．1　　　　　　　　　　　　B．±1　　　　　　　　　　 C．　　　　　　　　　　　D．－

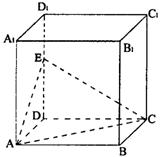
11．已知正四棱柱ABCD—A₁B₁C₁D₁中，E在侧

　　棱DD₁上，且截面EAC与底面ABCD成

45°角，则二面角A—EC—D为（　　）

　　　 A．30°　　　　　　　　　 B．45°　　　　　　　　　

　　　 C．60°　　　　　　　　　 D．90°

12．平面向量也叫二维向量，二维向量的坐标

表示及其运算可以推广到n(n≥3)维向量，

n维向量可用（x₁，x₂，x₃，x₄，…,x_n）表示.

设a=(a₁, a₂, a₃, a₄，…, a_n)，b=（b₁, b₂, b₃, b₄,…,b_n），规定向量a与b夹角θ的余弦为

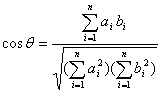
　　 当a=(1, 1,1,1…,1)，b=(－1, －1, 1, 1,…,1)时，cosθ=　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　B．　　　　　　　　 C．　　　　　　　　D．

第Ⅱ卷（非选择题，共90分）

注意事项：

1．第II卷共6页，用钢笔或圆珠笔直接答在试题卷上，不要在答题卡上填涂。

2．答卷前将密封线内的项目填空清楚。

二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上。

13．已知复数z满足z(1+i)=2，则z的虚部是　　　　　   

14．不等式的解集为　　　　　  

15．的展开式中常数项为　　　　　   .（用数字作答）

16．一个袋子里装有大小相同的3个红球与2个白球，从中同时取出2个球，则其中取出红球个数的数学期望为　　　　   .（用数字作答）

三、解答题：本大题共6小题，共74分。解答应写出文字说明、证明过程或演算步骤。

17．（本小题满分12分）

设甲、乙两名同学投篮，甲投中的概率为0.7，乙投中的概率为0.8，两人是否投中相互之间没有影响.求：

（I）两人各投篮1次，只有1人投中的概率；

（II）每人各投篮2次，甲投中1次、乙投中2次的概率.

18．（本小题满分12分）

如图，四棱锥P—ABCD的底面是AB=2，BC=的矩形，侧面PAB是等边三角形，且侧面PAB⊥底面ABCD.

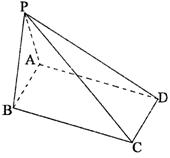
（I）证明：侧面PAB⊥侧面PBC；

（II）求侧棱PC与底面ABCD所成的角；

（III）求直线AB与平面PCD的距离.

19．（本小题满分12分）

　 求函数在[1，3]上的最大值和最小值.

20．（本小题满分12分）

已知锐角

（I）求sin(A+B)的值；

（II）设m=(sinA, sinB), n=(cosB, －cosA), 且m·n=，求tanA的值.

21．（本小题满分12分）

设椭圆的左焦点为F，上顶点为A，过点A与AF垂直的直线分别交椭圆与x轴正半轴于P、Q两点，且.

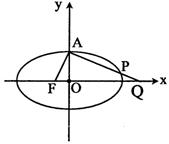
（I）求椭圆离心率e；

（II）若过A、Q、F三点的圆恰好与直线

相切，求椭圆方程.

22．（本小题满分14分）

在数列{a_n}中，.

（I）用数学归纳法证明：a_n>2(n∈N*);

（II）对于n∈N*，证明

　　（i）

　　（ii）a₁+a₂+a₃+…+a_n<2n+1

数学试卷（理科）参考答案

一、选择题：

　　CDDBB　DDABA CA

二、填空题

　 13．－1　　 14．　15．84　　　 16．1.2

三、解答题

17．解：（I）记“甲投篮1次投中”为事件A，“乙投篮1次投中”为事件B，则P（A）=0.7，P（B）=0.8，由题意，A、B是相互独立事件.

　　两人各投篮1次，只有1人投中的概率

　　…………（3分）

　　=0.7×(1－0.8)+(1－0.7)×0.8

　　=0.38……………………………………………………………………………………（5分）

（II）因为甲投篮2次，投中1次概率P₁=0.7×(1－0.7)=0.42……………………（7分）

　　 乙投篮2次，投中2次的概率P₂=0.8²=0.64…………………………………（9分）

　　 所以每人各投篮2次，甲投中1次、乙投中2次的概率

　　 P=P₁×P₂=0.42×0.64=0.2688……………………………………………………… （12分）

18．（I）证明：在矩形ABCD中，BC⊥AB

　　又∵面PAB⊥底面ABCD侧面PAB∩底面ABCD=AB

　　∴BC⊥侧面PAB…………………………（2分）

　　又∵BC侧面PBC

　　∴侧面PAB⊥侧面PBC………………… （4分）

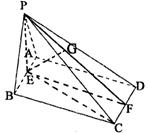
（II）解：取AB中点E，连结PE、CE

　　又∵△PAB是等边三角形

　　∴PE⊥AB

　　又∵侧面PAB⊥底面ABCD，∴PE⊥面ABCD

　　∴∠PCE为侧棱PC与底面ABCD所成角……………………………………………（6分）

　　

　　在Rt△PEC中，∠PCE=45°为所求…………………………………………（8分）

（Ⅲ）解：在矩形ABCD中，AB//CD

　　∵CD侧面PCD，AB侧面PCD，∴AB//侧面PCD

取CD中点F，连EF、PF，则EF⊥AB

又∵PE⊥AB　　∴AB⊥平面PEF

又∵AB//CD　　∴CD⊥平面PEF

∴平面PCD⊥平面PEF…………………………………………………………（10分）

作EG⊥PF，垂足为G，则EC⊥平面PCD

在Rt△PEF中，EG=为所求……………………………… （12分）

19．解：……………………………………………………（2分）

由

化简得x²－x－2=0　解得x₁=－1(舍)或x₂=2………………………………（4分）

当x∈（1，2）时，>0 　f(x)在x∈（1，2）上单调递增，

当x∈（2，3）时，<0 　f(x)在x∈（2，3）上单调递减…………（6分）

又f(x)在[1，3]上连续

所以f(2)=ln2－为函数f(x)的极大值………………………………………（8分）

又∵f(1)=0　　f(3)=ln3－1>0

∴f(3)>f(1) 所以f(1)=0是函数f(x)在[1，3]上的最小值，f(2)=ln2－为f(x)在[1，3]的最大值………………………………………………………………………………（12分）

20．解：（I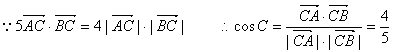）……（2分）

∴sinC=

sin(A+B)=sin(π－C)=sinC=………………………………………………（4分）

（II）m·n=sinAcosB－cosAsinB=　①…………………………………………（6分）

sin(A+B)=sinAcosB+cosAsinB=　②

由①，②得sinAcosB=

　　　　　 cosAsinB=

进而得tanB=tanA　③……………………………………………………（8分）

∵

　 ④

将③代入④，得tan²A－4tanA－2=0

…………………………………………（12分）

21．解：（I）设Q（x₀，0）由F（－c，0）（其中）、A（0，b）

知

………………………………（2分）

设，得

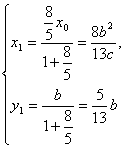因为点P在椭圆上，所以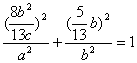…………（5分）

整理得2b²=3ac，即2(a²－c²)=3ac

两边同除以a²记

解得e=，或e=－1（舍去）

故椭圆的离心率e=…………………………………………………………（8分）

（II）由（I），

于是F（－a，0） Q，△AQF的外接圆圆心为（a，0）

半径r=FQ=a

因为这个圆与直线相切，所以

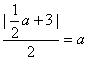，解得a=2

∴c=1，b=，所求椭圆方程为………………………………（12分）

22．（1）证明：（1）当n=1时，a₁=>2，结论成立………………………………（1分）

　 （2）假设n=k(k≥1)不等式a_k>2成立

　　　　当

　　　　

　　　　由a_k>2得a_k+1－2>0即a­_k+1>2

　　　　说明当n=k+1时，不等式也成立

　　　　根据（1）和（2），可知不等a_­n>2对于n∈N*都成立。……………………（5分）

（II）证明：（i）由（I）可知a_n>2(n∈N*)

∴a_n+1－2>0　a_n－2>0

则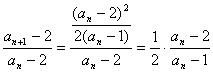…………………………………………（8分）

………………………………（10分）

（ii）由（i）可知，当n≥2时，

…（12分）

则

当，不等式也成立，故对于任意n∈N*，都有

a₁+a₂+a₃+…+a_n<2n+1………………………………………………………………（14分）