攀钢一中2005~2006第一学期中期统一检测试卷
高 三 数 学(理)
命题人:攀钢一中 钟世美
注意事项:
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟。
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合![]() ,
,![]() ,则
,则![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 或
或![]()
2.设![]() :集合
:集合![]() 是集合
是集合![]() 的子集;
的子集;![]() :集合
:集合![]() 是集合
是集合![]() 的子集或
的子集或![]() 的子集。那么
的子集。那么![]() ,
,![]() 的真假是
的真假是
A.![]() 真
真![]() 真 B.
真 B.![]() 真
真![]() 假 C.
假 C.![]() 假
假![]() 真 D.
真 D.![]() 假
假![]() 假
假
3. 已知数列![]() ,那么“对任意的
,那么“对任意的![]() ,点
,点![]() 都在直线
都在直线![]() 上”是“
上”是“![]() 为等差数列”的
为等差数列”的
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分又非必要条件
4.函数![]() 是
是
A.奇函数 B.偶函数 C.非奇非偶函数 D.以上都不对
5. 已知等差数列![]() 的公差为2,若
的公差为2,若![]() 成等比数列,则
成等比数列,则![]() 等于
等于
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
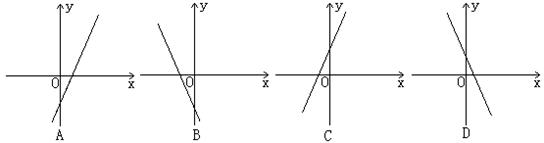
6.若函数![]() 的图象的顶点在第四象限,则函数
的图象的顶点在第四象限,则函数![]() 的图象是
的图象是
7.若![]() 的内角满足
的内角满足![]() ,
,![]() ,则
,则![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
8.若![]() 与
与![]() 在区间
在区间![]() 上都是减函数,则
上都是减函数,则![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.先将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,再将所得图象关于
个单位长度,再将所得图象关于![]() 轴对称,则所得图象对应的函数解析式为
轴对称,则所得图象对应的函数解析式为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
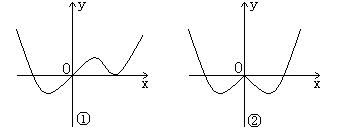
10.已知图①中的图象对应的函数为![]() ,则图②中的图象对应的函数只可能是
,则图②中的图象对应的函数只可能是
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.设数列![]() 满足
满足![]() (
(![]() 且
且![]() ,
,![]() )若
)若![]() ,则
,则![]() 的值为
的值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.![]() 是定义在
是定义在![]() 上的以3为周期的奇函数,且
上的以3为周期的奇函数,且![]() ,则方程
,则方程![]() 在区间(0,6)内解的个数的最小值是
在区间(0,6)内解的个数的最小值是
A.2 B.3 C.4 D.5
攀钢一中2005~2006第一学期中期统一检测试卷
高 三 数 学(理)
总分表
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得分 |
|
|
|
|
|
|
|
|
|
第Ⅰ卷答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
第Ⅱ卷(非选择题 共90分)
| 得分 | 阅卷人 |
|
|
|
二、填空题(本大题4个小题,每小题4分,共16分,只填结果,不要过程)
13.已知函数![]() ,则
,则![]() _______.
_______.
14.若![]() ,则
,则![]() _______.
_______.
15.若函数![]() 在
在![]() 上为减函数,则实数
上为减函数,则实数![]() 、
、![]() 的取值范围是 ______。
的取值范围是 ______。
16.北京市为成功举办2008年奥运会,决定从2003年到2007年5年间更新市内现有全部出租车。若每年更新的车辆数比前一年递增10%,则2003年底更新的车辆数应为现有总车辆数的________(填百分数,精确到0.1。参考数据:![]() ,
,![]() )
)
三、解答题:本大题6个小题,共74分.解答要写出必要的文字说明、推理过程或计算步骤.
| 得分 | 阅卷人 |
|
|
|
17.(本小题12分)已知函数![]() (
(![]() 且
且![]() ,
,![]() )
)
(1)判断![]() 的奇偶性;(2)求
的奇偶性;(2)求![]() 反函数。
反函数。
| 得分 | 阅卷人 |
|
|
|
18.(本小题12分)已知函数![]()
(1)求![]() 的值;
的值;
(2)设![]() ,
,![]() ,求
,求![]() 的值。
的值。
| 得分 | 阅卷人 |
|
|
|
19.(本小题12分)设一次函数![]() 的图象关于直线
的图象关于直线![]() 对称的图象为
对称的图象为![]() ,且
,且![]() 。若点
。若点![]() (
(![]() )在曲线
)在曲线![]() 上,并且
上,并且![]() 。(1)求曲线
。(1)求曲线![]() 的方程;(2)求数列
的方程;(2)求数列![]() 的通项公式;
的通项公式;
(3)设![]() ,求
,求![]()
| 得分 | 阅卷人 |
|
|
|
20.(本小题12分)函数![]() 对任意的
对任意的![]() ,
,![]() 都有
都有![]() ,并且当
,并且当![]() 时,
时,![]() 。
。
(1)求证:![]() 是
是![]() 上的增函数;
上的增函数;
(2)若![]() ,解不等式
,解不等式![]() 。
。
| 得分 | 阅卷人 |
|
|
|
21.(本小题13分)已知![]() 是函数
是函数![]() 的一个极值点,其中
的一个极值点,其中![]() ,
,![]() 。
。
(1)求![]() 与
与![]() 的关系表达式;
的关系表达式;
(2)求![]() 的单调区间;
的单调区间;
(3)当![]() 时,函数
时,函数![]() 的图象上任意一点的切线斜率恒大于
的图象上任意一点的切线斜率恒大于![]() ,求
,求![]() 的取值范围。
的取值范围。
| 得分 | 阅卷人 |
|
|
|
22.(本小题13分)对定义域分别为![]() ,
,![]() 的函数
的函数![]() 和
和![]() ,规定
,规定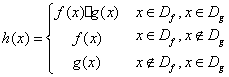
(1)若函数![]() (
(![]() );
);![]() (
(![]() ),写出
),写出![]() 的解析式;
的解析式;
(2)求(1)中![]() 的最大值。
的最大值。
(3)若![]() ,其中
,其中![]() 是常数,且
是常数,且![]() ,请设计一个定义域为
,请设计一个定义域为![]() 的函数
的函数![]() 及一个
及一个![]() 的值,使
的值,使![]() ,并予以证明。
,并予以证明。
攀钢一中2005~2006第一学期中期统一检测试卷参考答案
高 三 数 学(理)
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | A | B | B | B | A | C | D | D | C | D | D |
二、填空题
13.![]() 14.2006 15.
14.2006 15.![]() 16.
16.![]()
三、解答题:本大题6个小题,共74分.解答要写出必要的文字说明、推理过程或计算步骤.
17.解:(1)由![]()
![]()
![]()
∵![]() ,∴
,∴![]() 或
或![]()
∴![]() 的定义域为
的定义域为![]() ,定义域关于原点对称
2分
,定义域关于原点对称
2分
∵![]()
![]() ,即
,即![]()
∴![]() 是奇函数
6分
是奇函数
6分
(2)![]()
![]()
![]()
![]() ∴
∴ ![]() 12分
12分
18.解: ![]()
![]()
![]()
![]()
(1)![]()
![]()
![]() 4分
4分
(2)![]()
∴![]() 6分
6分
![]()
![]()
![]()
![]()
![]() 10分
10分
∵![]() ∴
∴![]() ∴
∴![]() 12分
12分
19.解:(1) 由![]() 是一次函数,可设
是一次函数,可设![]() (
(![]() )
1分
)
1分
∵![]() 的图象关于直线
的图象关于直线![]() 对称的图象为
对称的图象为![]() ,
,
∴图象为![]() 对应函数为
对应函数为![]() 的反函数。
的反函数。
∵点![]() (
(![]() )在曲线
)在曲线![]() 上,并且
上,并且![]() 。
。
∴点![]() 即
即![]() 在曲线
在曲线![]() 上,于是点
上,于是点![]() 在
在![]() 的图象上, 2分
的图象上, 2分
∴![]() ,又
,又![]()
所以![]() ,即
,即![]()
∴曲线![]() 的方程为
的方程为![]() ;
4分
;
4分
(2)∵点![]() 在曲线
在曲线![]() 上,∴
上,∴![]() 6分
6分
∴![]()
![]() 8分
8分
(3)∵![]()
![]()
∴![]()
![]()
![]() 10分
10分
∴![]() 12分
12分
20.解:(1)设![]() 且
且![]() ,则
,则![]() ,∴
,∴![]() 2分
2分
∵对任意的![]() ,
,![]() 都有
都有![]() ,
,
∴![]()
![]() 4分
4分
即![]() ∴
∴![]() 是
是![]() 上的增函数;
6分
上的增函数;
6分
(2)∵![]() ,∴
,∴![]() 8分
8分
由![]() 得
得![]()
∵![]() 是
是![]() 上的增函数
上的增函数
∴![]() 10分
10分
解之得![]()
∴不等式的解集为![]() 12分
12分
21.解:(1)![]()
∵![]() 是函数
是函数![]() 的一个极值点,
的一个极值点,
∴![]()
∴![]() 3分
3分
(2)![]()
![]()
由![]() ,
,![]() 得
得![]() 即
即![]()
由![]() ,
,![]() 得
得![]() 即
即![]() 或
或
∴![]() 的单增区间是
的单增区间是![]() ,单减区间是
,单减区间是![]() ,
,![]() 8分
8分
(3)由已知得![]() 在
在![]() 上恒成立
上恒成立
即![]() ∵
∵![]()
∴![]() ∴
∴![]()
令![]()
∵![]() 在
在![]() 上恒成立
上恒成立
∴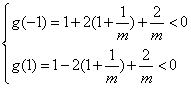
![]()
![]()
∴![]() 的取值范围是:
的取值范围是:![]() 13分
13分
22.解:(1)![]() 4分
4分
(2) 当![]() 时,
时,![]()
![]() ∴
∴![]()
当![]() 时,
时,![]()
∴当![]() 时, h(x)取得最大值是
时, h(x)取得最大值是![]() 8分
8分
(3)令![]() ,
,![]()
则![]()
![]()
于是![]()
![]()
![]() 13分
13分
另解令![]() ,
,![]()
则![]()
![]()
于是![]()
![]()
![]()
