瓯海中学2005学年第一学期高三12月份月考数学试题卷

2014-5-11 0:20:35 下载本试卷

瓯海中学2005学年第一学期高三12月份月考

数学文科试卷

第I卷（选择题，共60分）

一、选择题：本题共有12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一个是正确的，把正确选项的代号填在指定位置上.

1．sin300°的值为（　）

　A． 　　　　　　　B．－ 　　　　 C．　　　　　D．－

2．已知　　（　　）

　　　 A．一个点　　　　　　　 B．　　　　　　　 C．　　　　 D．

3．函数(x>1)的反函数是（　）

A．y=1+log2x (x>1)　　　　　　　　　　　B．y=1+log2x (x>0) 　

C．y=－1+log2x (x>1)　　　　　　　　　　D．y=log2(x－1) (x>1)

4．设，是不共线的向量，=+k(k∈R), =－3+,则A、B、C共线的充

　 要条件是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．k=3　　　　　　　　　　B．k=－3　　　　　　　　 C．k=　　　　　　　　　D．k=－

5．焦点在直线3x－4y－12=0上的抛物线的标准方程为（　）

A．x2=－12y　　　　　　　　　　　　 B．y2=8x或x2=－16y　

C．y2=16x  　　　　　　　　　　　　 D．x2=－12y或y2=16x

6．在正方体ABCD—A1B1C1D1­中，A1C1与AD1所成角为　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．60°　　　　　　　　　 B．90°　　　　　　　　　 C．45°　　　　　　　　　 D．30°

7．若函数上最大值是最小值的3倍，则a=（　　）

　　　 A．　　　　　　　　　 B．　　　　　　　　　 C．　　　　　　　　　　　D．

8．两平行直线l1，l2分别过点P（－1，3），Q（2，－1），它们分别绕P、Q旋转，但始终保持平行，则l1，l2之间的距离的取值范围是　　　　　　　　　　　　　　　　　　　　（ 　 ）

　　　 A．（0，+∞）　　　　B．[0，5]　　　　　　　　 C．　　　　　　　　 D．[0，]

9．已知圆C与圆(x－1)2+y2=1关于直线y=－x+2对称，则圆C的方程为　　　　　　　　（　　）

　　　 A．(x－1)2+y2=1　　　　　　　　　　　　　　　　　　　B．(x+1)2+(y－2)2=1

　　　 C．(x－2)2+(y－1)2=1　　　　　　　　　　　　　　　D．x2+(y－2)2=1

10．已知mn≠0，则方程mx2+ny2=1与mx+ny2=0在同一坐标系下的图象可能是（　）

11．已知P是以F1，F2为焦点的椭圆上的一点，若PF1⊥PF2，

　　tan∠PF1F2=，则此椭圆的离心率为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　　B．　　　　　　　　　　　C．　　　　　　　　　　　D．

12．设A，B，C是△ABC三个内角，且tanA，tanB是方程3x2－5x+1=0的两个实根，那么

　 △ABC是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．钝角三角形　　　　　　　　　　　　　　　　　　　　　 B．锐角三角形

C．等腰直角三角形　　　　　　　　　　　　　　　　 　D．以上均有可能

第Ⅱ卷（非选择题　共90分）

二、填空题：本大题共4小题，每小题4分，共16分.

13．已知向量=(1, 0)，=(2, 2)，则=　　　　　　　 。

14．二次函数上递减，则a的取值范围是　　　  .

15．设双曲线(a>0, b>0)的焦距为2c，A、B分别为实轴与虚轴的一个端点，若坐标原点到直线AB的距离为，则双曲线的离心率为　　　　 ；

16．过直线上一点M向圆作切线，则M到切点的最小距离为　　 ；

文本框: 班级__________________姓名__________________________座号_____________________ …………………………………………装…………………………………………订…………………………………………线………………………………………… 瓯海中学2005学年第一学期高三12月份月考

数学文科答题卷

一、选择题：本题共有12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一个是正确的，把正确选项的代号填在指定位置上.

题号

1

2

3

4

5

6

7

8

9

10

11

12

13

答案

二、填空题：本大题共4小题，每小题4分，共16分.

13．___________________________________　　　　　 14．________________________________

15．___________________________________　　　　　 16．________________________________

三、解答题：本大题共6小题，共74分，解答应写出文字说明证明过程或推演步骤.

17.（本小题满分12分）已知向量a=()，b=()，c=(,－1)，其中x∈R，

（1）当a⊥b时，求x值的集合；

（2）求a－c的最大值。

18．（本小题满分12分）已知数列的前n项和Sn的是n的二次函数，且.

　（1）求Sn的表达式；

　（2）求通项an.

19．（本小题满分12分）已知，且

① 求的最小值；

② 若直线与轴，轴分别交于点A,B,求的面积的最小值。

20．（本小题满分12分）如图，在正三棱住中，各棱长相等，D为BC的中点。求证：

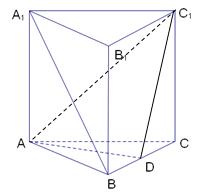（1）；

（2）

21．（本小题满分12分）已知函数在[0，2]上有最小值3，求a的值.

22．（本小题满分14分）已知定点F（1，0），动点P在y轴上运动，过点P作线段PM⊥PF交x轴于M点，延长MP到N，使PN=PM,

（1）求动点N的轨迹C的方程；

（2）直线l与动点N的轨迹C交于A、B两点，若，求直线l的斜率k的取值范围.

瓯海中学2005学年第一学期高三12月份月考

数学（文科）参考答案

1.D　　2.B　 3.A　　4.D　　5.D　 6.A　　7.A　　8.C　　9.C　　10.A　　11.D　12.A

13．　　14．　 15．　 16．

17．解（1）

　　　（2）

18.（1）设

　　　　　 则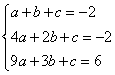………………3分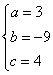　　

　 （2）

　　　　　

19．①，当且仅当即，时取得等号，∴的最小值为。

②设直线：（），则=

而

∴，当且仅当时取得等号，即。

20.(略)

21．解：函数图像的对称轴为　　 分三种情况讨论

　　　 ①当（舍）

　　　 ②当（舍）

　　　 ③

　　　　　 （舍）

　　　　　 综上可知

22．（1）设动点N(x, y)，则M(－x, 0),P(0, ) (x>0)，　　　　　　 （2分）

∵PM⊥PF，∴kPM·kPF=－1，即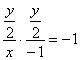　　　　　　 （4分）

∴y2=4x(x>0)即为所求.　　　　　　　　　　　　　　　　  （6分）

　 （2）设直线l方程为y=kx+b , 点A(x1, y1) B(x2, y2), 　　　　　　（7分）

　　　　则由=－4，得x1x2+y1y2=－4,即+y1y2=－4　∴y1y2=－8

由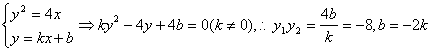（10分）

当△=16－16kb=16(1+2k2)>0时，

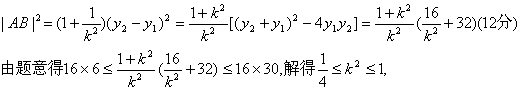　　  ∴≤k≤1，或－1≤k≤－,　　　　　　　　　　　　　　　  （13分）

即所求k的取值范围是.　　　　　　　　　　　 （14分）