南京一中2005-2006学年度第一学期
高三年级期中考试数学试卷
教学班 学号 姓名 得分
一.选择题(本大题共12小题,每小题3分,共36分.每题有且只有一个正确答案,请把正确答案的代号填在答题卡上.)
1.如果命题“p或q”为假命题,则( )
A.p和q均为真命题 B.p和q均为假命题
C.p和q中至少有一个为真命题 D.p和q中至多有一个为真命题
2.在![]() 成立的x取值范围是( )
成立的x取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.函数![]() 的图象不经过( )
的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.设命题甲: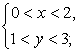 命题乙:
命题乙: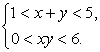 则甲是乙的( )
则甲是乙的( )
A.充分条件,但不是必要条件 B.必要条件,但不是充分条件
C.充要条件 D.既不充分也不必要条件
5.函数![]() 的单调递增区间是( )
的单调递增区间是( )
A、(-1,0![]() B、
B、![]() C、(-∞,0
C、(-∞,0![]() D、
D、![]()
6.不等式![]() 的解集是( )
的解集是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.若函数![]() 的值域为
的值域为![]() ,则函数
,则函数![]() 的值域为( )
的值域为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.一个等比数列![]() 共有2n+1项,奇数项之积为100,偶数项之积为120,则an+1为( )
共有2n+1项,奇数项之积为100,偶数项之积为120,则an+1为( )
A.![]() B.
B.![]() C.20 D.110
C.20 D.110
9.已知函数![]() 的最大值是
的最大值是![]() ,则实数a的取值范围是( )
,则实数a的取值范围是( )
A.0≤a≤1 B.0≤a≤2 C.-2≤a≤0 D.-1≤a≤0
10.设![]() 是等差数列
是等差数列![]() 的前
的前![]() 项和,若
项和,若![]() ,则
,则![]() =(
)
=(
)
A.1 B.![]() C.2 D.
C.2 D.![]()
11.已知平面上直线![]() 的方向向量
的方向向量![]() ,点
,点![]()
![]() 和
和![]()
![]() 在
在![]() 上的射影分别是
上的射影分别是![]() 和
和![]() ,则
,则![]() ,其中
,其中![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.定义在![]() 上的函数
上的函数![]() 满足
满足![]() ,当
,当![]() 时,
时,![]() ,则( )
,则( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二.填空题(本大题共有5个小题,每小题4分,共20分,请把正确答题的结果填在题中横线上)
13.已知函数f(x2)=2![]() ,则
,则![]() = .
= .
14.已知![]() ,
,![]() 是非零向量且满足
是非零向量且满足![]() ,
,![]() ,则
,则![]() 与
与![]() 夹角为____________.
夹角为____________.
15.已知数列![]() ,
,![]()
![]() 且数列
且数列![]() 的前n项和
的前n项和![]() ,那么n的值为 .
,那么n的值为 .
16.设函数![]() (
(![]() )为奇函数,
)为奇函数,![]() ,
,![]() ,则
,则![]() .
.
17.给出以下命题:
①存在实数x,使得sin x+cos x=![]() ,
,
②若α,β是第一象限角,且α>β,则cos α<cos β,
③函数y=![]() 是偶函数,
是偶函数,
④将y=sin 2x的图象向左平移![]() 个单位得到的是y=sin
个单位得到的是y=sin![]() .
.
其中正确命题的序号是 .(把你认为正确的命题的序号填在横线上)
三.解答题(本大题共有5个小题,第18、19、20题每题8分,其余小题每题10分,共44分,要求写出必要的解答过程)
18.已知![]() 的值.
的值.
19.已知函数![]() ,且
,且![]() 、
、![]() 、
、![]() 成等差数列.若
成等差数列.若![]() 、
、![]() 、
、![]() 是两两不相等的正数,且
是两两不相等的正数,且![]() 、
、![]() 、
、![]() 成等比数列,试判断
成等比数列,试判断![]() 与
与![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
20.已知二次函数![]() 设方程
设方程![]() 的两实根为
的两实根为![]()
(1)求证:![]() ;
;
(2)若![]() 的图像的对称轴是
的图像的对称轴是![]() ;
;
21.如图,在![]() △ABC中,已知
△ABC中,已知![]() .若长为
.若长为![]() 的线段
的线段![]() 以点A为中点,问
以点A为中点,问![]() 与
与![]() 的夹角
的夹角![]() 取何值时
取何值时![]() 的值最大?并求出这个最大值。
的值最大?并求出这个最大值。
 |
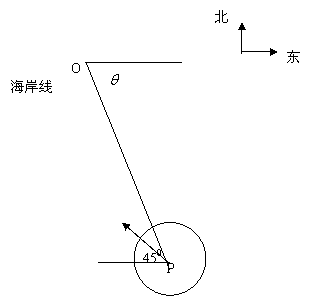
 22.某海滨城市附近海面有一台风,据监测,当前台风中心位于城市
22.某海滨城市附近海面有一台风,据监测,当前台风中心位于城市![]() (如图)的东偏南
(如图)的东偏南![]() (
(![]() 方向300千米的海面
方向300千米的海面![]() 处,并以20千米/时的速度向西偏北
处,并以20千米/时的速度向西偏北![]() 方向移动。台风侵袭的范围为圆形区域,当前半径为60千米,并以10千米/时的速度不断增大。问几小时后该城市开始受到台风的侵袭?
方向移动。台风侵袭的范围为圆形区域,当前半径为60千米,并以10千米/时的速度不断增大。问几小时后该城市开始受到台风的侵袭?
 |
参考答案:
一、选择题
1、B 2、C 3、A 4、A 5、B 6、B 7、C 8、B 9、A 10、A 11、D 12、D
二、填空题
13、2 14、![]() 15、99 16、
15、99 16、![]() 17、③
17、③
三、解答题
18、解:![]()
![]()
19、解:由于函数![]() ,且
,且![]() 、
、![]() 、
、![]() 成等差数列
成等差数列
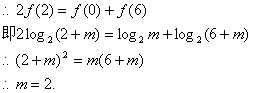
又![]() 、
、![]() 、
、![]() 是两两不相等的正数,且
是两两不相等的正数,且![]() 、
、![]() 、
、![]() 成等比数列
成等比数列
![]()
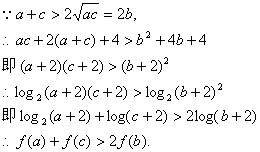
20、解:(1)因为二次函数![]() 方程
方程![]() 的两实根为
的两实根为![]()
所以![]()
(2)![]()
令![]()
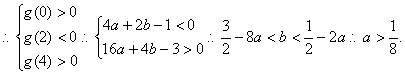
![]() 。
。
又![]() 对称轴
对称轴![]() .
.
所以![]()
21、设│AB│=c,│AC│=b,则A(0,0),B(c,0),C(0,b),且│PQ│=2a,
│BC│=a.
设点P的坐标为(x,y),则Q(-x,-y)
∴![]() ,
,![]() ,
,![]() ,
,![]()
∴![]()
∵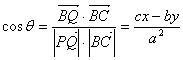
∴![]()
∴![]()
故当![]()
![]() ,即
,即![]() (
(![]() 与
与![]() 方向相同)时,
方向相同)时,![]() 最大,其最大值为0
最大,其最大值为0
22、解:设在时刻![]() (时)台风中心为
(时)台风中心为![]() ,此时台风侵袭的圆形区域半径为
,此时台风侵袭的圆形区域半径为![]() (千米)。
(千米)。
若在时刻![]() 城市
城市![]() 受到台风的侵袭,则
受到台风的侵袭,则![]() 。
。
由余弦定理知![]()
由于![]() ,
,![]() ,
,
![]()
![]() ,
,
故![]()
因此![]() ,即
,即![]() ,解得
,解得![]()
答:12小时后该城市开始受到台风的侵袭。