天津一中2005-2006-1高三年级第二次月考数学(理)试卷
考号____________班级_________ 姓名__________ 成绩__________
一.选择题:(每题5分,共60分)
1.在等比数列![]() 中,
中,![]() ,则
,则![]() 等于( )
等于( )
A.27 B.-27 C.81或-36 D.27或-27
2.设集合![]() ,则
,则![]() 为( )
为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.“![]() ”是“
”是“![]() ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.函数![]() 的定义域是
的定义域是![]() ,则其值域为( )
,则其值域为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
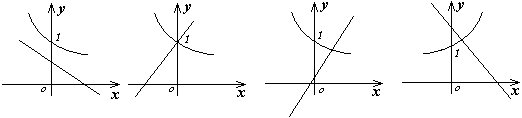 5.当
5.当![]() 时,函数
时,函数![]() 和
和![]() 的图象只可能是( )
的图象只可能是( )
A. B. C. D.
6.函数![]() 的反函数的图象经过点(4,2),则
的反函数的图象经过点(4,2),则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.2 D.4
C.2 D.4
7.下列同时满足条件(1)是奇函数(2)在[0,1]上是增函数(3)在[0,1]上最小值为0的函数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知数列![]() 的通项公式为
的通项公式为![]() ,设其前n项和为Sn,则使Sn<-5成立的自然数n( )
,设其前n项和为Sn,则使Sn<-5成立的自然数n( )
 A.有最小值63 B.有最大值63 C.有最小值31 D.有最大值31
A.有最小值63 B.有最大值63 C.有最小值31 D.有最大值31
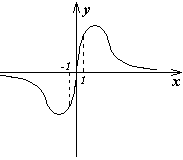
9.若函数![]() 的图象如图所示,则m的范围为( )
的图象如图所示,则m的范围为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.复数![]() 在复平面内对应的点不可能位于( )
在复平面内对应的点不可能位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11.三个数a,b,c成等比数列,且![]() ,则b的取值范围是( )
,则b的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.已知![]() 的定义域为R,对任意
的定义域为R,对任意![]() ,有
,有![]() ,且
,且![]() ,
,![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二.填空题:(每题4分,共16分)
13.关于x的方程![]() 有三个不相等的实数根,则实数a的取值为________.
有三个不相等的实数根,则实数a的取值为________.
14.等差数列![]() 中,
中,![]() ,若
,若![]() 且
且![]() ,则m的取值为____________.
,则m的取值为____________.
15.数列![]() 中,
中,![]() ,Sn是前n项和,当
,Sn是前n项和,当![]() 时,
时,![]() ,则
,则![]() _______.
_______.
16.某种电热水器的水箱盛满水是200升,加热到一定温度后可洗浴。洗浴时,已知每分钟放水34升,在放水的同时注水,t分钟注水![]() 升,当水箱内水量达到最小值时,放水自动停止,现假定每人洗浴用水65升,则该热水器一次至多可供____________人洗浴.
升,当水箱内水量达到最小值时,放水自动停止,现假定每人洗浴用水65升,则该热水器一次至多可供____________人洗浴.
三.计算题:(17~21题每题12分,第22题14分)
17.两个人射击,甲射击一次中靶概率为p1,乙射击一次中靶概率是p2,已知![]() 是方程
是方程![]() 的两个实根,若两人各射击5次,甲中靶次数的方差为
的两个实根,若两人各射击5次,甲中靶次数的方差为![]() ,乙中靶次数的方差为
,乙中靶次数的方差为![]() .(1)求p1和p2.(2)两人各射击2次,中靶至少3次就算完成任务,求完成任务的概率是多少?
.(1)求p1和p2.(2)两人各射击2次,中靶至少3次就算完成任务,求完成任务的概率是多少?
18.已知数列![]() 的前n项和Sn=9-6n.
的前n项和Sn=9-6n.
(1)求数列![]() 的通项公式.
(2)设
的通项公式.
(2)设![]() ,求数列
,求数列![]() 的前n项和.
的前n项和.
19.设命题p:函数![]() 的定义域为R;命题q:不等式
的定义域为R;命题q:不等式![]() 对一切
对一切![]() 均成立,如果命题“p或q”为真命题,命题“p且q”为假命题,求实数a的取值范围.
均成立,如果命题“p或q”为真命题,命题“p且q”为假命题,求实数a的取值范围.
20.定义在R上的函数![]() ,当
,当![]() 时
时![]() ,且对任意
,且对任意![]() ,都有
,都有![]() .
.
(1)证明:![]()
(2)证明:对任意![]() ,恒有
,恒有![]() .
.
(3)证明:![]() 是R上的增函数.
是R上的增函数.
(4)若![]() ,求x的取值范围.
,求x的取值范围.
21.已知集合M是满足下列性质的函数![]() 的全体:存在非零常数k,对任意
的全体:存在非零常数k,对任意![]() (D为函数的定义域),等式
(D为函数的定义域),等式![]() 成立.
成立.
(1)一次函数![]() 是否属于集合M?说明理由.
是否属于集合M?说明理由.
(2)设函数![]() 的图象与直线y=x有公共点,试证明:
的图象与直线y=x有公共点,试证明:![]() .
.
天津一中2004-2005-1高三年级第二次月考数学(理)试卷答案
一.选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | D | A | A | C | B | B | A | C | A | D | D |
二.填空题:
13.![]() 14.10 15.
14.10 15.![]() 16.4
16.4
三.计算题:
17.解:(1)![]() 二根为2,3
二根为2,3
∴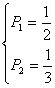 或
或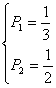
设甲、乙射击5次,中靶次数分别为![]()
则![]() 满足
满足
![]() 满足
满足
∴![]()
(2)![]()
18.解:(1)![]() 时,
时,![]()
∴![]()
![]() 时,
时,![]()
∴![]()
∴通项公式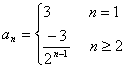
(2)当![]() 时,
时,![]() ∴
∴![]()
![]() 时,
时,![]() ∴
∴![]()
∴![]()
![]()
19.解:p为真 ![]() 恒成立
恒成立
![]() 时
时![]() 恒成立 或
恒成立 或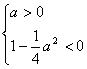
![]()
q为真 ![]() 对
对![]() 恒成立
恒成立
![]()
而![]() 在x>0时单调递减
在x>0时单调递减
∴![]()
∴![]()
即q为真![]()
∵“p或q”为真,“p且q”为假
∴p真q假时,a>2且a<1 即a不存在
p假q真时,![]()
∴a的取值范围为[1,2]
20.证明:(1)令a=b=0,得![]()
又![]() , ∴
, ∴![]()
(2)任取![]() ∴
∴![]()
又![]()
∴![]()
又由已知x>0时![]()
∴对任意![]() 恒成立
恒成立
(3)任取x1<x2总有
![]()
∵![]() ∴
∴![]()
∴![]()
∴![]() 在R上递增
在R上递增
(4)原不等式化为![]()
∴![]() 得
得![]()
21.解:(1)若一次函数![]() ,则存在
,则存在![]() ,
,
使![]() 即
即![]() (*)成立
(*)成立
显然对任意![]() ,(*)不恒成立 ∴
,(*)不恒成立 ∴![]()
(2)若![]()
须且只须存在![]() 使
使![]()
也即![]() 对任意x>0恒成立
对任意x>0恒成立
∵![]() 与
与![]() 有交点
有交点
∴![]() 必与
必与![]() 有交点
有交点![]()
显然![]() ∴k存在,k=x0
∴k存在,k=x0
22.解:(1)![]()
![]() ①
①
又∵![]() 区性
②
区性
②
由①②得 ![]()
![]()
得![]() 代入
代入
整理得:![]()
![]()
∵![]() ∴
∴![]()
(2)由![]() 变形为
变形为![]()
∴![]() 为首项为
为首项为![]() ,公比为
,公比为![]() 的等比数列
的等比数列
![]()
∴![]()
(3)![]() 时,
时,![]() ∴
∴![]()
∴![]()
22.由坐标原点O向曲线![]() 引切线,切于O以外的点P1(x1,y1),再由P1作此曲线的切线,切于P1以外的点P2(x2,y2),如此进行下去,得到点列
引切线,切于O以外的点P1(x1,y1),再由P1作此曲线的切线,切于P1以外的点P2(x2,y2),如此进行下去,得到点列
{Pn(xn,yn)},求:
(1)xn与xn-1(n≥2)的关系式.
(2)数列{xn}的通项公式.
(3)当![]() 时,Pn的极限位置的坐标.
时,Pn的极限位置的坐标.
