惠州市2006届高三第二次调研考试
数学试题(2006.1)
本试卷分第1卷(选择题)和第2卷(非选择题)两部分,满分150分,考试时间120分钟.
第1卷(选择题,共50分)
一、选择题:每小题5分,共50分.
1.若集合M=![]() xx<1
xx<1![]() ,N=
,N=![]() xx2<1
xx2<1![]() ,则M∩N=( )
,则M∩N=( )
A.M B.N
C.![]() D.
D.![]() x-1<x<0
x-1<x<0![]()
![]()
![]() x0<x<1
x0<x<1![]()
2.设复数ω=![]() ,则1+ω=( )
,则1+ω=( )
A.-ω B.ω2 C.-![]() D.
D.![]()
3.直线y=kx与圆 (x-4)2+y2=4相切,则直线的倾斜角为( )
A.![]() ,-
,-![]() B.
B.![]() ,
,![]() C.
C.![]() ,-
,-![]() D.
D.![]() ,
,![]()
4.甲、乙两棉农,统计连续五年的面积产量(千克∕亩)如下表:
| 棉农甲 | 68 | 72 | 70 | 69 | 71 |
| 棉农乙 | 69 | 71 | 68 | 68 | 69 |
则平均产量较高与产量较稳定的分别是( )
A.棉农甲,棉农甲 B.棉农甲,棉农乙
C.棉农乙,棉农甲 D.棉农乙,棉农乙
5.已知△![]() 中,
中,![]() =3,
=3,![]() =4,且
=4,且![]() ·
·![]() =-6
=-6![]() ,则△
,则△![]() 的面积是( )
的面积是( )
A.6 B.3![]() C.3 D.
C.3 D.![]()
6.在正方体ABCD-A1B1C1D1中,E为AA1的中点,点P在其对角面BDD1D内运动,若EP总与直线AC成等角,则点P的轨迹有可能是( )
A.圆或圆的一部分 B.抛物线或其一部分
C.双曲线或其一部分 D.椭圆或其一部分
7.在等比数列{an}中,a1+a2=162,a3+a4=18,a4+a5=( )
A.6 B.-6 C.±2 D.±6
8.函数f (x)=![]() 满足f (9)=2,则
满足f (9)=2,则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.2 D.
C.2 D.![]()
9.已知双曲线![]() 的右焦点为F,右准线与一条渐近线交于点A,
的右焦点为F,右准线与一条渐近线交于点A,
△OAF的面积为![]() (O为原点),则两条渐近线的夹角为( )
(O为原点),则两条渐近线的夹角为( )
A.30° B.45° C.60° D.90°
10.若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“孪生函数”,那么函数解析式为y=2x2+1,值域为{5,19}的“孪生函数”共有( )
A.10个 B.9个 C.8个 D.7个
第2卷(非选择题,共100分)
二、填空题:每小题5分,共20分.
11.cos70°cos10°+sin70°sin10°=______________.
12.一个距球心距离为1的平面截球所得的圆的面积为π,则球的半径为_______(3分),球的表面积为______________.(2分)
13.若函数f (x)满足f (a+b)=f (a)·f (b),且f (1)=2,则![]()
______________.
14.已知实数a,b满足等式log2a=log3b,给出下列5个关系式:①a>b>1;②b>a>1;③a<b<1;④b<a<1;⑤a=b.其中可能成立的关系式是____________.(填序号)
三、解答题:本大题共6小题,共80分.
15.(本小题满分12分)
已知函数![]() (a
(a![]() R,a为常数) .
R,a为常数) .
(1)求函数![]() 的最小正周期;
的最小正周期;
(2)若函数![]() 在[
在[![]() ,
,![]() ]上的最小值为-1,求实数a的值.
]上的最小值为-1,求实数a的值.
16.(本小题满分12分)
已知数列![]() 为等差数列,且
为等差数列,且![]() ,
,![]() .
.
(1)求数列![]() 的通项公式
的通项公式![]() ;
;
(2)求![]() …
…![]() 的值.
的值.
17.(本小题满分14分)
某次有奖竞猜活动中,主持人准备了A、B两个相互独立的题目,并且宣布:观众答对问题A可获奖金a元,答对问题B可获金2a元;先答那个题目由观众自由选择;只有第1个问题答对,才能再答第2个问题,否则中此答题.若你被选为幸运观众,且假设你答对问题A、B的概率为![]() 、
、![]() ,你觉得应先回答哪个问题才能使你获得奖金的期望较大?说明理由.
,你觉得应先回答哪个问题才能使你获得奖金的期望较大?说明理由.
18.(本小题满分14分)
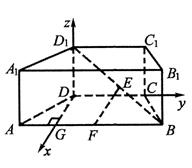 如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2AD=2DC=2,E为BD1的中点,F为AB的中点.
如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2AD=2DC=2,E为BD1的中点,F为AB的中点.
(1)求证:EF⊥平面ADD1 A1;
(2)建立空间直角坐标系D-xyz (DG是AB边上的高),
若BB1=![]() ,求A1F与平面DEF所成的角的大小.
,求A1F与平面DEF所成的角的大小.
19.(本小题满分14分)
已知函数![]() .
.
(1)如果关于![]() 的不等式
的不等式![]() ≥
≥![]() 的解集为R,求实数a的最大值;
的解集为R,求实数a的最大值;
(2)设函数![]() ,如果
,如果![]() 在区间(0,1)上存在极小值,求实数a的取值范围.
在区间(0,1)上存在极小值,求实数a的取值范围.
20.(本小题满分14分)
定义:离心率![]() 的椭圆为“黄金椭圆”.已知椭圆E:
的椭圆为“黄金椭圆”.已知椭圆E:![]() 的一个焦点为F (c,0) ( c>0),P为椭圆E上的任意一点.
的一个焦点为F (c,0) ( c>0),P为椭圆E上的任意一点.
(1)试证:若a,b,c不是等比数列,则E一定不是“黄金椭圆”;
(2)设E为“黄金椭圆”,问:是否存在过点F、P的直线L与y轴的交点R满足![]() ?若存在,求直线L的斜率k;若不存在,说明理由.
?若存在,求直线L的斜率k;若不存在,说明理由.
(3)已知椭圆E的短轴长是2,点S (0,2),求使![]() 取最大值时点P的坐标.
取最大值时点P的坐标.